文章转自微信公众号:机器学习炼丹术
笔记:陈亦新
我个人的理解:PCA本质上就是寻找数据的主成分。我们可以简单的打个比方,假设有一组高维数据。他的主成分方向就是用一个线性回归拟合这些高维数据的方向。用最小二乘的逻辑拟合的。其他的主成分都是与最大主成分正交的。
那么我们如何得到这些包含主成分方向呢?
通过计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值和特征向量,选择特征值最大的k个特征对应的特征向量组成的矩阵就可以了。这个矩阵就可以将原始m维度的特征转换成k维度。
那么我们如何得到数据的特征向量呢?
一般有两种方法:
特征值分解协方差矩阵
奇异值分解协方差矩阵。
所以PCA算法有两种实现,分别是基于特征值分解方差矩阵实现PCA、基于SVD分解的协方差矩阵PCA算法。
协方差矩阵和散度矩阵
样本均值:
样本方差:
样本X和样本Y(X和Y是两个变量)的协方差:
从上面公式可以得到以下结论:
协方差是在两个变量间计算的,方差可以看成协方差的特征情况
方差和协方差除以了n-1,这是得到方差和协方差的无偏估计。
协方差大于0,X和Y为正相关关系,小于0就是负相关,等于0就是相互独立。
当现在有N个变量,我们要计算这n个变量的彼此两两的协方差的时候,就构成了协方差矩阵。对于三个变量XYZ:
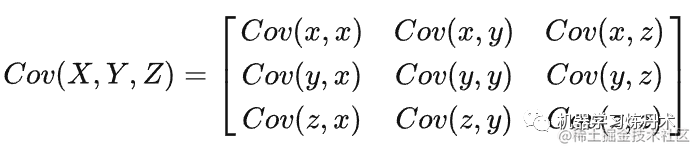
现在我们来看散度矩阵的定义。
❝the scatter matrix is computed by the following equation:
需要注意的是,散度矩阵和协方差矩阵其实就是倍数关系(n-1)倍。散度矩阵的写法是矩阵的写法,和协方差矩阵公式其实等价。
公式中的n是样本数量
对于每一个样本,我们可以假设每一个样本都包含n个特征,也就是每一个样本都是m维度数据。
所以最后可以得到一个mxm的矩阵,分别表示每一个特征和其他的特征的协方差(散度)
写成矩阵的形式,假设是mxn的张量,那么散度矩阵可以写成
散度矩阵和协方差矩阵的特征值和特征向量是一样的。
特征值分解矩阵原理
特征值分解和奇异值分解在机器学习中都是很常见的矩阵分解算法。两者有着很紧密的关系,目的都是提取出矩阵的最重要的特征。
如果一个向量v是矩阵A的特征向量,那么一定可以表示成下面的形式:
其中是特征向量v对应的特征值,一个矩阵的特征向量彼此正交。
这时候问题来了:为什么一个向量和矩阵相乘的结果和一个数字相乘的效果一样呢?
因为矩阵A和向量b相乘,就是对向量v进行了一次线性的变换,旋转、拉伸等等。如果改变换等价于一个常熟的倍数变换,那么就以位置,我们求取特征向量的时候,就是为了求矩阵A可以使得那些哪些向量只发生伸缩变换,不发生旋转变换。
我们来看特征值和特征向量的几何意义
参考资料:机器学习中SVD总结 (qq.com)
一个矩阵其实就是一次线性比那换,因为矩阵乘以一个向量后得到的向量,就相当于是将这个向量进行了线性变换,比方说下面这个矩阵
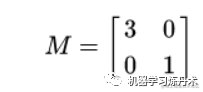
自己可以尝试一下,其实就是让x方向变成原来的3倍,y方向是原来的1倍:
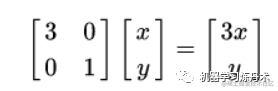
所以是这个样子的:
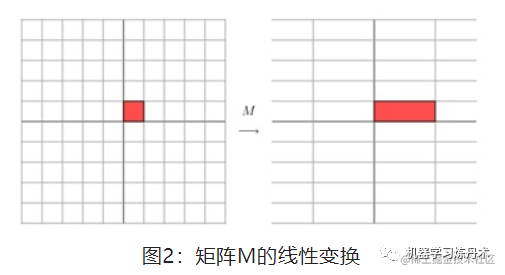
同理,这样的矩阵是一个拉伸变换:
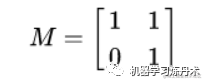
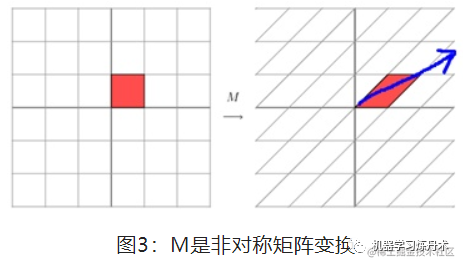
现在我们知道了,矩阵对于一个向量来说,就是一种线性变换。特征值分解就是将矩阵A分解成下面的样子:
Q是矩阵A的特征向量组成的矩阵,是一个对角矩阵,对角线上的元素就是特征值。分解的这个矩阵是一个对角矩阵,里面的特征值是从大到小排列的。
上面公式怎么来的呢?其实就是从特征值的定义得到的。
展示的是单个特征向量的变化。假设矩阵A是mxm的方针。那么v就是一个mx1的某一个特征向量。如果我们对所有的m个特征向量都做这个运算,那么就可以写成:
这里需要反过来,自己举一个例子就可以发现,需要反过来。
然后我们把左边的V变成右边的可逆形式就可以了。
奇异值分解
特征值分解只能针对方针,如果A是一个非方阵,尤其是在PCA当中,样本的特征数量和样本数量一般都是不相同的。这时候就无法使用特征值分解的方法来计算特征向量。
SVD,singular value decomposition
定义
对于任意矩阵A总是存在一个奇异值分解:
假设A是一个mn的矩阵,那么U是一个mm的仿真,U的正交向量(特征向量)被称为左奇异向量,是一个mn的矩阵,是一个对角矩阵,对角线上的元素称为奇异值。是一个nn的矩阵,里面的正交向量被称为右奇异向量。
需要注意的是:
与特征值分解类似,U和V都是正交矩阵,也就是理解为特征向量拼成的矩阵;
那么我们如何计算奇异值和奇异向量呢?还得回到特征向量的定义当中。
这里的v就是右奇异向量,也就是说就是
更有趣的是:
这里的u就是左奇异向量,也就是说就是
为什么有这样的效果呢?
这里单位矩阵,因为U是正交矩阵。
所以上证明了的特征向量,就是我们的V,矩阵V就是ATA的特征向量,那么就是矩阵V的特征值。从上公式中可以看到,奇异值就是特征值的0.5次方。
总结:现在我们已经知道用奇异值分解SVD来处理任何的矩阵了。也就是说,任何的矩阵都可以被分解的形式。
那么SVD降维,就是选择最大的几个奇异值和奇异向量来描述数据就可以了。因为奇异值的下降速度非常快,可能最大的1%的奇异值就已经占据了全部奇异值之和的99%以上
PCA
现在我们了解了特征值分解和奇异值分解。
【基于特征值分解协方差矩阵实现PCA】
去平均值,每一个特征都要预处理,变成0均值分布
计算协方差矩阵或者散度矩阵,就是
用特征值分解求协方差矩阵的特征值和特征向量
选择最大的k个特征值的特征向量,组成一个特征向量矩阵P,这个矩阵的形状为mxk的,m是原来样本特征维度,也是协方差矩阵(方阵)的维度。
每一个数据都包含m个特征,堪称是1xm的向量,与mxk的特征向量做乘法就可以得到1xk的压缩特征。
本质就是选择k中加权方案,每一个方案都是对原来m个特征进行线性加权组合,唯一的限制就是加权方案彼此正交。
【基于SVD分解的协方差矩阵实现PCA】 其实流程和上面是一样的,计算协方差矩阵,通过SVD计算特征值和特征向量(奇异向量)
区别在于,PCA在特征值分解中,需要计算出协方差矩阵的k个最大特征向量。计算协方差矩阵的时候其实计算量非常大,比方说有上万个数据,每个数据有上万个特征。假设都是1w样本和1w特征,那么kxn与nxk两个矩阵结果得到一个10000x10000的协方差矩阵,这个矩阵的每一个元素都需要经过10000次乘法运算,所以需要1万亿次的计算。
SVD来做分解的时候,SVD的实现算法有一些可以不求出协方差矩阵,在不求的情况下,也可以求出我们的左奇异矩阵U。实际上scikit-learn的PCA算法背后就是用SVD实现的,而不是特征值分解。
左右奇异矩阵都可以作为降维的矩阵使用。两者分别降维样本矩阵的两个维度,一个是特征,也就是我们常用的左奇异矩阵;另一个是降低样本数量,是用的右奇异矩阵。
python代码
用特征值分解的方法,把6个样本2个特征转化为1个特征:
##Python实现PCA
import numpy as np
def pca(X,k):#k is the components you want
#mean of each feature
n_samples, n_features = X.shape
mean=np.array([np.mean(X[:,i]) for i in range(n_features)])
#normalization
norm_X=X-mean
#scatter matrix
scatter_matrix=np.dot(np.transpose(norm_X),norm_X)
#Calculate the eigenvectors and eigenvalues
eig_val, eig_vec = np.linalg.eig(scatter_matrix)
eig_pairs = [(np.abs(eig_val[i]), eig_vec[:,i]) for i in range(n_features)]
# sort eig_vec based on eig_val from highest to lowest
eig_pairs.sort(reverse=True)
# select the top k eig_vec
feature=np.array([ele[1] for ele in eig_pairs[:k]])
#get new data
data=np.dot(norm_X,np.transpose(feature))
return data
X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
print(pca(X,1))结果:
用scikit-learn的方法:
from sklearn.decomposition import PCA
import numpy as np
X = np.array([[-1,1],[-2,-1],[-3,-2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=1)
pca.fit(X)
print(pca.transform(X))结果:


往期精彩回顾
适合初学者入门人工智能的路线及资料下载(图文+视频)机器学习入门系列下载机器学习及深度学习笔记等资料打印《统计学习方法》的代码复现专辑机器学习交流qq群955171419,加入微信群请扫码最后
以上就是开放流沙最近收集整理的关于【机器学习】PCA、SVD深入浅出与python代码的全部内容,更多相关【机器学习】PCA、SVD深入浅出与python代码内容请搜索靠谱客的其他文章。









发表评论 取消回复