文章目录
- 前言
- 数据降维的作用
- 一、主成分分析(PCA)
- 1.介绍
- 2.算法流程
- 3.主成分分析的说明
- 二、因子分析(FA)
- 1.介绍
- 2.算法流程
- 3.因子分析和主成分分析的对比
- 三、典型相关性分析(CCA)
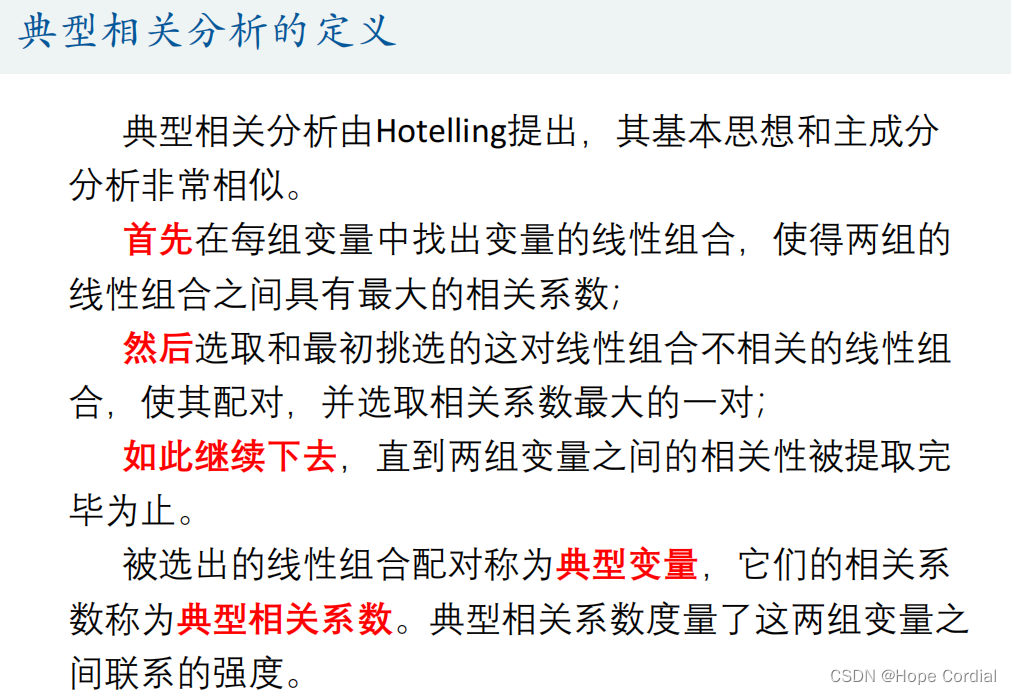
- 1.介绍
- 2.算法思路
- 3.算法流程
- 总结
前言
这里介绍三种降维算法,先介绍一下各自的特点。主成分分析主要是吧多个指标进行降维,只保留几个指标;因子分析要优于主成分分析,那为什么这么说呢?因为因子分析比主成分分析好解释,主成分分析使用后不好解释,因子分析作用与主成分分析相同;典型相关性分析的作用感觉有些局限(相比于以上两种算法),典型相关分析是研究两组变量之间相关关系的一种多元统计方法,它能够揭示出两组变量之间的内在联系,就是说在分别包含多个指标的两组数据中分别挑选出一个指标来代替自己那一组的数据,以此来进行分析两组数据的联系。
数据降维的作用
- 降维是将高维度的数据(指标太多)保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。
- 在实际的生产和应用中,降维在一定的信息损失范围内,可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。
降维具有如下一些优点:
- 使得数据集更易使用;
- 降低算法的计算开销;
- 去除噪声;
- 使得结果容易理解。

一、主成分分析(PCA)
1.介绍
主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说,当研究的问题涉及到多变量且变量之间存在很强的相关性时,我们可考虑使用主成分分析的方法来对数据进行简化。
主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法。从数学角度来看,这是一种降维处理技术。
2.算法流程
- 进行标准化处理
- 计算标准化样本的协方差矩阵
- 计算R的特征值和特征向量
- 计算主成分贡献率以及累计贡献率
- 写出主成分
- 根据系数分析主成分代表的含义
- 利用主成分的结果进行后续的分析




3.主成分分析的说明

因为因子分析比主成分分析容易解释,使用因子分析是比主成分分析更好的降维的方法。
二、因子分析(FA)
1.介绍
- 因子分析由斯皮尔曼在1904年首次提出,其在某种程度上可以被看成是主成分分析的推广和扩展。
- 因子分析法通过研究变量间的相关系数矩阵,把这些变量间错综复杂的关系归结成少数几个综合因子,由于归结出的因子个数少于原始变量的个数,但是它们又包含原始变量的信息,所以,这一分析过程也称为降维。由于因子往往比主成分更易得到解释,故因子分析比主成分分析更容易成功,从而有更广泛的应用。
阅读博客:因子分析全流程汇总
2.算法流程
-
KMO 和 Bartlett 的检验

注意:用SPSS做因子分析时,在查看器中若得不到 KMO检验和 Bartlett检验结果,则说明你的样本量小于指标数了,需要增加样本量或者减少指标个数再来进行因子分析。 -
方差解释率表格
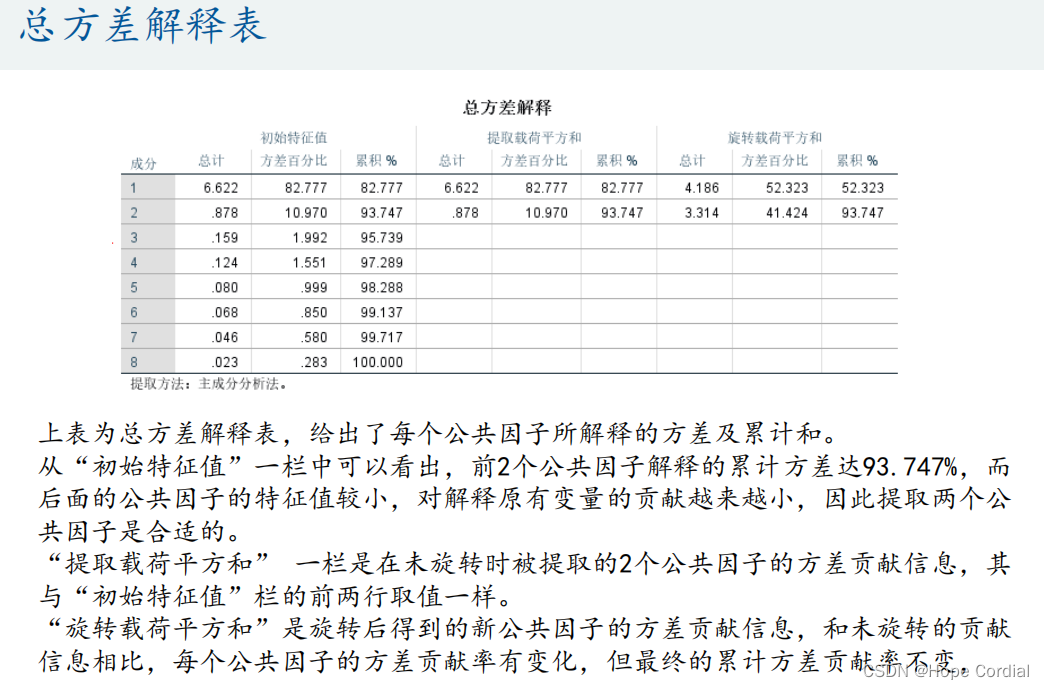
-
旋转后因子载荷系数表格
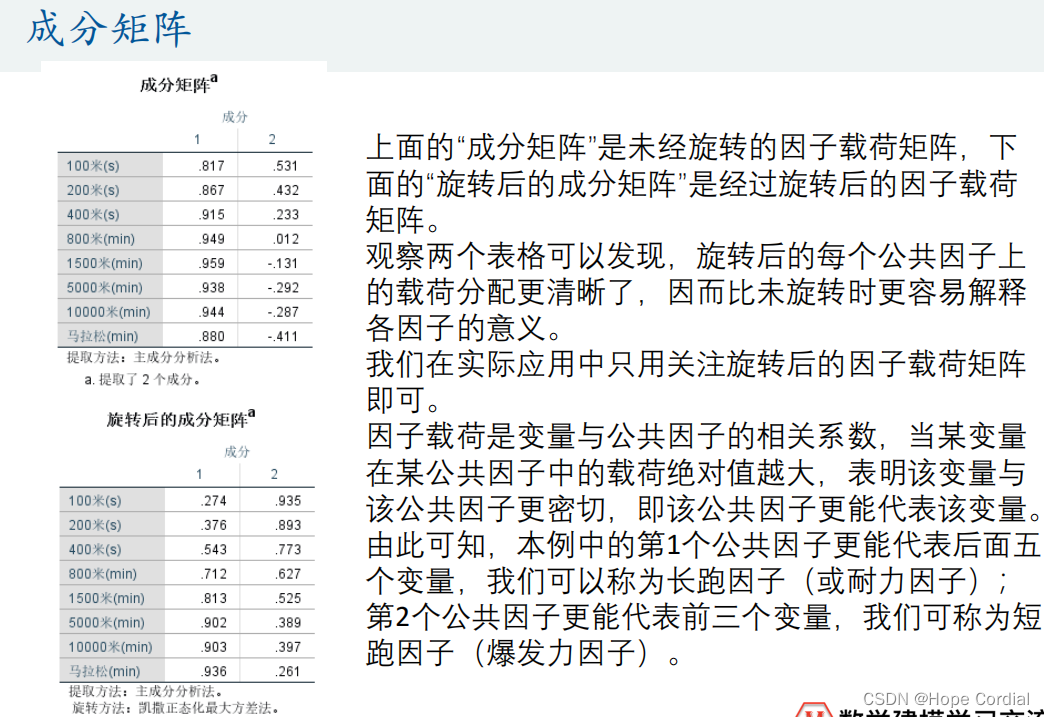
-
碎石图
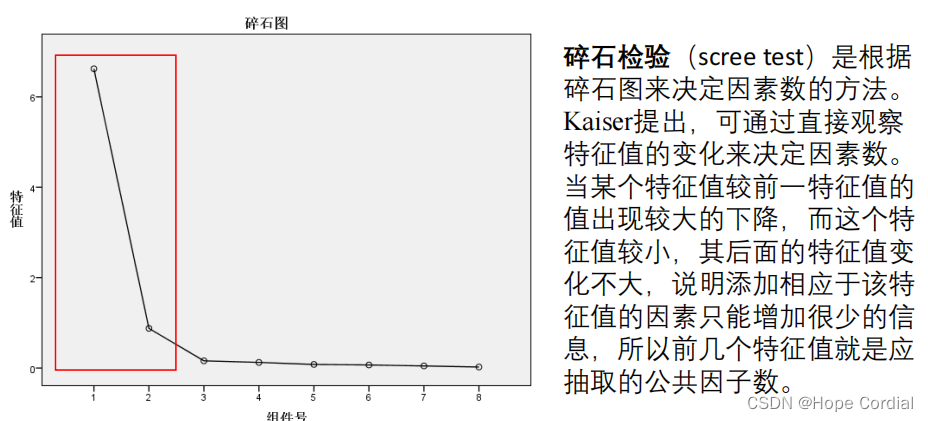
-
补充说明:因子计算权重
-
成分得分系数矩阵
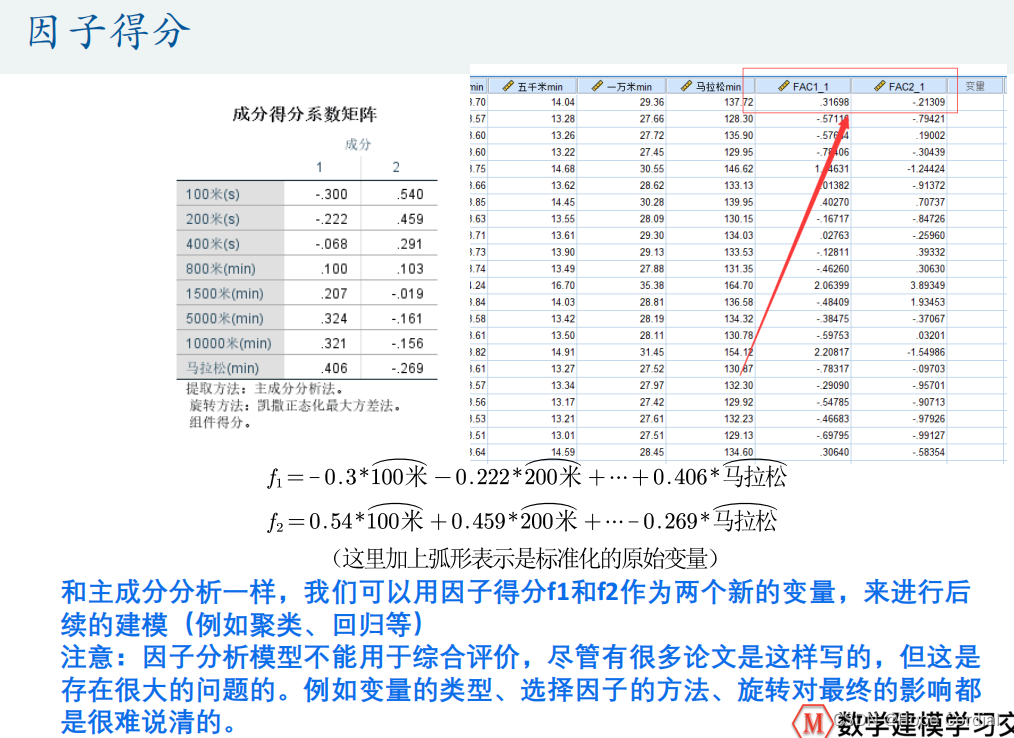
-
载荷图
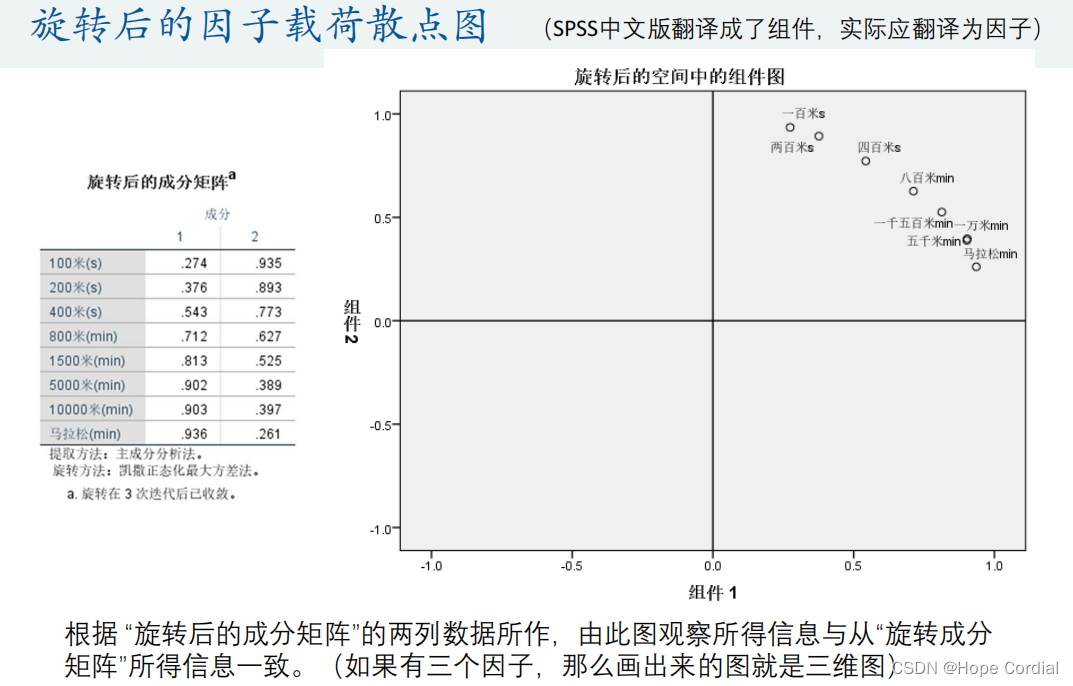
-
线性组合系数及权重结果
3.因子分析和主成分分析的对比

三、典型相关性分析(CCA)
1.介绍
研究两组变量(每组变量中都可能有多个指标)之间相关关系的一种多元统计方法。它能够揭示出两组变量之间的内在联系。即把多个变量与多个变量之间的相关化为两个具有代表性的变量之间的相关。
2.算法思路
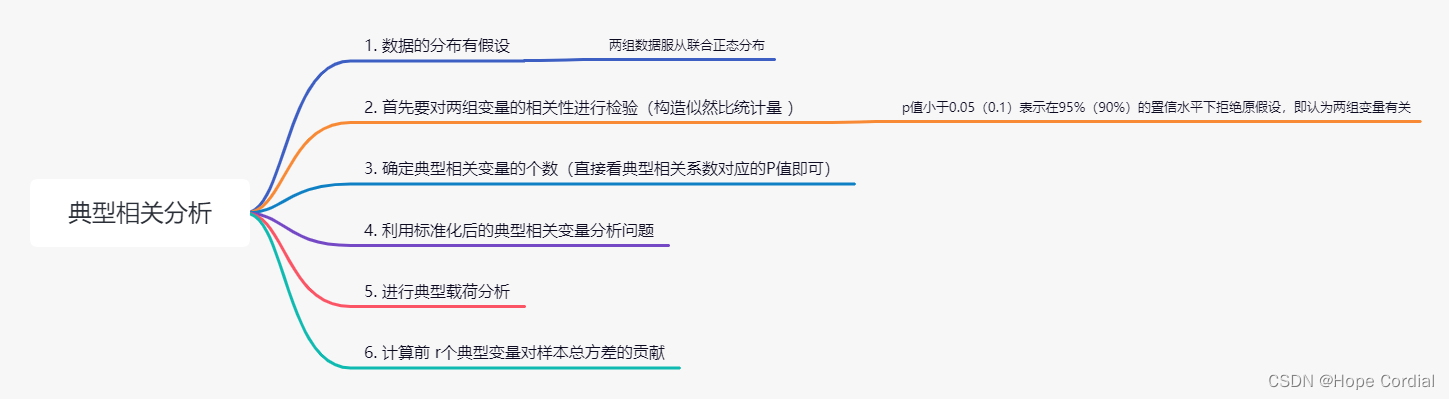

3.算法流程
- 数据的分布有假设:两组数据服从联合正态分布;
- 首先要对两组变量的相关性进行检验(构造似然比统计量 );
- 确定典型相关变量的个数(直接看典型相关系数对应的P值即可);
- 利用标准化后的典型相关变量分析问题;
- 进行典型载荷分析;
- 计算前 r 个典型变量对样本总方差的贡献。
(具体看课件PPT)
总结
暂无
最后
以上就是虚幻大米最近收集整理的关于数学建模 —— 降维算法前言一、主成分分析(PCA)二、因子分析(FA)三、典型相关性分析(CCA)总结的全部内容,更多相关数学建模内容请搜索靠谱客的其他文章。








发表评论 取消回复