二叉树的遍历及根据遍历反推树的方法详解

98 阅读 0 评论 65 点赞

我是靠谱客的博主谦让小蚂蚁，最近开发中收集的这篇文章主要介绍二叉树的遍历及根据遍历反推树的方法详解，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

一、前导-关于树的定义

森林（forest）：每个连通分量（连通块）都是树的图。按照定义，一棵树也是森林。
生成树（spanning tree）：一个连通无向图的生成子图，同时要求是树。也即在图的边集中选择 $n - 1$ 条，将所有顶点连通。
结点的深度（depth）：到根结点的路径上的边数。
树的高度（height）：所有结点的深度的最大值。
无根树的叶结点（leaf node）：度数不超过 $1$ 的结点。
有根树的叶结点（leaf node）：没有子结点的结点。

二、二叉树的遍历

对于代码解释，我们定义树结构如下：

typedef struct TreeNode
{
    int data;
    TreeNode * left;
    TreeNode * right;
}TreeNode;

1.先序遍历

先访问根，再访问子节点。

void pre_order(TreeNode * Node)//前序遍历递归算法
{
    if(Node == NULL)
        return;
    printf("%d ", Node->data);		//显示节点数据，可以更改为其他操作。在前面
    pre_order(Node->left);
    pre_order(Node->right);
}

2.中序遍历

先访问左子树，再访问根，再访问右子树。

void middle_order(TreeNode *Node)//中序遍历递归算法
{
    if(Node == NULL)
        return;
    middle_order(Node->left);
    printf("%d ", Node->data);				//在中间
    middle_order(Node->right);
}

3.后序遍历

先访问子节点，再访问根。

void post_order(TreeNode *Node)//后序遍历递归算法
{
    if(Node == NULL)
        return; 
    post_order(Node->left);
    post_order(Node->right);
    printf("%d ", Node->data);			//在最后
}

已知中序遍历和另外一个可以求第三个。

4.树上DFS

5.树上BFS(层序遍历)

三、根据遍历反推树

已知中序遍历和另外一个可以求第三个，实质上是根据两个遍历反推出整个树的结构，然后进行遍历输出。具体请看下面：

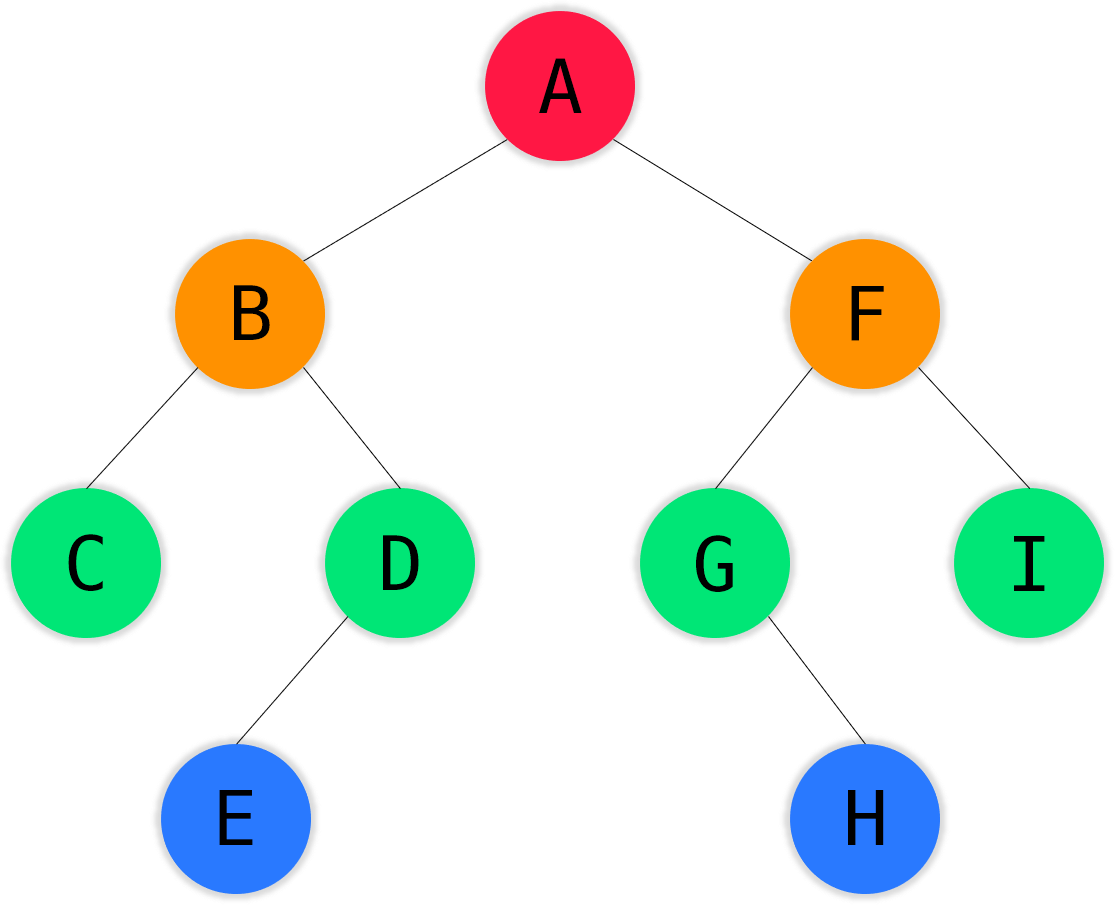
在这里插入图片描述

如图所示，该二叉树的前序遍历：ABCDEFGHI；中序遍历：CBEDAGHFI；后序遍历：CEDBHGIFA

1.根据前序遍历和中序遍历求后续遍历

下面我们模拟根据前序遍历和中序遍历构建二叉树的过程：

我们已经知道：前序遍历按照先访问根，再访问子节点的顺序进行遍历；中序遍历则按照先访问左子树，再访问根，再访问右子树的顺序进行遍历，那么我们可以确定一个恢复树结构的思路：

首先根据先序遍历开头确定根节点A：第一个节点一定是根节点
根据中序遍历的性质，从A进行分割，将整棵二叉树划分为左子树和右子树，左子树中序遍历BCDE；右子树中序遍历GHFI
根据左子树下后序遍历分割先序遍历，左子树先序遍历BCDE；右子树先序遍历FGHI
重复做前面的过程，根据先序遍历确定当前层的根节点，再分割树，直至中序遍历只剩一个节点为止停止递归

详细过程：

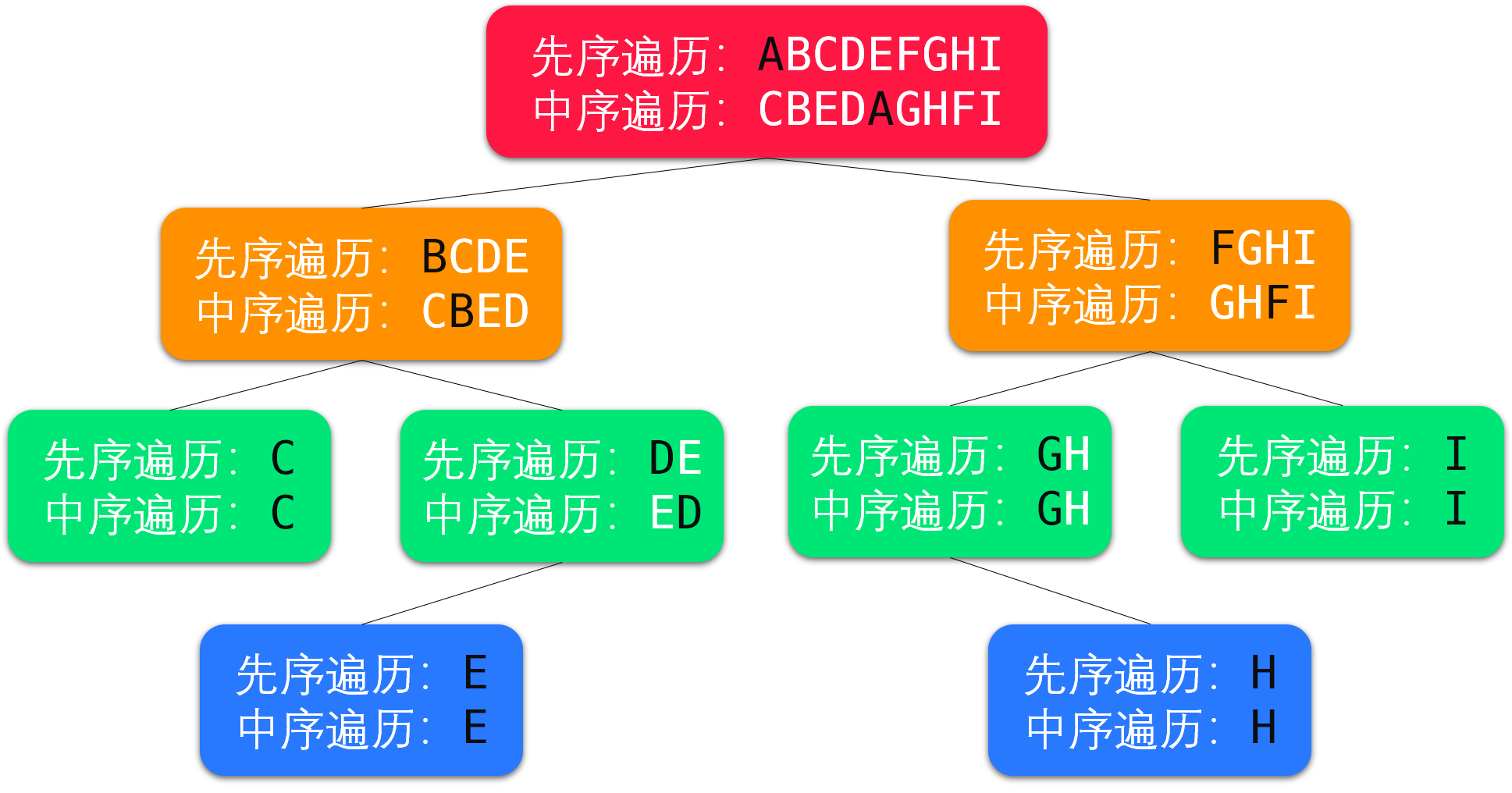
先序遍历+中序遍历

代码实现：

TreeNode *createA(char *front, char *mid, int num){
    if(num == 0) return NULL;
    char c = front[0];
    int i = 0;
    while(mid[i] != c && i < num) i++;
    int leftchild = i, rightchild = num - i - 1;
    TreeNode *root = new(TreeNode);
    root -> data = c;
    root -> left = createA(&front[1], &mid[0], leftchild);
    root -> right = createA(&front[leftchild + 1], &mid[i + 1], rightchild);
    return root;
}

2.根据后续遍历和中序遍历求前序遍历

继续使用示例图：

已知中序遍历：CBEDAGHFI；后序遍历：CEDBHGIFA

我们已经知道：中序遍历按照先访问左子树，再访问根，再访问右子树的顺序进行遍历；后序遍历按照先访问子节点再访问根节点的顺序进行遍历，那么我们可以确定一个恢复树结构的思路：

首先根据后序遍历末尾确定根节点A，最后一个点一定是根节点
在中序遍历中根据A将树分割为左子树和右子树，左子树中序遍历BEDA；右子树中序遍历GHFI
再根据左子树后序遍历CEDB；右子树后序遍历HGIF分别确定当前层的节点
重复上述过程，直至中序遍历只剩一个节点

详细过程：

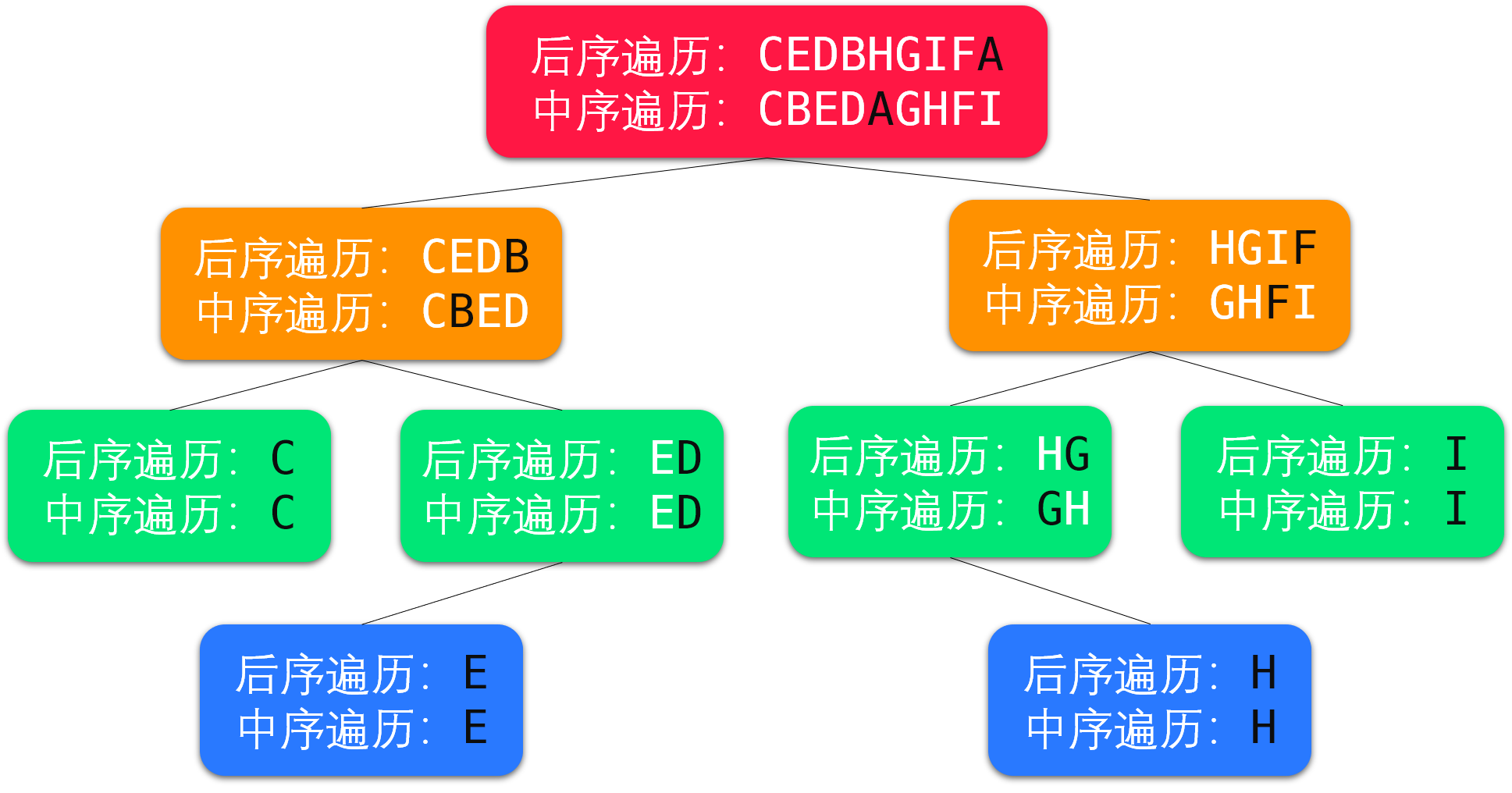
后序遍历+中序遍历

代码实现：

TreeNode *createB(char *post, char *mid, int num){
    if(num == 0) return NULL;
    char c = post[num - 1];
    int i = 0; 
    while(mid[i] != c && i < num) i++;
    int leftchild = i, rightchild = num - i - 1;
    TreeNode *root = new(TreeNode);
    root -> data = c;
    root -> left = createB(&post[0], &mid[0], leftchild);
    root -> right = createB(&post[leftchild], &mid[i + 1], rightchild);
    return root;
}