[LCT 刷题][树链信息维护] P2486 [SDOI2011]染色

57 阅读 0 评论 38 点赞

我是靠谱客的博主聪明菠萝，最近开发中收集的这篇文章主要介绍[LCT 刷题][树链信息维护] P2486 [SDOI2011]染色，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目思路

题目要求维护树上序列不同颜色段数，涉及到树链的性质，因此考虑用LCT解决。

但是我们可以发现：颜色段计数跟线段树有点不一样。我们需要对树链上的每条边进行转换，将两个端点共色的边设为 $0$ ，异色的设为 $1$ ，那么最终答案就变成了树链上的和。

但是我们发现这个题涉及了动态修改，因此我们需要单独的维护每条边，即在LCT的Splay节点上维护每个节点 $x$ 自身的颜色 $x c$ ，其左儿子的颜色 $l c$ ，其右儿子的颜色 $rc$ ，然后考虑如何上传答案：

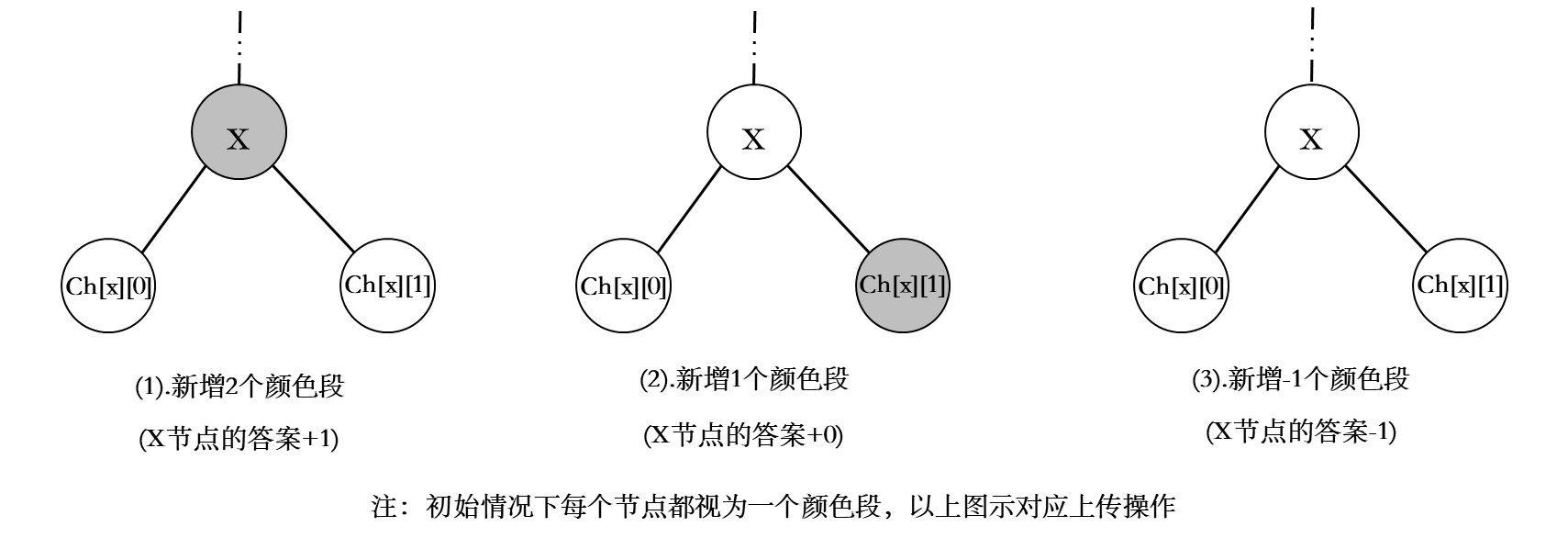
我们将上传分为三种情况讨论：
在这里插入图片描述

当前节点 $x$ 与其左右儿子都异色，由于Splay节点 $x$ 左儿子在原树的深度一定小于 $x$ ， $x$ 右儿子深度大于 $x$ ，即 $x$ 一定充当了分割点的作用，因此新增了2个颜色段。如果初始每个点都视为一个颜色段，那么就是新增了1个颜色段；
当前节点 $x$ 与其左儿子或右儿子异色，此时共色节点构成同一颜色段，异色节点构成新段，因此新增1个颜色段；如果初始每个点都视为一个颜色段，那么就是新增了0个颜色段；
当前节点 $x$ 与其左右儿子都同色，显然三个点在原树上共属一个颜色段，那么新增0个颜色段，如果初始每个点都视为一个颜色段，那么就是新增了-1个颜色段；

需要注意的是，在push_up前需要保证当前节点的懒标记已经 $push_down$ 完毕。

Code

#include <bits/stdc++.h>
#pragma gcc optimize("O2")
#pragma g++ optimize("O2")
#define int long long
#define endl 'n'
using namespace std;

const int N = 2e5 + 10, MOD = 1e9 + 7;

namespace LCT{
    struct Info{
        int ans, lc, rc, xc, ctag;
        void init_color(int c) { lc = rc = xc = c, ans = 1; }
    }tree[N];
    int ch[N][2], f[N], tag[N];
    #define ls ch[x][0]
    #define rs ch[x][1]

    inline void push_reverse(int x) { swap(ls, rs), swap(tree[x].lc, tree[x].rc), tag[x] ^= 1; }

    inline void push_color(int x, int c) { tree[x].init_color(c); tree[x].ctag = c; }

    inline void push_down(int x) {
        if(tree[x].ctag) {
            push_color(ls, tree[x].ctag);
            push_color(rs, tree[x].ctag);
            tree[x].ctag = 0;
        }
        if(tag[x]) {
            if(ls) push_reverse(ls);
            if(rs) push_reverse(rs);
            tag[x] = 0;
        }
    }

    inline void push_up(int x) {
        push_down(ls), push_down(rs);
        tree[x].lc = ls ? tree[ls].lc : tree[x].xc;
        tree[x].rc = rs ? tree[rs].rc : tree[x].xc;
        if(ls && rs) tree[x].ans = tree[ls].ans + tree[rs].ans + 1 - (tree[ls].rc == tree[x].xc) - (tree[rs].lc == tree[x].xc);
        else if(ls) tree[x].ans = tree[ls].ans + (tree[ls].rc != tree[x].xc);
        else if(rs) tree[x].ans = tree[rs].ans + (tree[rs].lc != tree[x].xc);
        else tree[x].ans = 1;
    }

    #define get(x) (ch[f[x]][1] == x)                        
    #define isRoot(x) (ch[f[x]][0] != x && ch[f[x]][1] != x)

    void rotate(int x) {
        int y = f[x], z = f[y], k = get(x);
        if(!isRoot(y)) ch[z][ch[z][1] == y] = x;
        ch[y][k] = ch[x][!k], f[ch[x][!k]] = y;
        ch[x][!k] = y, f[y] = x, f[x] = z;
        push_up(y); push_up(x);
    }

    void update(int x) {
        if(!isRoot(x)) update(f[x]);
        push_down(x);
    }

    void splay(int x) {
        update(x);
        for(int fa = f[x]; !isRoot(x); rotate(x), fa = f[x]) {
            if(!isRoot(fa)) rotate(get(fa) == get(x) ? fa : x);
        }
        push_up(x);
    }

    int access(int x) {
        int p;
        for(p = 0; x; x = f[p = x]) splay(x), rs = p, push_up(x);
        return p;
    }

    void makeRoot(int x) { access(x), splay(x), push_reverse(x); }

    int findRoot(int x) {
        access(x), splay(x);
        while(ch[x][0]) push_down(x), x = ch[x][0];
        splay(x);
        return x;
    }

    void split(int x, int y) {
        makeRoot(x);
        access(y), splay(y);
    }

    void link(int x, int y) {
        makeRoot(x);
        if(findRoot(y) != x) f[x] = y;
    }

    void cut(int x, int y) {
        makeRoot(x);
        if(findRoot(y) == x && f[y] == x && !ch[y][0]) {
            f[y] = ch[x][1] = 0;
            push_up(x);
        }
    }
}

inline void solve(){
    int n, m; cin >> n >> m;
    for(int i = 1, c = 0; i <= n; i++) cin >> c, LCT::tree[i].init_color(c);
    for(int i = 1; i < n; i++) {
        int u, v; cin >> u >> v;
        LCT::link(u, v);
    }

    while(m--) {
        char op; cin >> op;
        if(op == 'C') {
            int u, v, c; cin >> u >> v >> c;
            LCT::split(u, v); 
            LCT::push_color(v, c);
        } else if(op == 'Q') {
            int u, v; cin >> u >> v;
            LCT::split(u, v);
            cout << LCT::tree[v].ans << endl;
        }
    }

}

signed main(){
    ios_base::sync_with_stdio(false), cin.tie(0);
    cout << fixed << setprecision(12);
    int t = 1; // cin >> t;
    while(t--) solve();
    return 0;
}