可持久化线段树 主席树 详解

一、可持久化线段树 简介

可持久化线段树，顾名思义，即对线段树进行可持久化处理之后的线段树。

在可持久化数据结构的理论中，我们对可持久化的概念有所了解：“可以返回之前的某个状态，并在该基础上进行修改”。可持久化线段树就是这样一种结构。

我们从一般思路出发进行分析：想要让线段树可持久化，最朴素的方法就是每进行一次操作都新建一颗线段树。但显然这是不明智的做法：时间和空间上而言都是非常差的的算法。我们不妨继续分析一下更新之后与更新之前的结构：每次更新都只有少量的点被修改。因此大量的点可以继续使用，无需重新建树。

本文分两个部分对可持久化线段树进行探讨。

值得注意的是：我们一般认为主席树就是可持久化线段树，实际上两者之间有区分：

可持久化线段树单纯指经过可持久化处理之后，能够查询、修改历史节点数据的结构，建立在基础线段树的基础之上；而主席树建立在权值线段树的基础之上，能够查询修改历史节点。二者本质区别在于纪念性可持久化的对象所维护的对象不同(一个维护权值、一个维护值域)。

因此，可持久化线段树$\ne$主席树，准确的说，主席树$\subset$可持久化线段树。

二、可持久化线段树 基本结构与操作

1.基本结构、建树操作

首先应该明确一点：由于可持久化结构重叠的特殊性，可持久化线段树不能采用堆式储存，因此只能采取动态开点的方式进行储存。

不同于后续节点的更新，对于最初的状态下的线段树我们采用一次建树完成：

1. 采用递归建树，递归函数参数保存左右边界(初始化为$(1,n)$)、当前元素的指针。同时保存总计数$cnt$；

2. 递归边界控制为$l==r$，由于此时左边界$l$即为指向$a$数组的指针，因此叶子节点赋值$val(p)=a[l]$ ；

3. 非叶子节点首先记录左右子节点的下标$ls(p)=cnt++,rs(p)=cnt++$，然后递归建左右子树：

   $build(l,mid,ls(p))、build(mid+1,r,rs(p))$

4. 建立左右节点后非叶子节点 = 左右子节点的和：$val(p)=val(ls(p))+val(rs(p))$

根据以上建树过程，我们以数组$a=1,2,3,4,5$为例建立线段树：

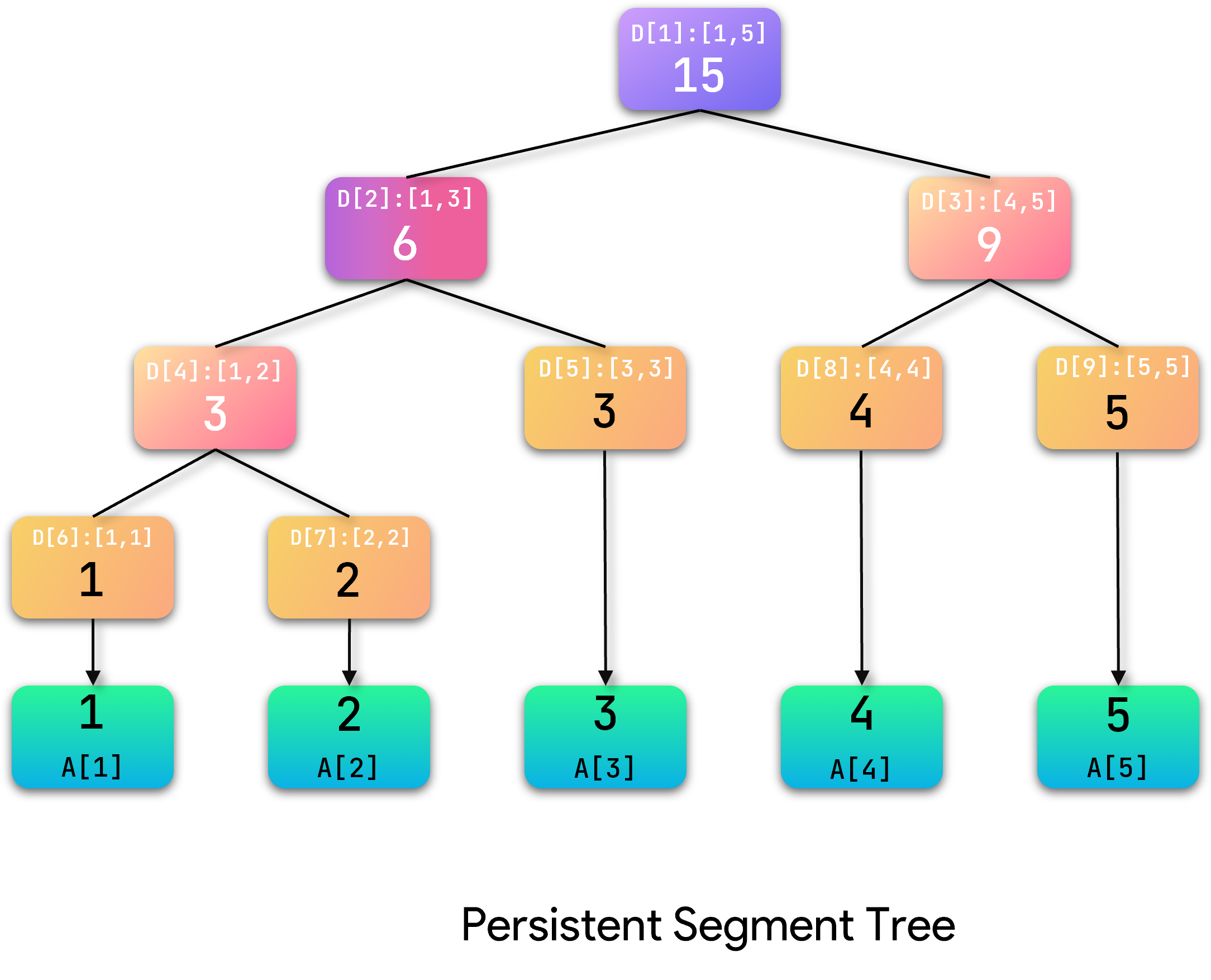
可以看到：不同于基础线段树，可持久化线段树的下标不再遵循堆的规律，这种建树方式我们称为动态开点。

结构体封装版：

#define ls(x) tree[x].ls
#define rs(s) tree[x].rs
#define val(x) tree[x].val
#define mark(x) tree[x].mark
struct node{
    int val, mark = INT_MIN;
    int ls, rs;
}tree[MAXN];

void build(int l = 1, int r = n, int p = 1){
    if(l == r) val(p) = a[l];
    else{
        ls(p) = ++cnt, rs(p) = ++cnt;
        int mid = (l + r) >> 1;
        build(l, mid, ls(p));
        build(mid + 1, r, rs(p));
        val(p) = val(ls(p)) + val(rs(p));
    }
}

建树完毕后，上述线段树已经静态化，后续的修改操作通过增加新节点来实现。

2.单点修改

假设现在要对$A[4]$加$-2$，则操作步骤如下：

首先建立新根结点，更新根节点记录数组：$root[flag]=++cnt$

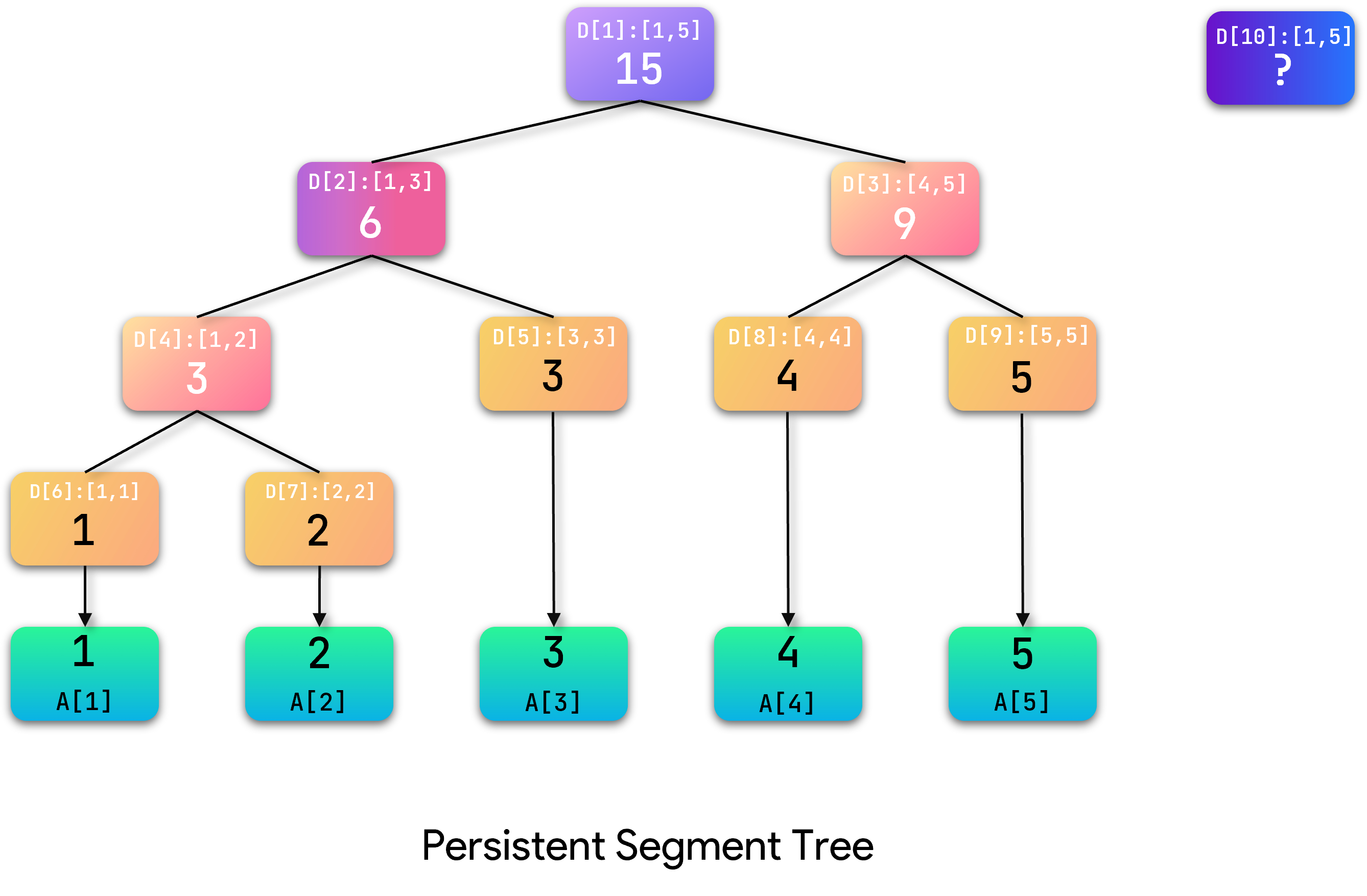
创建新节点后对其进行处理。由于我们要修改的元素$A[4]$位于右子树，因此左子树部分保持不变，可以继续使用。因此将原左子树与新节点相连，同时新建右子节点。

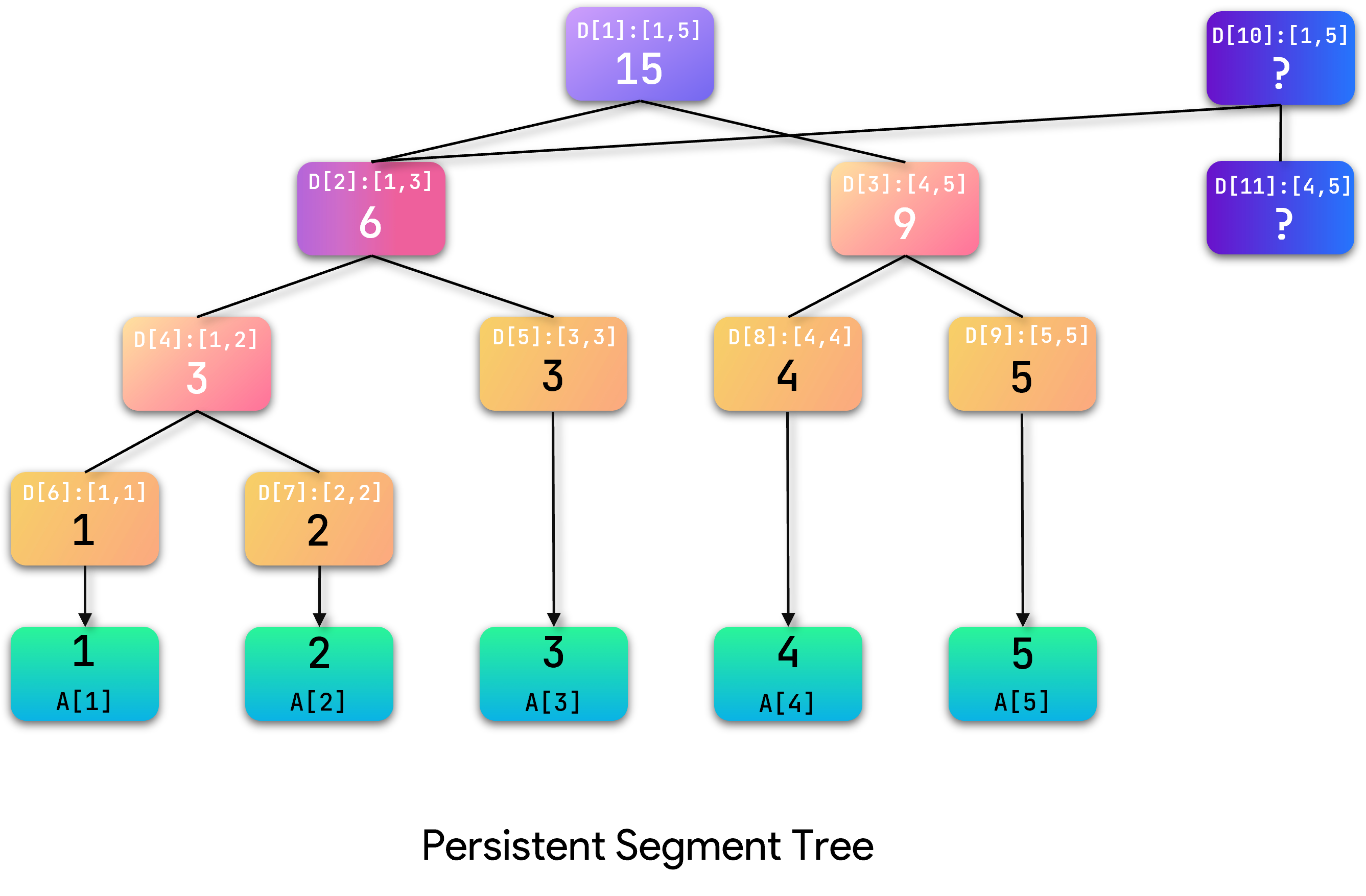
继续处理，$A[4]$位于当前结点左子树，右子树保持不变继续使用，因此新建左子节点，将原右子节点与新节点相连。

继续访问左子节点发现到达叶子结点，对原数据进行处理后再逐层回溯，更新路径上的结点值。

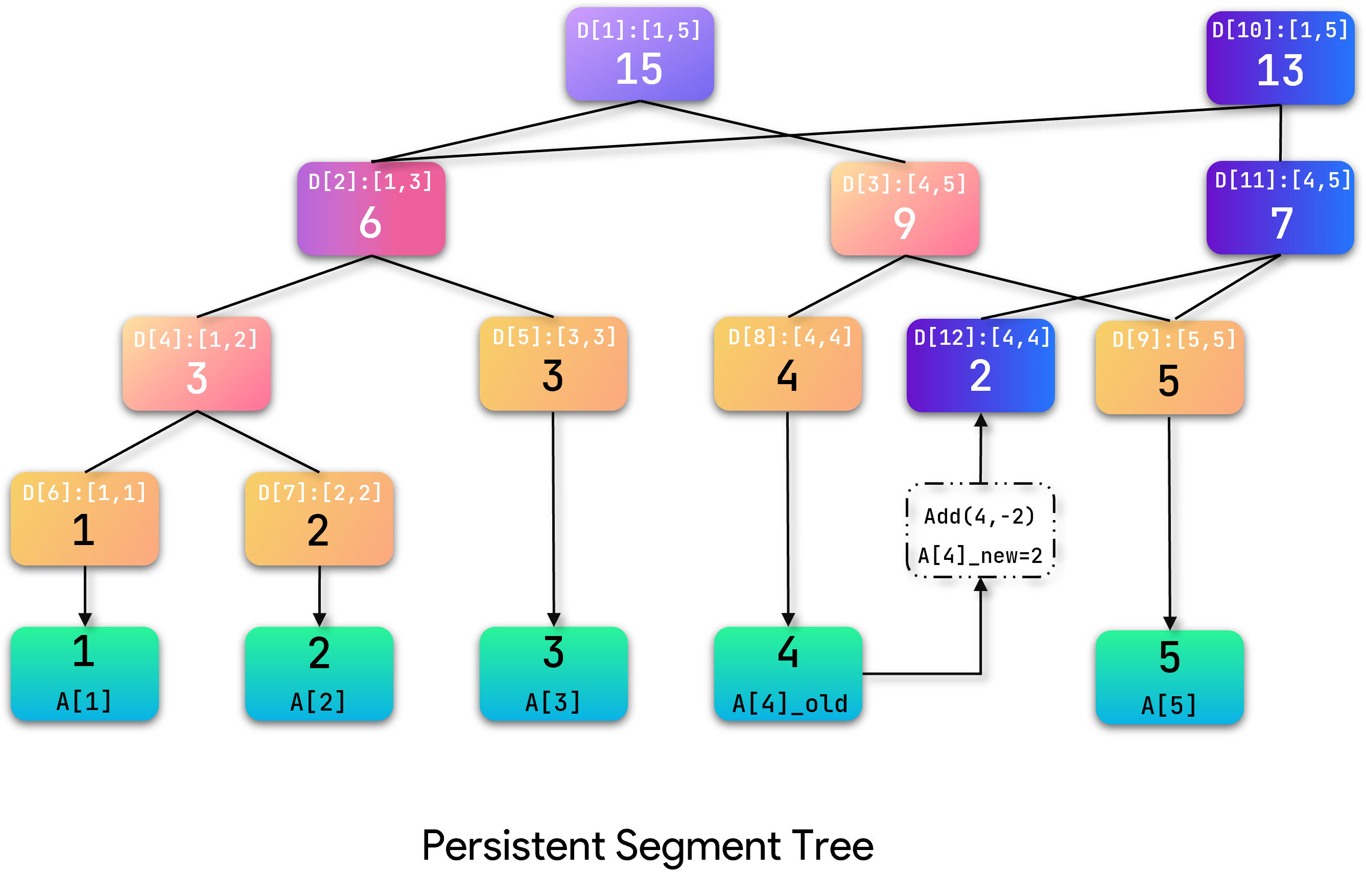
单点修改的操作到此结束。可以看到，对于最初版本的线段树，其任何数据未被改变。

void update(int x, int d, int p, int q, int cl = 1, int cr = n){
    if (cl == cr) val(q) = val(p) + d; // 给叶子节点赋值
    else{
        ls(q) = ls(p), rs(q) = rs(p); // 复制节点
        int mid = (cl + cr) / 2;
        if (x <= mid) ls(q) = ++cnt, update(x, d, ls(p), ls(q), cl, mid); 
        // 创建新节点作为左儿子，然后往左递归
        else rs(q) = ++cnt, update(x, d, rs(p), rs(q), mid + 1, cr); 
        // 创建新节点作为右儿子，然后往右递归
        val(q) = val(ls(q)) + val(rs(q)); // 根据子节点给当前节点赋值
    }
}

3.区间查询

区间查询与基础线段树几乎一致，只需要额外关注查询的版本对应的根节点即可。

int query(int l, int r, int p, int cl = 1, int cr = n){
    if (cl > r || cr < l) return 0;
    else if (cl >= l && cr <= r) return val(p);
    else{
        int mid = (cl + cr) / 2;
        return query(l, r, ls(p), cl, mid) + query(l, r, rs(p), mid + 1, cr);
    }
}

4.区间修改

我们需要再次回到$Lazy$标记上进行讨论：

对于$Lazy$标记，我们其实有两种实现方案：

1. 标记上下传，也就是我们最常用的$puush\_up、push\_down$操作；
2. 标记永久化：标记时不用$puush\_up、push\_down$，而是在查询的时候干预数据。

二者的一大区别在于，标记上下传会引发修改结点路径上的点的更新，而标记永久化不会影响树上的点。

这点区别是非常有意义的：考虑一棵可持久化线段树，如果从某节点上传，则到根节点路径上的点都会被修改，而可持久化结构导致了某些结点的复用，这会引发多个版本的线段树更新，无法指定是哪一版本；同理，下传标记也会引发不必要的点的更新。因此，我们只能通过标记永久化对可持久化线段树进行修改。

于是，我们在查询时需要额外带上一个标记：$mk$

我们不妨再回顾一下查询的过程：

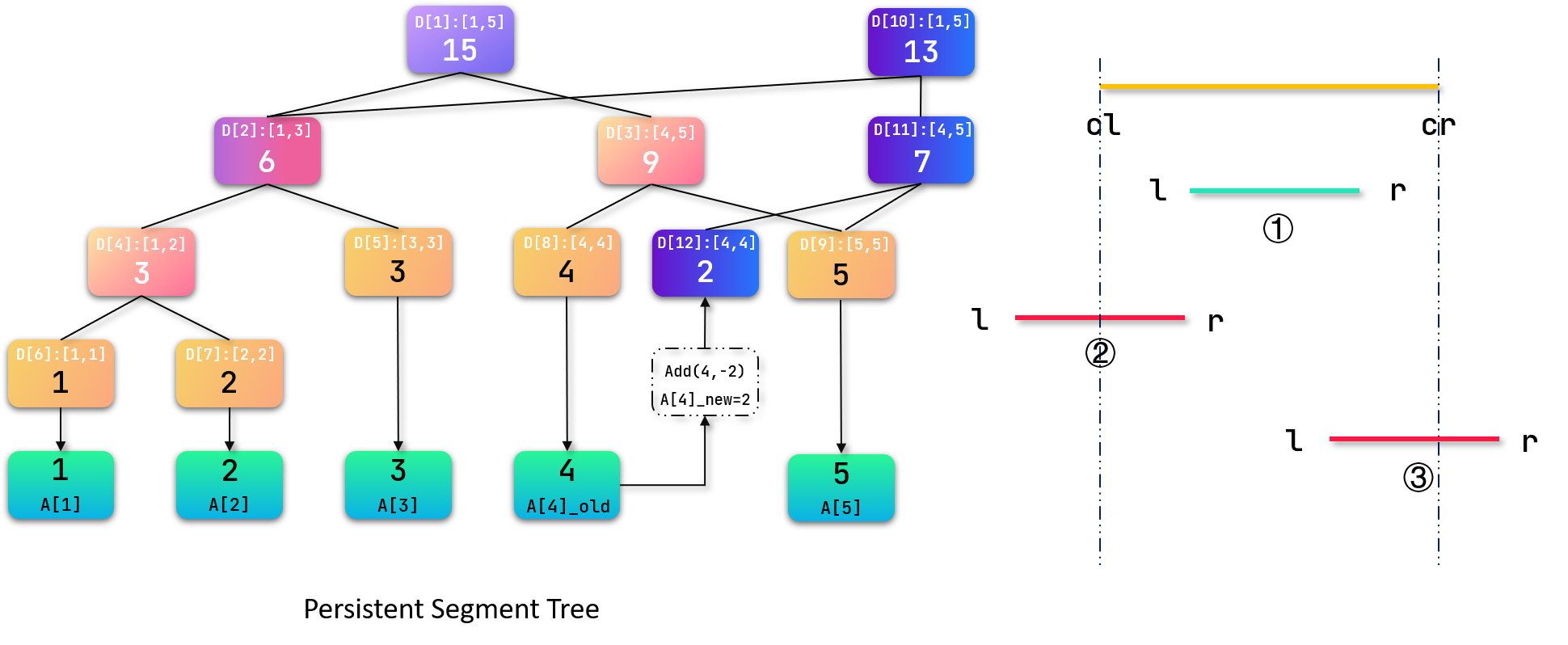
我们曾在线段树的查询过程中了解到：查询的过程就是不断地查询区间的交集，以此不断地缩小查找范围。

如上图所示，假设查询到①所示的区间则返回该节点的值，因为他是待查询区间的子集；②所示的区间则需要向右递归搜索、③向左递归搜索。

不同于基础线段树，可持久化线段树需要进行额外加永久化标记的操作，即：查询到待查区间的子集时，返回(该节点值$+$子集元素个数$\times$永久化标记)

同时，递归查询时也要额外对标记进行累加。这点也十分容易理解：

我们思考永久标记的意义：对于当前节点所管辖的区间元素全部加某个值(或者做出某种改变)，因此向下查询子集时应该带上当前节点的标记，相当于将标记进行了下放。

ll query(int l, int r, int p, int cl = 1, int cr = n, ll mk = 0){
    if (cl > r || cr < l) return 0;
    else if (cl >= l && cr <= r) return val(p) + mk * (cr - cl + 1); // 加上带的标记
    else{
        int mid = (cl + cr) >> 1;
        return query(l, r, ls(p), cl, mid, mk + mark(p)) + query(l, r, rs(p), mid + 1, cr, mk + mark(p)); // 带着标记传递
    }
}

对于$update$操作，其基本过程如下：

1. 首先对当前节点进行复制；
2. 判断：如果当前节点管辖区间合法，且是待修改区间的子集，那么对当前新的节点(复制后的节点)的标记执行加操作；
3. 如果不满足$2$条件，则判断待修改区间是否由左子树管辖、是否由右子树管辖，如果是则复制节点，递归向左右建点更新。

值得注意的是，由于缺少传递标记，因此由子节点给当前节点赋值可能会发生错误。

为了得到全包含的区间并计算真实长度，我们只需要定义区间为$[max(l,cl),min(r,cr)]$即可(保证其为带查询区间的子集)。

void update(int l, int r, int d, int p, int q, int cl = 1, int cr = n){
    ls(q) = ls(p), rs(q) = rs(p), mark(q) = mark(p); // 复制节点
    if (cl >= l && cr <= r && cr > cl) mark(q) += d;
    else{
        int mid = (cl + cr) >> 1;
        if (cl <= r && mid >= l) ls(q) = ++cnt, update(l, r, d, ls(p), ls(q), cl, mid);// 提前进行判断，以免新建不必要的节点
        if (mid + 1 <= r && cr >= l) rs(q) = ++cnt, update(l, r, d, rs(p), rs(q), mid + 1, cr);
            
    }
    val(q) = val(p) + (min(cr, r) - max(cl, l) + 1) * d; // 根据需要更新的区间长度计算当前节点的值
}

三、主席树

区别于一般的可持久化线段树，主席树是可持久化权值线段树。

下面简单介绍一下主席树的构造过程：

1.建立空树

void build(int l = 1, int r = n, int p = 1){
    val(p) = 0;
    if (l != r){
        ls(p) = ++cnt, rs(p) = ++cnt;
        int mid = (l + r) / 2;
        build(l, mid, ls(p));
        build(mid + 1, r, rs(p));
    }
}

2.区间离散化

int C[MAXN], L[MAXN], ori[MAXN];
void discretize(int A[], int n){
    memcpy(C, A, sizeof(int) * n);     // 复制
    sort(C, C + n);                    // 排序
    int l = unique(C, C + n) - C;      // 去重
    for (int i = 0; i < n; ++i){
        L[i] = lower_bound(C, C + l, A[i]) - C + 1; // 查找
        ori[L[i]] = A[i]; // 保存离散化后的数对应的原数
    }

3.插入离散化数据

for (int i = 0; i < n; i++){
    roots[i + 1] = ++cnt;
    update(L[i], 1, roots[i], roots[i + 1]);
}

4.查询区间第$K$大/小

我们已经有了求[1, r]内第k大数的方法（查询相应历史版本即可），而求[l, r]内第k小数，只需对kth函数稍作修改。注意，我们在求kth时会用到当前左儿子对应的区间和，现在要排除[1, l-1]，那么把这部分和减去即可。

这一部分的思想与权值树状数组很相似。

int kth(int k, int p, int q, int cl = 1, int cr = n){
    if (cl == cr) return ori[cl];
    int mid = (cl + cr) / 2;
    if (val(ls(q)) - val(ls(p)) >= k) return kth(k, ls(p), ls(q), cl, mid); // 往左搜
    else return kth(k - (val(ls(q)) - val(ls(p))), rs(p), rs(q), mid + 1, cr); // 往右搜
}

时间复杂度$O(\log n)$。

本文部分内容参考自算法学习笔记(50): 可持久化线段树 - 知乎 (zhihu.com)

最后

以上就是聪慧日记本为你收集整理的可持久化线段树 主席树 详解的全部内容，希望文章能够帮你解决可持久化线段树 主席树 详解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。