几何分布

几何分布是伯努利分布的推广，不断重复伯努利试验，直到首次成功为止，随机变量$X$表示首次成功时已经完成的试验次数，我们称 $X$ 是一个服从几何分布的随机变量

适用情况举例

实际中有不少随机变量服从几何分布，譬如，某产品的不合格率为0.05，则首次查到不合格品的检查次数 $X～\text{Geom}(0.05)$ 【引用自：几何分布】

截图来源：Geometric distribution

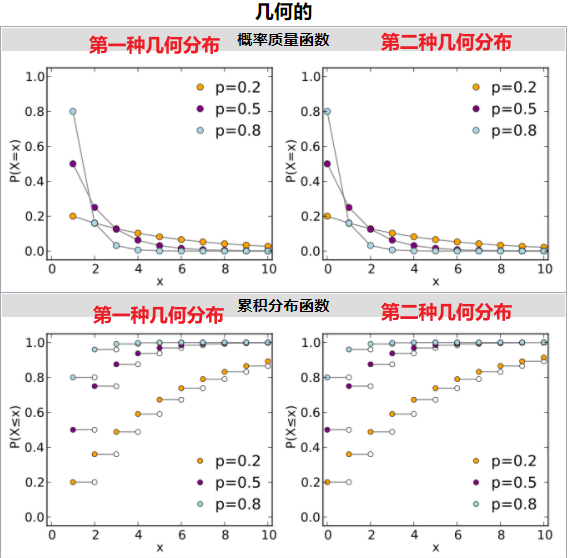
截图来源：几何分布

第一种情况对应上面第一种几何分布、第二种情况对应上面第二种几何分布

截图来源：Geometric distribution

我们这里介绍的是第一种几何分布

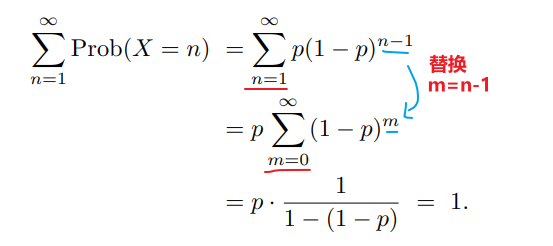
均值和方差
我们用 ${\mu }_X$ 表示均值
第一轮试验：第一次试验成功，成功概率为 $p$，已经完成的试验次数 $X=1$，此轮试验的期望 $1\cdot p$
第二轮试验：第一次试验失败，已经完成试验次数 $X=1$，期望为 $1\cdot (1-p)$，试验重新开始，前 $E[X]$ 次试验失败，失败概率 $1-p$，已经完成的试验次数 $X=E[X]$，期望约为 $E[X](1-p)$，
第二轮试验的期望 $1\cdot (1-p)+E[X](1-p)=(E[X]+1)(1-p)=E[1+X](1-p)$，
其中$E[1+X]$代表第一次试验失败，试验重新开始后，试验$E[X]$次失败

$$\begin{gathered} E[X]=1\cdot p+E[X+1](1-p) \\ pE[X]=1 \\ {\mu }_X=E[X]=\frac{1}{p} \end{gathered}$$

$$\begin{gathered} E[X^2]=1\cdot p+E[(1+X{)}^2](1-p) \\ E[X^2]=p+(1+2E[X]+E[X^2])(1-p) \\ E[X^2]=\frac{1+2(1-p)E[X]}{p} \\ \text{Var}=E[X^2]-E[X{]}^2=\frac{1-p}{p^2} \end{gathered}$$

例子：

截图来源：Geometric distribution

最后

以上就是烂漫鞋子为你收集整理的几何分布（一种离散分布）几何分布的全部内容，希望文章能够帮你解决几何分布（一种离散分布）几何分布所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。