直方图均衡化
简介
直方图是图像中像素强度分布的图形表达方式。它统计了每一个强度值所具有的像素个数。直方图均衡化是通过拉伸像素强度分布范围来增强图像对比度的一种方法。是图像处理领域中利用图像直方图对对比度进行调整的方法。均衡化指的是把一个分布(给定的直方图)映射到另一个分布(一个更宽更统一的强度值分布),所以强度值分布会在整个范围内展开。映射函数应该是一个累积分布函数。直方图均衡化是通过调整图像的灰阶分布,使得在0~255灰阶上的分布更加均衡,提高了图像的对比度,达到改善图像主观视觉效果的目的。对比度较低的图像适合使用直方图均衡化方法来增强图像细节。这种方法通常用来增加许多图像的全局对比度,尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法,亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度,直方图均衡化通过有效地扩展常用的亮度来实现这种功能。这种方法对于背景和前景都太亮或者太暗的图像非常有用,这种方法尤其是可以带来X光图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。这种方法的一个主要优势是它是一个相当直观的技术并且是可逆操作,如果已知均衡化函数,那么就可以恢复原始的直方图,并且计算量也不大。这种方法的一个缺点是它对处理的数据不加选择,它可能会增加背景噪声的对比度并且降低有用信号的对比度。
彩色图像直方图均衡化:上面描述了灰度图像上使用直方图均衡化的方法,但是通过将这种方法分别用于图像RGB颜色值的红色、绿色和蓝色分量,从而也可以对彩色图像进行处理。
数学原理
图像直方图的定义
定义1:一个灰度级在范围[0,L-1]的数字图像,其直方图是一个离散函数
其中n是图像的像素总数,是图像中第k个灰度级的像素总数,
是第k个灰度级,
定义2:一个灰度级别在范围[0,L-1]的数字图像的直方图是一个离散函数
由于的增量是1,直方图可表示为:
,即。图像中不同灰度级像素出现的次数。
这两种图像直方图定义使函数值正则化到[0,1]区间,成为实数函数,并且函数值的范围与像素的总数无关,定义给出了灰度级在图像中出现的概率密度统计。
直方图变换的理论基础
对于连续函数而言,假设其变换函数为:
在原始图像中,对于每一个像素值r产生一个灰度值s。其中,变换函数要满足以下条件:
(1)在区间
中为单值且单调递增。这是为了保证其逆函数的存在,并且输出图像从黑到白顺序增加;
(2)当,
。这保证输出灰度级与输入有同样的范围。把上函数的逆函数表示为
一幅图像的灰度级可被视为区间[0,1]的随机变量。随机变量的一个最重要的基本描述是其概率密度函数。令和
分别代表随机变量r和s的概率密度函数。此处带有下标的
和
用于表示不同的函数。由基本概率理论得到的一个基本结果:如果
和
已知,且
满足公式1,那么变换变量s的概率密度函数
可由以下简单公式得到:
因此,变换变量$s$的概率密度函数由输入图像的灰度级概率密度函数和所选择的变换函数所决定。
在图像处理中一个尤为重要的变换函数:
该被积函数其值为正,并且函数积分是一个函数曲线下的面积,其内含为随机变量r的累积分布函数,所以它遵守该变换函数是单值单调增加的条件,因此满足条件(1)。同样地,区间[0,1]也满足条件(2)。其积分过程如下:
用这个结果代替,待入式4,取概率为正,得到:
因为是概率密度函数,在这里可以得到区间[0,1]以外它的值为0,可见式6中给出的
形式为均匀概率密度函数。换句话来说,公式4给出的变换函数会得到一个随机变量,其特征为一个均匀概率密度函数,与
的函数形式是无关的。总述以上,可以看出
就是一个直方图均衡化的基本原理,该等式右边的意义就是随机变量r的累积分布函数。这样便转化成了求输入图像灰度级r的累积分布函数。
下面开始讨论离散函数。对于离散值,处理的是它函数概率的和,而不是概率密度函数的积分。一幅图像中灰度级$r_k$出现的概率近似为:
其中,n是图像中像素的总和,是灰度级为
的像素个数,
为图像中可能的灰度级总数。公式4中变换函数的离散形式为:
因此,已处理的图像(即输出图像)由通过公式8,将输入图像中灰度级为的各像素映射到输出图像中灰度级为
的对应像素得到。与连续形式不同,一般不能证明离散变换能产生均匀概率密度函数的离散值(为均匀直方图)。但是不论怎么样,可以很容易地看出式8的应用有展开输入图像直方图的一般趋势,以至于直方图均衡化过的图像灰度级能跨越更大的范围。至此,便给出了整个的证明过程。
直方图均衡化步骤
下面给出了直方图均衡化的一般实现过程:
(1)统计原始输入图像各灰度级的像素数目,其中
为灰度总级数;
(2)计算原始图像直方图,即各灰度级的概率密度,,
为原始图像的总像素数目;
(3)计算累积分布函数:
(4)计算最后的输出灰度级,
代码及结果展示
function Histogramequalization()
[f,p]=uigetfile('*.*','选择图像文件');
if f
I=imread(strcat(p,f));
end
h=figure();
set(h,'position',[300 100 1000 600]);
Ir=I(:,:,1);%提取红色分量
Ig=I(:,:,2);%提取绿色分量
Ib=I(:,:,3);%提取蓝色分量
I1=histogram(Ir); %直方图均衡化函数histeq
I2=histogram(Ig);
I3=histogram(Ib);
c=cat(3,I1,I2,I3); %cat用于构造多维数组
subplot(2,4,1);imshow(I);
title('A). 原始图像');
subplot(2,4,5);imshow(c);
title('B). 直方图均衡化');
subplot(2,4,2);
imhist(Ir);
title('I). 红色分量直方图');
subplot(2,4,6);
imhist(I1);
title('II). R均衡化后直方图');
subplot(2,4,3);
imhist(Ig);
title('I). 绿色分量直方图');
subplot(2,4,7);
imhist(I2);
title('II). G均衡化后直方图');
subplot(2,4,4);
imhist(Ib);
title('I). 蓝色分量直方图');
subplot(2,4,8);
imhist(I3);
title('II). B均衡化后直方图');
%调用的(直方图均衡化)构造函数
function d=histogram(I)%构造histogram函数
J=I;
[m,n]=size(I); %确定矩阵大小
area=m*n;
a=zeros(1,256); %产生1*256的零矩阵a,用来存放原始图像各个灰度值的个数
b=zeros(1,256);
for i=1:m %记录各个灰度值的个数
for j=1:n
d=I(i,j)+1; %获取(i,j)位置的灰度值(注意:灰度值为0-255,对应矩阵的1-256)
a(1,d)=a(1,d)+1; %矩阵a上对应灰度值的计数+1
end
end
for i=1:256 %均衡化
sum=0;
for j=1:i
sum=sum+a(1,j);
end
b(1,i)=sum*255/area;
end
for i=1:m %用均衡化后的数据代替原位置的数据
for j=1:n
d=J(i,j)+1;
J(i,j)=b(1,d);
end
end
d=J;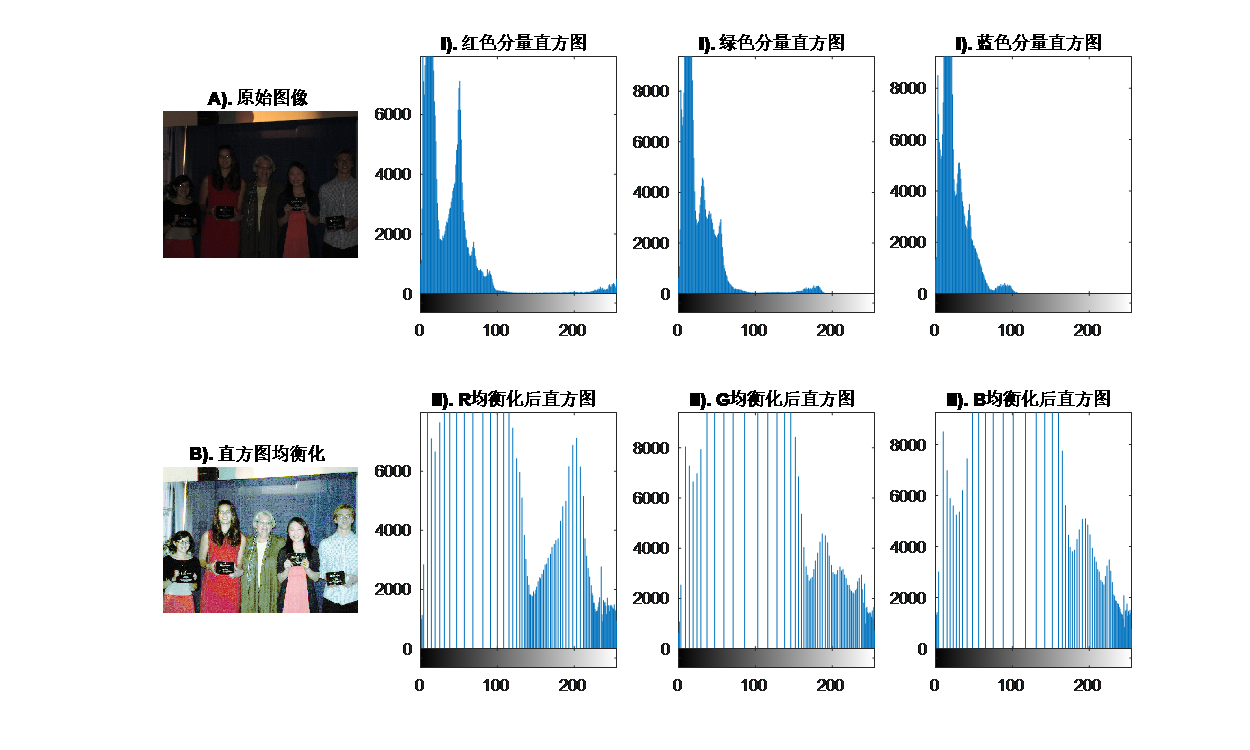
由上图可以看出,直方图均衡化将图像像素值重新分配,使一定灰度范围内的像素数量大致相同。直方图均衡化把给定图像的直方图分布改编成“均匀分布”直方图。对于背景和前景太亮或者太暗的图像非常有用,由图中可以看到直方图均衡化后,对于曝光不足或者曝光太多的照片都可以展示更多的细节。
但是缺点是:变换后图像的灰度级减少,某些细节消失;某些图像经管处理后对比度不自然地过分增强。
最后
以上就是失眠小霸王最近收集整理的关于彩色图直方图均衡化matlab直方图均衡化的全部内容,更多相关彩色图直方图均衡化matlab直方图均衡化内容请搜索靠谱客的其他文章。






![数字图像处理实践[3]---夜间图像增强](https://www.shuijiaxian.com/files_image/reation/bcimg7.png)

发表评论 取消回复