random.multivariate_normal和norm.rvs

np.random.multivariate_normal方法用于根据实际情况生成一个多元正态分布矩阵，其在Python3中的定义如下：

def multivariate_normal(mean, cov, size=None, check_valid=None, tol=None) 

其中mean和cov为必要的传参而size，check_valid以及tol为可选参数。

    mean：mean是多维分布的均值维度为1；

    cov：协方差矩阵，注意：协方差矩阵必须是对称的且需为半正定矩阵；

    size：指定生成的正态分布矩阵的维度（例：若size=(1, 1, 2)，则输出的矩阵的shape即形状为 1X1X2XN（N为mean的长度））。

    check_valid：这个参数用于决定当cov即协方差矩阵不是半正定矩阵时程序的处理方式，它一共有三个值：warn，raise以及ignore。当使用warn作为传入的参数时，如果cov不是半正定的程序会输出警告但仍旧会得到结果；当使用raise作为传入的参数时，如果cov不是半正定的程序会报错且不会计算出结果；当使用ignore时忽略这个问题即无论cov是否为半正定的都会计算出结果。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 生成2个正态分布，第1个正态分布的均值mean为116.50，方差为sigma，也就是生成的数在以mean为中心，标准差为pow(sigma,1/2)附近分散分布
#第2个正态分布的均值mean为40.41，方差为sigma
#如果是2个正态分布，其实就是生成以点位中心，以标准差为半径的圆
sigma = 0.0015  #不理解
num = 1000  # 生成样本数
# 随机生成二维正态分布样本
mean = np.array([116.50, 40.41])
cov = np.array([[sigma, 0], [0, sigma]])
sample_ary = np.random.multivariate_normal(mean, cov, num)

sample_ary_data=pd.DataFrame(sample_ary,columns=['lon','lat']) 
print(sample_ary_data)

lon_mean=sample_ary_data['lon'].mean()
print("lon均值为",lon_mean)
print("lon协方差为",sum([(i-lon_mean)*(i-lon_mean) for i in sample_ary_data['lon'].values])/(len(sample_ary_data)-1))

lat_mean=sample_ary_data['lat'].mean()
print("lat均值为",lat_mean)
print("lat协方差为",sum([(i-lat_mean)*(i-lat_mean) for i in sample_ary_data['lat'].values])/(len(sample_ary_data)-1))

#lon lat的协方差
x=sample_ary_data['lon'].values
y=sample_ary_data['lat'].values
print(sum([(k[0]-lon_mean)*(k[1]-lat_mean) for k in zip(x,y)])/(len(sample_ary_data)-1))

plt.rcParams['font.sans-serif'] = ['SimHei']  # 解决中文显示问题-设置字体为黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
ax=sample_ary_data.plot(kind='scatter', x="lon",y='lat',s=1,c='g',alpha = 0.7,figsize=(10,10))  #, marker='^'
plt.title('多元正态分布')
plt.show()

norm.rvs生成1个1维的正态分布 

from scipy.stats import norm  # 提供高斯噪声
LEN = len(sample_ary_data)
bias1 = norm.rvs(scale=1, size=2 * LEN)
std=sum([(i-0)*(i-0) for i in bias1])/(2 * LEN-1)
print(std)
plt.plot(bias1)

背景知识：

均值、方差、标准差、协方差，相关系数

标准差：

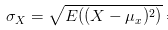
协方差：

相关系数：就是用X、Y的协方差除以X的标准差和Y的标准差。相关系数也可以看成协方差：一种剔除了两个变量量纲影响、标准化后的特殊协方差。

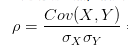
最后

以上就是大胆御姐为你收集整理的random.multivariate_normal和norm.rvs的全部内容，希望文章能够帮你解决random.multivariate_normal和norm.rvs所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。