逻辑回归(Logistic回归)学习小记

逻辑回归(Logistic回归)

优缺点

• 优点：计算代价不高，易于理解和实现
• 缺点：容易欠拟合，分类精度可能不高
• 使用数据类型：数值型和标称型数据

一般过程

• 1、收集数据：任意方法
• 2、准备数据：由于需要进行距离运算，所以数据需要是数值型。另外，结构化数据格式最佳
• 3、分析数据：任意方法
• 4、训练算法：大部分时间将用于训练，训练的目的是为了找到最佳的分类回归系数
• 5、测试算法：训练完成后，此步骤很快
• 6、使用算法：首先，我们需要输入一些数据，并将其转化成对应的结构化数值；接着，基于训练好的回归系数就可以对这些数值进行简单的回归计算，判定他们属于哪个类别；在这之后，我们就可以在输出的类别上做一些其他的分析工作

各种前要知识

Sigmoid函数(逻辑斯蒂函数，S性函数)

//下面先考虑两类问题，且考虑的是判别式函数（判断你是哪一类）
$$\sigma (z)=\frac{1}{1+e^{-z}}=\frac{e^z}{1+e^z}$$

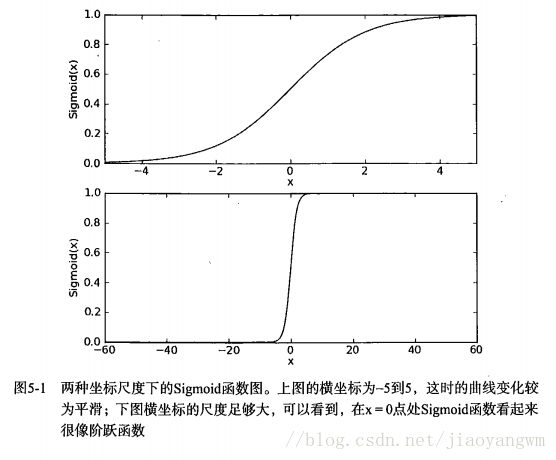
随着z的值增大，Sigmoid将逼近1；随着z的值减小,Sigmoid将逼近0

贝叶斯规则

$$P(A|a)=\frac{P(A)P(a|A)}{P(a)}$$

P(A|a)是后验概率，即a发生了，a属于A的概率。P(A)和P(a)是先验概率，是A，a发生的概率。

P(a|A)是类似然或类条件概率，即在A中a发生的概率。

知道了后验概率就能对某一样本进行分类，后验概率越大，属于这个样本的概率就越大

来源(下面会讲具体来源)

根据一大波公式计算得到{% raw %}$ln(\frac{P(C1|x)}{P(C2|x)})=w^{T}x+w_0$ {% endraw %}

$w和w_0$都是些奇怪的东西，因为P(C1|x)=1-P(C2|x)（在两类问题中），然后就能得到

$P(C1|x)=sigmoid(w^{T}x+w_0)=\frac{1}{1+e^{-(w^{T}x+w_0)}}$

性质

• 1、$lim_{z->+∞}=1 $ 相反等于0

• 2、$\delta (z{)}^{\prime }=\delta (z)[1-\delta (z)]$

• 3、假定二分类训练集{x,y}，x是m维的样本特征向量，y是0或者1

  $P(y=1|x)=p(x)=\frac{1}{1+e^{-w^{T}x+w0}}；P(y=0|x)=1-p(x)=\frac{1}{e^{w^{T}x+w0}}$(w定义往下看)

• 条件的发生概率与不发生概率之比:$\frac{p(x)}{1-p(x)}=e^{w^{T}x+w0}$

• 上式两边同时取对数：$logit(x)=w^{T}x+w0$

如何实现Logistic回归分类器

在每个特征上都乘以一个回归系数，然后将所有的结果值相加，将这个总和带入sigmoid函数中，进而得到一个范围在0~1中的数值，任何大于0.5的数据被分入1类，小于0.5的被分入0类，所以Logistic回归也可以被看成一种概率估计。

分类器的函数形式确定后，问题转化成最佳回归系数是多少？

就是，概率分布形式已有(模型已有)

极大似然估计

来源

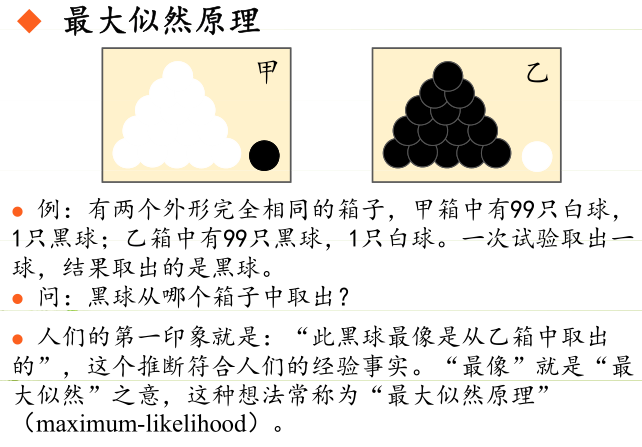
目的

目的：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

常用策略是先假定具有某种确定的概率分布形式，再基于训练样本对概率分布的参数进行估计

流程

类别c的类条件概率为$P(x|c)$,假设$P(x|c)$有确定的形式且被参数向量${\theta }_c$唯一确定，则我们用训练集D估计参数${\theta }_c$,为明确我们记$P(x|c)=P(x|{\theta }_c)$

令$D_c$是训练集D的第c类样本组成的集合，假设这些样本是独立同分布的，则参数值${\theta }_c$对于数据集$D_c$的似然就是
$$P(D_c|{\theta }_c)=\prod _{x\in D_c}P(x|{\theta }_c)$$
为了防止连乘造成下溢(精度误差)，则用对数的形式
$$LL({\theta }_c)=\sum _{x\in D_c}ln(P(x|{\theta }_c))$$

对${\theta }_c$进行极大似然估计，就是去寻找最大化似然$P(D_c|{\theta }_c)$的值的参数$\hat{\theta }$ 。直观上看，最大似然估计在众多参数中试图找一个参数，是的D的出现概率最大，就是找个参数使得D最像是抽取出的

$$\hat{\theta }=argmaxLL(\theta )$$

argmax返回最大值的时候的参数

这个方法得到的是参数，这个参数是使得从数据中抽取一个集合D，它的概率是最像的，样本趋近于无限多的时候，它会趋近于真实值

例：

• 伯努利密度(两类问题)

概率值为p，事件要么发生要么不发生。

内容：若事件发生，x=1；若事件不发生，x=0
$$P(x)=p^x(1-p{)}^{1-x}$$
P(x)就是上面的内容的数学式子

{% raw %}从数据集中取出样本D，D中有N个元素，每个元素对应的x值为$x^t属于0,1$
$$LL(p|D)=ln\prod _{t=1}^N{p}^{(x^t)}(1-p{)}^{(1-x^t)}=\sum _t{x}^{t}lnp+(N-\sum _t{x}^t)ln(1-p)$$
通过对上面的式子求导，使导数=0求得$\hat{p}$
$$LL(p|D{)}^{\prime }=\frac{\sum x^t}{p}-\frac{N-\sum x^t}{1-p}=\frac{\sum x^t-pN}{p(1-p)}$$
{% endraw %}

使上式等于0求得$\hat{p}=\frac{\sum x^t}{N}$ ，$\hat{p}$是事件发生次数和试验次数的比值

式子只有唯一的参数p，这个参数p的估计值(我们用极大似然估计求到的)就是$\hat{p}$ ，$\hat{p}$是事件发生次数和试验次数的比值。从实际的角度来看这的确是p的估计值。

注意，这个估计是样本的函数，也是一个随机变量。抽出不同的Di，可以讨论${\hat{p}}_i$的分布

• 多项式密度(伯努利分布的推广)

随机事件的结果不是两种状态，而是K中互斥，满足${\sum }_{i=1}^K{p}_i=1$

内容：设$x_i$为指示变量，输出为状态i是$x_i=1$，否则为0
$$P(x_1,x_2,...,x_K)=\prod _{i=1}^K{p}_i^{x_i}$$
假定我们做N此这样的独立实验，结果为$D=x^t(t=1-->N)$，其中$x_i^t=1(如果实验t选择状态i)；0(否则)$

其中${\sum }_i{x}_i^t=1$，$p_i$的极大似然估计是${\hat{p}}_i=\frac{{\sum }_t{x}_i^t}{N}$

从实际的角度来看这的确是 $p_i$的估计值。

• 高斯(正态)密度

$$p(x)=\frac{1}{\sqrt{2\pi }\sigma }ln[-\frac{(x-\mu {)}^2}{2{\sigma }^2}],x\in (-\infty ,+\infty )$$

从中选取样本D，其中$x^{t}N(\mu ,{\sigma }^2)$，高斯样本的对数似然为
$$LL(\mu ,\sigma |D)=-\frac{N}{2}ln(2\pi )-Nln(\sigma )-\frac{\sum (x^t-\mu {)}^2}{2{\sigma }^2}$$
通过求该函数的偏导数并使它们等于0，得
$$\hat{\mu }=\frac{\sum x^t}{N}，{\hat{\sigma }}^2=\frac{\sum (x^t-\hat{\mu }{)}^2}{N}$$
通过这个例子能更好的理解极大似然估计

逻辑回归两类问题的极大似然

假定对数似然比是线性的$z=w_0^o+w1x1+w2x2....wnxn=w^{T}x+w_0^o=ln(\frac{p(x|C1)}{p(x|C2)})$

特别的求出了系数w后，使z=0，则可以画出分割线，因为在线上p(x|C1)=p(x|C2)

但是我们要估计的是$P(C1|x)$

根据贝利叶规则
$$ln(\frac{P(C1|x)}{P(C2|x)})=ln(\frac{P(C1|x)}{1-P(C2|x)})=ln(\frac{p(x|C1)}{p(x|C2)})+ln(\frac{P(C1)}{P(C2)})=w^{T}x+w_0(上下两个不是同一个w)$$
整理后就有上面Sigmoid的东西

$w^T$与p的关系$ln(\frac{p(x_i)}{1-p(x_i)})=w^T{x}_i+w0$

下面把每个(x,y)样本前面多加一个1变成(1,x,y)，把w0归入w

有n个独立的训练样本{(x1,y1),…,(xn,yn)},y={0,1}，那么

如果yi=0,P(yi=0|xi)=1-P(yi=1|xi)
$$l(w)=\prod P(y_i=1|x_i{)}^{y_i}[1-P(y_i=1|x_i){]}^{1-y_i}$$
它的对数似然：
$$LL(w)=\sum _{i=1}^n[y_{i}ln(p(x_i))+(1-y_i)ln(1-p(x_i))]$$

$$=\sum _{i=1}^n[y_i[ln(p(x_i))-ln(1-p(x_i))]+ln(1-p(x_i))]$$

$$=\sum _{i=1}^n[y_{i}ln(\frac{p(x_i)}{1-p(x_i)})-ln(1+\frac{p(x_i)}{1-p(x_i)})]$$

$ln(\frac{p(x_i)}{1-p(x_i)})=w^T{x}_i$，然后解得$p(x_i)=\sigma (w^T{x}_i)=\frac{1}{1+e^{-w^T{x}_i}}$

$$=\sum _{i=1}^n{y}_i{w}^T{x}_i-\sum _{i=1}^{n}ln(1+e^{w^t{x}_i})$$

p(小p)和P(大P)的关系上面sigmoid有讲，现在就是要求参数向量w了，求导(把x看成整体，而不是函数)
$$LL(w{)}^{\prime }=\sum _{i=1}^n{x}_i{y}_i-\sum _{i=1}^n\frac{e^{w^T{x}_i}}{1+e^{w^T{x}_i}}{x}_i$$

$$=\sum _{i=1}^n(y_i-\frac{1}{1+e^{-w^T{x}_i}})x_i$$

$$=\sum _{i=1}^n[y_i-\sigma (w^T{x}_i)]x_i$$

使导数等于0，发现无法得到解析解。但因为$y_i-\sigma (w^T{x}_i)$是线性分类器的误差函数，可以通过梯度下降迭代求解式子的近似结果

梯度下降法

梯度下降法又称最速下降法(最优化领域的最简单的算法)

• 流程：梯度法利用一阶梯度信息，逐步找到函数的最优解。梯度下降法是一种迭代算法，选取最优的初值$x^{(0)}$，反复迭代，不断的更新x的值，进行函数目标的及消化，直至收敛

由于梯度方向是函数增长最快的方向，因此负梯度的方向是函数作为极小化的下降方向，所以每一步用负梯度方向来更新x的值(简单的来说就是爬山算法，普通的梯度下降法只能找到极小值，不能找到最小值)

…//不想书上那么多废话了

设置一个步长${\lambda }_k$即学习率，负梯度方向$p^k$，每次更新为$x^{(k+1)}=x^{(k)}+{\lambda }_k{p}_k$，直至导数为0（一个很显然的算法）

综上所述

$\alpha$定义为步长(学习率)

极大似然估计是求最大值，所以梯度下降要改成剃度上升(就是符号变了一下)
$$w^{(t+1)}=w^{(t)}+\alpha LL(w{)}^{\prime }=w^{(t)}+\alpha \sum _{i=1}^n[y_i-\sigma (w^T{x}_i)]x_i$$

逻辑回归步骤

• (1)初始化各种参数,w={1,1，…}，步长为$\alpha$
• (2)重复计算下列步骤N次
  • 1、计算样本集的梯度$LL(w{)}^{\prime }$
  • 2、更新w，$w=w-\alpha LL(w{)}^{\prime }$

随机梯度下降法

梯度下降法是每次用所有数据来迭代更新，这样虽精确但效率低

随机梯度下降飞：每次只用一个数据来迭代更新，搞完这个数据把所有的系数还原，再来一次。显然这样很快，但是精确度不高。

改进版：每次迭代的时候调整一下步长，防止收敛的过快

牛顿法(牛顿迭代)

在x=x0处一阶泰勒展开$f(x)=f(x0)+f^{\prime }(x0)(x-x0)$（近似相等）

求解方程，当f(x)=0时$x=x1=x0-\frac{f(x0)}{f^{\prime }(x0)}$利用近似相等可以是x1离根更近，通过迭代必然会在f(xn)的时候收敛

于是迭代公式$x_{n+1}=x_n-\frac{f(x_n)}{f^{\prime }(x_n)}$

然后套用上面的东西就行了

Python实现(并输出分割线)

由于下面weights矩阵是(n*1)的，所以下面是否转置的地方和上面的公式不一样

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
def loadDataSet():
    dataMat=[]
    labelMat=[]
    fr=open('testSet.txt')
    for line in fr.readlines():
        lineArr=line.strip().split()
        dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    fr.close()
    return dataMat,labelMat
def sigmoid(inX):
    return 1.0/(1+np.exp(-inX))
"""
如下：梯度上升算法,就是求最大值，与梯度下降相反
"""
def gradAscent(dataMatln,classLabels):
    dataMatrix=np.mat(dataMatln)
    labelMat=np.mat(classLabels).transpose()
    m,n=np.shape(dataMatrix)
    alpha=0.001
    maxCycles=500
    weights=np.ones((n,1))
    for k in range(maxCycles):
        h=sigmoid(dataMatrix*weights)
        error=labelMat-h
        weights=weights+alpha*dataMatrix.transpose()*error
    return weights.getA()
def plotBestFit(weights):
    dataMat,labelMat=loadDataSet()
    dataArr=np.array(dataMat)
    n=np.shape(dataMat)[0]
    xcord1=[];ycord1=[]
    xcord2=[];ycord2=[]
    for i in range(n):
        if int(labelMat[i])==1:
            xcord1.append(dataArr[i,1])
            ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1])
            ycord2.append(dataArr[i,2])
    fig=plt.figure()
    ax=fig.add_subplot(111)
    ax.scatter(xcord1,ycord1,s=20,c='red',marker='s',alpha=.5)
    ax.scatter(xcord2,ycord2,s=20,c='green',alpha=.5)
    x=np.arange(-3.0,3.0,0.1)
    y=(-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x,y)
    plt.title('DataSet')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()
if __name__=='__main__':
    dataMat,labelMat=loadDataSet()
    weights=gradAscent(dataMat,labelMat)
    print(weights)
    plotBestFit(weights)

最后

以上就是天真悟空为你收集整理的逻辑回归(Logistic回归)学习小记的全部内容，希望文章能够帮你解决逻辑回归(Logistic回归)学习小记所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。