在此讲一下logistic回归中cost函数的推导过程
在此之前,先回顾一下Logistic回归。
Logistic回归
基本原理:“回归”就是用一条直线对一堆数据点进行拟合,这个拟合过程就称为“回归”。利用Logistic回归进行分类的主要思想是,根据现有数据对分类边界线建立回归公式,以此进行分类。
以Andrew公开课的例子说明:
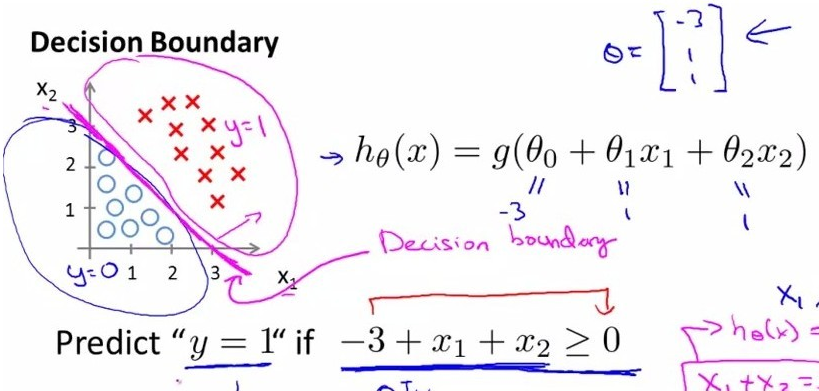
圆(蓝色)和叉(红色)是两类数据点,我们需要找到一个决策边界将其划分开,如图所示的边界形式显然是线性的形式,如图中所描述的:
我们记为:
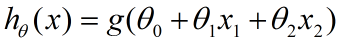
这里,括号里的就是决策边界的表达式,我们找一个函数g,将表达式结果作为输入,生成一个预测函数hθ(x).这里我们使用Sigmoid函数
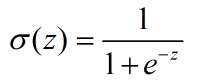
从而:
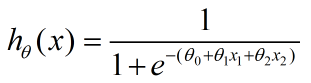
然而有时候,决策边界用一维直线无法区分,也就是这里的θ参数个数是变数,比如下面这堆数据

这是一种非线性的决策边界。
可以看到这里,将x1,x2参数全部平方处理,找得一个圆形边界。
公式推导
讲到这里,我们可以把边界形式做如下推广:
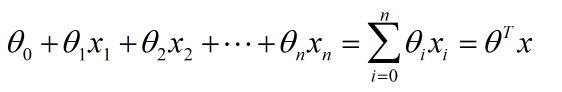
边界的最后一项是向量相乘的形式,即:

将其输入到sigmoid函数去判断其所属类别,就有了我们的预测函数,记为:
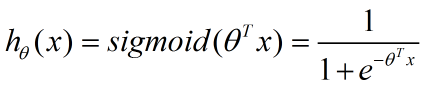
根据sigmoid图像,这个预测函数输出值大于0.5,那么代表x(数据点)所属类别为1,否则是0(对于二分类问题)。
但是别忘了我们的最初的目标,这里的θ向量未知。我们的目的是:
确定θ的参数值,使得我们这个决策边界能更好地划分数据集。
这个过程,在Andrew的课程里,被略过了,他直接给出了cost函数和J(θ)函数,然后通过梯度下降求得最优的θ参数。其中,J(θ)函数是这样的:
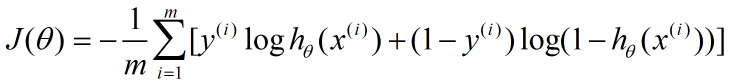
利用上面的公式以及梯度下降算法,我们就能求出θ的值。也就能求出最能拟合数据的决策边界。
接下来就要讲讲这个公式是怎么被推导出来的。
我们先来看看现在我们已经知道什么:
1、一堆数据点+它们的类别(2类)
2、它们的概率分布hθ(x):虽然目前θ仍然是未知参数
我们的目标是求出未知参数,使得每个样本数据点属于它当前所标记的类别的概率最大。
于是就引出了Fisher的极大似然估计。
这里就不讲极大似然估计的具体概念和公式推导了,不过还是用个例子来形象的说明极大似然估计的作用吧:
一个猎人和一个学生一起走在山路上,突然从山间跑出一只兔子,啪一声枪响,兔子倒地而亡。问:谁最有可能杀死了兔子?
答案显而易见:猎人。那么这里,猎人就是那个参数θ。极大似然估计的目标就是预测出待估参数,使得样本事件发生的概率最大。
对于上述例子,用极大似然估计的思想来说明其中的几个重要信息:
| 样本事件 | 兔子被枪杀 |
| 待估参数 | 射死了兔子的人(记为θ:θ属于{猎人,学生}) |
极大似然估计就是找出最有可能杀死兔子的人。
同样,对于本实验的一堆数据点,我们对应着看:
| 样本事件 | 每个样本数据点属于他自己的label |
| 待估参数 | 决策边界参数向量θ |
P.S.虽然样本里的每条数据都表明了数据点本身的类别,但是使用极大似然估计的时候,你并不知道样本本身所属的类别,样本数据自带的类别标签是你估计好坏的一个评价标准。换句话说,数据点全体就是一个样本事件
接下来就是估计所需要的数学推导了。
对于一个连续性的分布,我们需要它的概率密度函数,在本例中,其实就是那个sigmoid函数(取值范围0-1刚好表示的是发生概率),我们重新写在这里:
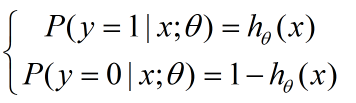
把这两个式子写在一起:
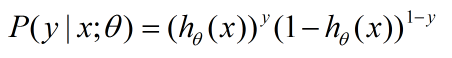
可以验证一下,当y=1或者y=0的时候,上式分别满足上上式。对每个样本数据点,满足上式,所以对于群体,我们接下来继续。
根据极大似然估计的求解步骤,取似然函数:
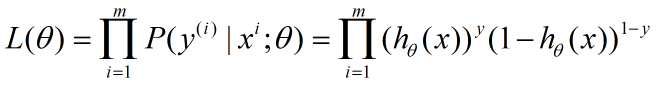
要求L(θ)的最大值对应的θ参数。其中m是样本数据点的个数
连乘不容易求解,同时又容易造成下溢出。这里由于x和ln(x)单调性相同,两边取对数
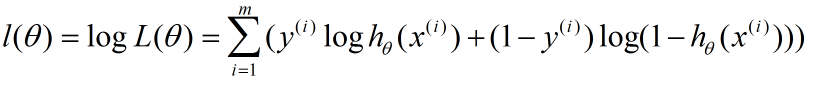
这个就是Andrew给的那个J(θ)了,唯一的区别就是,Andrew在前面乘了一个负系数,使得这里求最大值变成了最小值,从而可以使用梯度下降算法。
不过其实用本式也可以完成任务,只是用的算法就变成梯度上升了,其实没有区别。
最后
以上就是飞快火车最近收集整理的关于logistic回归中cost函数J(θ)的公式推导的全部内容,更多相关logistic回归中cost函数J(θ)内容请搜索靠谱客的其他文章。








发表评论 取消回复