随机变量
随机变量 x mathbf{x} x是对每个结果 ξ xi ξ制定⼀个数 x ( ξ ) mathbf{x}(xi) x(ξ)的过程。随机变量量本质上是个函数。从数映射到事件的函数。
我们可以从量纲来思考一个量的物理意义,但是 x mathbf{x} x没有量纲, x mathbf{x} x的取值与事件之间的映射关系也可能是不确定的。
x mathbf{x} x属于一个事件空间,该空间包含了所有可能事件,该空间可以是连续的也可以是离散的。
分布函数(cumulative distribution function)
F x ( x ) = P { x ≤ x } F_{x}(x)=P{mathbf{x} leq x} Fx(x)=P{x≤x}
-
函数 F ( x ) F(x) F(x) 是右连续的,即 F ( x + ) = F ( x ) Fleft(x^{+}right)=F(x) F(x+)=F(x)
-
P { x 1 < x ≤ x 2 } = F ( x 2 ) − F ( x 1 ) Pleft{x_{1}<mathrm{x} leq x_{2}right}=Fleft(x_{2}right)-Fleft(x_{1}right) P{x1<x≤x2}=F(x2)−F(x1)
-
P { x 1 ≤ x ≤ x 2 } = F ( x 2 ) − F ( x 1 − ) Pleft{x_{1} leq mathrm{x} leq x_{2}right}=Fleft(x_{2}right)-Fleft(x_{1}^{-}right) P{x1≤x≤x2}=F(x2)−F(x1−)
-
P { x = x } = F ( x ) − F ( x − ) P{mathrm{x}=x}=F(x)-Fleft(x^{-}right) P{x=x}=F(x)−F(x−)
-
分位点(percentile)
一个随机变量 x mathbf{x} x的分位点是满足 u = P { x ≤ x u } = F ( x u ) u=Pleft{mathbf{x} leq x_{u}right}=Fleft(x_{u}right) u=P{x≤xu}=F(xu)的最小实数 x u x_{u} xu
概率密度函数(probability density function,p.d.f)
f x ( x ) = d F x ( x ) d x f_{x}(x) = frac{mathrm{d} F_{x}(x)}{mathrm{d} x} fx(x)=dxdFx(x)
概率质量函数(probability mass function,p.m.f)
是离散随机变量在各特定取值上的概率。
-
概率质量函数和概率密度函数不同之处:
-
概率质量函数是对离散随机变量定义的,本身代表该值的概率;
-
概率密度函数是对连续随机变量定义的,本身不是概率,只有对连续随机变量的概率密度函数在某区间内进行积分后才是概率。
-
常用的随机变量量
连续型随机变量量
-
均匀分布
f ( x ) = { 1 b − a for a ≤ x ≤ b 0 elsewhere f(x)=left{begin{array}{cc} frac{1}{b-a} & text { for } a leq x leq b \ 0 & text { elsewhere } end{array}right. f(x)={b−a10 for a≤x≤b elsewhere
在误差分析时经常遇到均匀分布,如数字信号中的量化噪声。由于 A/D 转换器的字长有限,模拟信号通过A/D转换时,势必要舍弃部分信息。丢失信息后相当于使信号附加了一部分噪声,称为量化噪声。量化噪声分为截尾噪声和舍入噪声,它们都是均匀分布的,且方差相同,不同的是分布的区间。 -
正态分布
高斯白噪声,有多重要就不多说了。
f ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x)=frac{1}{sigma sqrt{2 pi}} e^{-frac{(x-mu)^{2}}{2 sigma^{2}}} f(x)=σ2π1e−2σ2(x−μ)2
在实际应用中,许多独立噪声之和若满足中心极限定理中某一定理的条件,就认为是高斯分布的。一般情况下,不同分布律的随机变量之和趋向高斯分布的速度是不同的 。在工程上,如果不是某个或某些随机变量对和的贡献很大,7~10 个随机变量之和的分布就认为是高斯分布的。 -
卡方分布
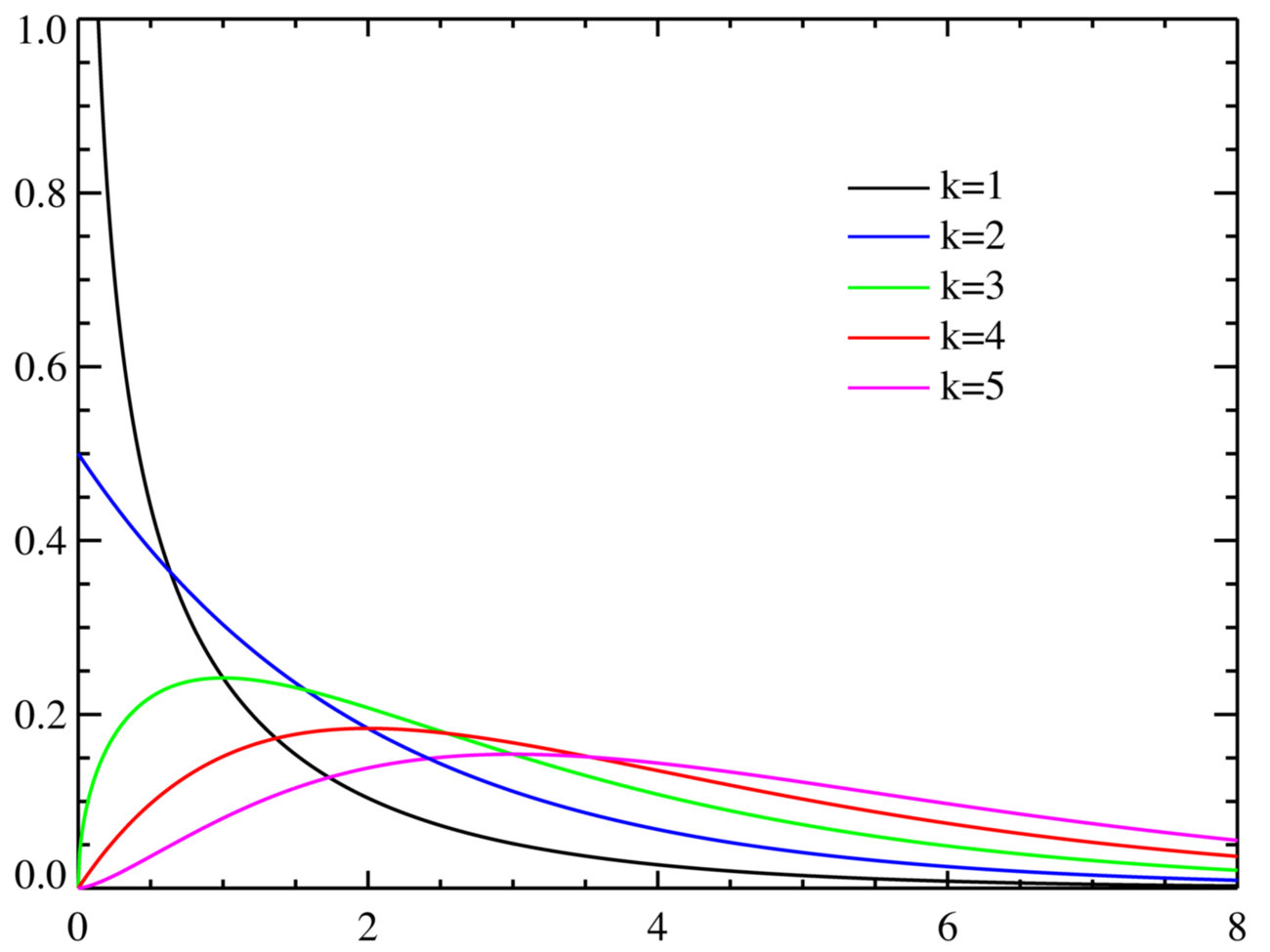
f k ( x ) = 1 2 k 2 Γ ( k 2 ) x k 2 − 1 e − x 2 f_{k}(x)=frac{1}{2^{frac{k}{2}} Gammaleft(frac{k}{2}right)} x^{frac{k}{2}-1} e^{frac{-x}{2}} fk(x)=22kΓ(2k)1x2k−1e2−x
如果为正整数,则:
Γ ( n ) = ( n − 1 ) ! Gamma(n)=(n-1) ! Γ(n)=(n−1)!
对于实数部分为正的复数,伽玛函数定义为:
Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t Gamma(z)=int_{0}^{infty} t^{z-1} mathrm{e}^{-t} mathrm{~d} mathrm{t} Γ(z)=∫0∞tz−1e−t dt
在信号的传输过程中,信号一般是窄带形式,这样不可避免要用到包络检波 。在小信号检波时,通常采用平方律检波,因此检波器输出是信号与噪声包络的平方 。 有时为了使信号检测的错误概率更小,还要对检波器的输出信号进行积累。
如果随机变量 X X X 是高斯分布,那么平方律检波器的输出 X 2 X^{2} X2 是 X 2 mathcal{X}^2 X2分布。若 X i X_{i} Xi 的数学期望为零,则 Y Y Y 为中心 X 2 mathcal{X}^2 X2分布;若 X i X_{i} Xi 的数学期望不为零,则 Y Y Y 为非中心 X 2 mathcal{X}^2 X2分布。
对检波器的输出信号进行采样后积累的信号 Y = ∑ i = 1 n X i 2 Y=sum_{i=1}^{n} X_{i}^{2} Y=∑i=1nXi2是 n n n自由度的 X 2 mathcal{X}^2 X2分布。
-
瑞利分布
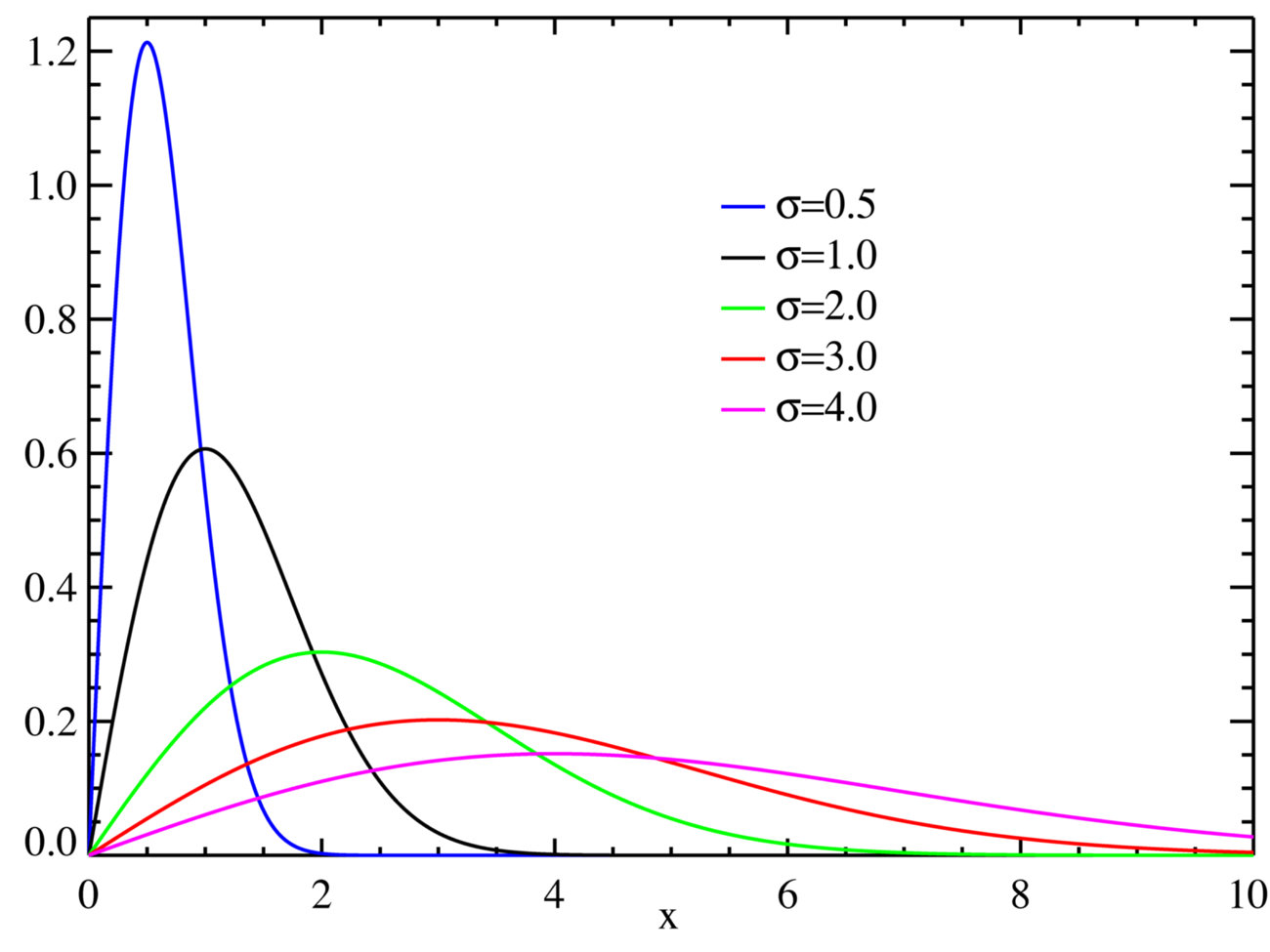
f ( x ; σ ) = x σ 2 e − x 2 / 2 σ 2 , x ≥ 0 f(x ; sigma)=frac{x}{sigma^{2}} e^{-x^{2} / 2 sigma^{2}}, quad x geq 0 f(x;σ)=σ2xe−x2/2σ2,x≥0
当一个随机二维向量的两个分量呈独立的、均值为0,有着相同的方差的正态分布时,这个向量的模呈瑞利分布。
瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型。两个正交高斯噪声信号之和的包络服从瑞利分布。
高斯、莱斯、瑞利,信号很强,瑞利;噪声很强,高斯。
-
Nakagami-m分布
用来对多径·无线·衰弱信道进行建模
离散型随机变量量
-
二项式分布
f ( k , n , p ) = Pr ( X = k ) = C k n p k ( 1 − p ) n − k f(k, n, p)=operatorname{Pr}(X=k)=C_{k}^{n} p^{k}(1-p)^{n-k} f(k,n,p)=Pr(X=k)=Cknpk(1−p)n−k
在信号检测理论中,非参量检测时单次探测的秩值为某一值的概率服从二项式分布。 -
伯努利分布
f X ( x ) = p x ( 1 − p ) 1 − x = { p if x = 1 q if x = 0 f_{X}(x)=p^{x}(1-p)^{1-x}=left{begin{array}{ll} p & text { if } x=1 \ q & text { if } x=0 end{array}right. fX(x)=px(1−p)1−x={pq if x=1 if x=0
伯努利分布是二项分布在n = 1时的特殊情况。 -
泊松分布
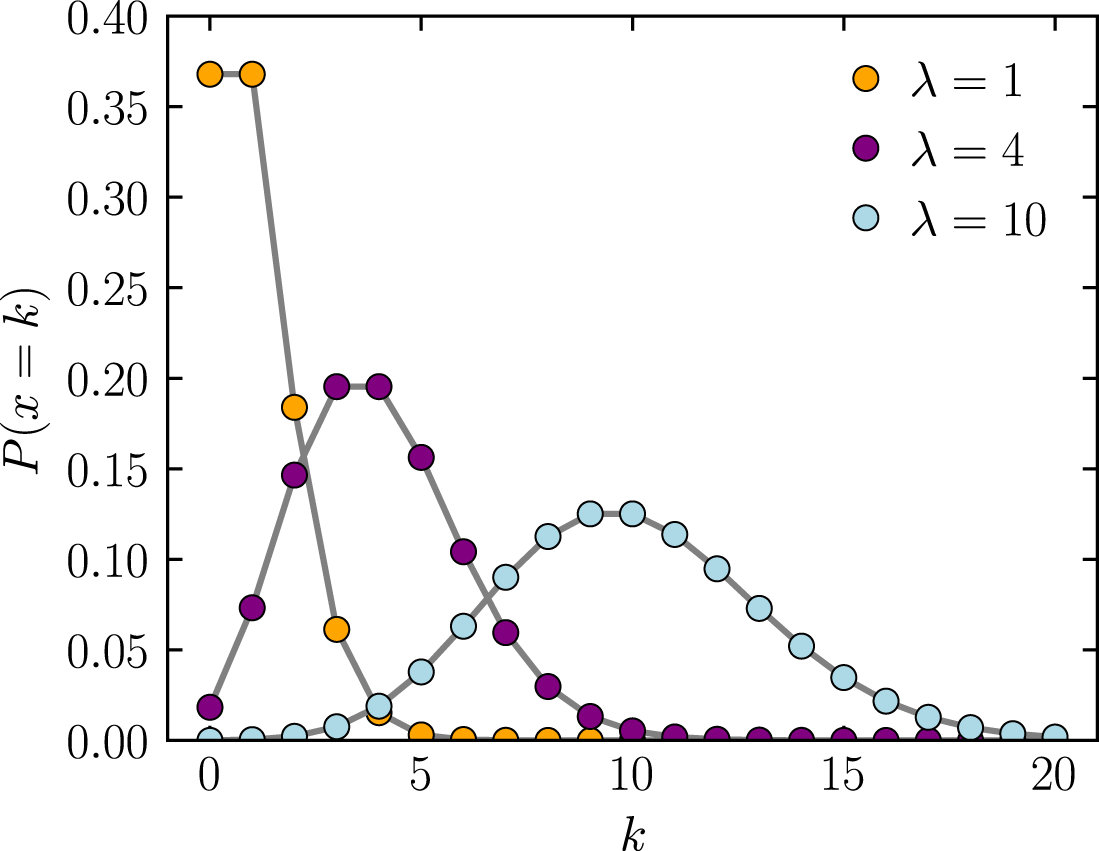 $$ P(X=k)=frac{e^{-lambda} lambda^{k}}{k !} $$ 注:参数$λ$是单位时间(或单位面积)内随机事件的平均发生率。
$$ P(X=k)=frac{e^{-lambda} lambda^{k}}{k !} $$ 注:参数$λ$是单位时间(或单位面积)内随机事件的平均发生率。 泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数等。
随机过程和序列的统计特征
均值(mean,expected value,expectation)
E { x } = ∫ − ∞ ∞ x f ( x ) d x E{mathbf{x}}=int_{-infty}^{infty} x f(x) mathrm{d} x E{x}=∫−∞∞xf(x)dx
E { x } = ∑ i p i x i , p i = P { x = x i } E{boldsymbol{x}}=sum_{i} p_{i} x_{i}, quad p_{i}=Pleft{boldsymbol{x}=x_{i}right} E{x}=i∑pixi,pi=P{x=xi}
方差(variance)
σ 2 = D [ X ] = E { ( x − η ) 2 } = ∫ − ∞ ∞ [ x − m X ] 2 f X ( x ) d x sigma^{2}=D[X]=Eleft{(mathbf{x}-eta)^{2}right}=int_{-infty}^{infty}left[x-m_{X}right]^{2} f_{X}(x) mathrm{d} x σ2=D[X]=E{(x−η)2}=∫−∞∞[x−mX]2fX(x)dx
σ 2 = ∑ i p i ( x i − η ) 2 p i = P { x = x i } sigma^{2}=sum_{i} p_{i}left(x_{i}-etaright)^{2} quad p_{i}=Pleft{x=x_{i}right} σ2=i∑pi(xi−η)2pi=P{x=xi}
矩/动差(moment)
m n = E { x n } = ∫ − ∞ ∞ x n f ( x ) d x m_{n}=Eleft{mathbf{x}^{n}right}=int_{-infty}^{infty} x^{n} f(x) mathrm{d} x mn=E{xn}=∫−∞∞xnf(x)dx
μ n = ∑ i = 1 ∞ ( x i ) n P i , n = 1 , 2 , ⋯ mu_{n}=sum_{i=1}^{infty}left(x_{i}right)^{n} P_{i}, quad n=1,2, cdots μn=i=1∑∞(xi)nPi,n=1,2,⋯
中心矩(Central moments)
μ n = E { ( x − η ) n } = ∫ − ∞ ∞ ( x − η ) n f ( x ) d x mu_{n}=Eleft{(mathbf{x}-eta)^{n}right}=int_{-infty}^{infty}(x-eta)^{n} f(x) mathrm{d} x μn=E{(x−η)n}=∫−∞∞(x−η)nf(x)dx
μ n = ∑ i = 1 ∞ ( x i − E [ X ] ) n P i , n = 1 , 2 , ⋯ mu_{n}=sum_{i=1}^{infty}left(x_{i}-E[X]right)^{n} P_{i}, quad n=1,2, cdots μn=i=1∑∞(xi−E[X])nPi,n=1,2,⋯
- 第0阶中心矩 μ 0 mu_{0} μ0 恒为1。
- 第1阶中心矩 μ 1 mu_{1} μ1 恒为0。
- 第2阶中心矩 μ 2 mu_{2} μ2 为 X X X 的方差 Var ( X ) operatorname{Var}(X) Var(X)
- 第3阶中心矩 μ 3 mu_{3} μ3 用于定义 X X X 的偏度。
偏度/歪度(Skewness),在概率论和统计学中衡量实数随机变量概率分布的不对称性。
γ 1 = E [ ( X − μ σ ) 3 ] = μ 3 σ 3 gamma_{1}=mathrm{E}left[left(frac{X-mu}{sigma}right)^{3}right]=frac{mu_{3}}{sigma^{3}} γ1=E[(σX−μ)3]=σ3μ3
偏态系数/偏差系数(deviation coefficient),说明随机系列分配不对称程度的统计参数。
变异系数/离散系数/变差系数(coefficient of variation),是概率分布离散程度的一个归一化量度,其定义为标准差 σ sigma σ与平均值 μ mu μ之比
- 第4阶中心矩 μ 4 mu_{4} μ4 用于定义 X X X 的峰度。
峰度/尖度(Kurtosis),在统计学中衡量实数随机变量概率分布的峰态。峰度系数越大,分布就有更多的极端值,那么其余值必然要更加集中在众数周围,其分布必然就更加陡峭。

- 中心矩具有平移不变性。对于任意的随机变量 X X X 和任意常数 c , c, c, 恒有: μ n ( X + c ) = μ n ( X ) mu_{n}(X+c)=mu_{n}(X) μn(X+c)=μn(X)
- n阶中心矩是n次齐次函数。 μ n ( c X ) = c n μ n ( X ) mu_{n}(c X)=c^{n} mu_{n}(X) μn(cX)=cnμn(X)
- 只有当 n ∈ { 1 , 2 , 3 } , n in{1,2,3}, n∈{1,2,3}, 且 X X X 和 Y Y Y 为两个互相独立的随机变量时,中心矩才具有加法性。 μ n ( X + Y ) = μ n ( X ) + μ n ( Y ) mu_{n}(X+Y)=mu_{n}(X)+mu_{n}(Y) μn(X+Y)=μn(X)+μn(Y)
特征函数(eigenfunction)
Φ x ( ω ) = E { e j ω x } = ∫ − ∞ ∞ f ( x ) e j ω x d x Phi_{x}(omega)=Eleft{e^{j omega mathbf{x}}right}=int_{-infty}^{infty} f(x) e^{j omega x} mathrm{~d} x Φx(ω)=E{ejωx}=∫−∞∞f(x)ejωx dx
-
∣ Φ x ( ω ) ∣ ≤ Φ ( 0 ) = 1 left|Phi_{x}(omega)right| leq Phi(0)=1 ∣Φx(ω)∣≤Φ(0)=1
-
若 y = a x + b , mathbf{y}=a mathbf{x}+b, y=ax+b, 则 Φ y ( ω ) = e j b ω Φ x ( a ω ) Phi_{y}(omega)=e^{j b omega} Phi_{x}(a omega) Φy(ω)=ejbωΦx(aω)
-
f ( x ) = 1 2 π ∫ − ∞ ∞ Φ x ( ω ) e − j ω x d x f(x)=frac{1}{2 pi} int_{-infty}^{infty} Phi_{x}(omega) e^{-j omega x} mathrm{~d} x f(x)=2π1∫−∞∞Φx(ω)e−jωx dx
矩生成函数(moment generating function)
Φ ( s ) = ∫ − ∞ ∞ f ( x ) e s x d x mathbf{Phi}(s)=int_{-infty}^{infty} f(x) e^{s x} mathrm{~d} x Φ(s)=∫−∞∞f(x)esx dx
矩定理
Φ ( n ) ( s ) = E ( x n e s x ) Φ ( n ) ( 0 ) = E ( x n ) = m n begin{array}{c} mathbf{Phi}^{(n)}(s)=Eleft(mathbf{x}^{n} e^{s mathbf{x}}right) \ mathbf{Phi}^{(n)}(0)=Eleft(mathbf{x}^{n}right)=m_{n} end{array} Φ(n)(s)=E(xnesx)Φ(n)(0)=E(xn)=mn
Φ ( s ) mathbf{Phi}(s) Φ(s) 在原点的各阶导数等于 x boldsymbol{x} x 的各阶矩。这说明了为什么把 Φ ( s ) mathbf{Phi}(s) Φ(s) 称为“矩生成函数”。
当各阶矩都有限并且级数在 s = 0 s = 0 s=0附近绝对收敛时,如果随机变量的各阶矩已知,其分布密度就被惟一确定。
第二特征函数(eigenfunction)
Ψ ( ω ) = ln Φ x ( ω ) = Ψ ( j ω ) Psi(omega)=ln Phi_{x}(omega)=mathbfPsi(j omega) Ψ(ω)=lnΦx(ω)=Ψ(jω)
累积量(cumulants)
一个随机变量的累积量是指一系列能够提供和“矩”一样的信息的量。
λ
n
=
d
n
Ψ
(
s
)
d
s
n
lambda_{n}=frac{mathrm{d}^{n} boldsymbol{Psi}(s)}{mathrm{d} s^{n}}
λn=dsndnΨ(s)
对于随机变量 X X X 而言,一阶累积量等于期望值 E ( x ) E(x) E(x), 二阶累积量等于方差 V ( x ) V(x) V(x) ,三阶累积量等于三阶中心矩 S ( x ) S(x) S(x) ,但是四阶以及更高阶的累积量与同阶的中心矩并不相等。
在某些理论推导中,使用累积量更加方便。特别是当两个或者更多的随机变量相互独立时, 它们的 n n n 阶累积量的和等于它们和的 n n n 阶累积量。
服从正态分布的随机变量的三阶及以上的累积量为 0 0 0
另:条件分布
条件概率
F ( x ∣ M ) = P { x ≤ x ∣ M } = P { x ≤ x , M } P ( M ) F(x mid M)=P{mathbf{x} leq x mid M}=frac{P{mathbf{x} leq x, M}}{P(M)} F(x∣M)=P{x≤x∣M}=P(M)P{x≤x,M}
条件密度
f ( x ∣ M ) = d F ( x ∣ M ) d x f(x mid M)=frac{mathrm{d} F(x mid M)}{mathrm{d} x} f(x∣M)=dxdF(x∣M)
全概率定理理
∫ − ∞ ∞ P ( A ∣ x = x ) f ( x ) d x = P ( A ) int_{-infty}^{infty} P(A mid mathbf{x}=x) f(x) mathrm{d} x=P(A) ∫−∞∞P(A∣x=x)f(x)dx=P(A)
贝叶斯定理理
f ( x ∣ A ) = P ( A ∣ x = x ) P ( A ) f(x mid A)=frac{P(A mid mathbf{x}=x)}{P(A)} f(x∣A)=P(A)P(A∣x=x)
f ( x ) = P ( A ∣ x = x ) f ( x ) ∫ − ∞ ∞ P ( A ∣ x = x ) f ( x ) d x f(x)=frac{P(A mid mathbf{x}=x) f(x)}{int_{-infty}^{infty} P(A mid mathbf{x}=x) f(x) mathrm{d} x} f(x)=∫−∞∞P(A∣x=x)f(x)dxP(A∣x=x)f(x)
条件均值
E ( x ∣ M ) = ∫ − ∞ ∞ x f ( x ∣ M ) d x E(mathbf{x} mid M)=int_{-infty}^{infty} x f(x mid M) mathrm{d} x E(x∣M)=∫−∞∞xf(x∣M)dx
另:复合函数 y = g ( x ) y = g(x) y=g(x)
基本定理
对于给定的
y
y
y, 要找出
f
y
(
y
)
,
f_{y}(y),
fy(y), 首先需要解方程
y
=
g
(
x
)
y=g(x)
y=g(x) 。用
x
n
x_{n}
xn 来表示它的实根
y
=
g
(
x
1
)
=
⋯
=
g
(
x
n
)
y=gleft(x_{1}right)=cdots=gleft(x_{n}right)
y=g(x1)=⋯=g(xn)
则
f
y
(
y
)
=
f
x
(
x
1
)
∣
g
′
(
x
1
)
∣
+
⋯
+
f
x
(
x
n
)
∣
g
′
(
x
n
)
∣
+
⋯
f_{y}(y)=frac{f_{x}left(x_{1}right)}{left|g^{prime}left(x_{1}right)right|}+cdots+frac{f_{x}left(x_{n}right)}{left|g^{prime}left(x_{n}right)right|}+cdots
fy(y)=∣g′(x1)∣fx(x1)+⋯+∣g′(xn)∣fx(xn)+⋯
均值
E ( g ( x ) ) = ∫ − ∞ ∞ g ( x ) f x ( x ) d x E(g(mathbf{x}))=int_{-infty}^{infty} g(x) f_{x}(x) mathrm{d} x E(g(x))=∫−∞∞g(x)fx(x)dx
二元随机变量
联合分布(Joint Distribution)
F ( x , y ) = P { x ≤ x , y ≤ y } F(x, y)=P{mathbf{x} leq x, mathbf{y} leq y} F(x,y)=P{x≤x,y≤y}
- $F(-infty, y)=0 quad F(x,-infty)=0 quad F(infty, infty)=1 $
- $Pleft{x_{1}<mathbf{x} leq x_{2}, mathbf{y} leq yright}=Fleft(x_{2}, yright)-Fleft(x_{1}, yright) $
- $Pleft{mathbf{x} leq x, y_{1}<mathbf{y} leq y_{2}right}=Fleft(x, y_{2}right)-Fleft(x, y_{1}right) $
- $Pleft{x_{1}<mathbf{x} leq x_{2}, y_{1}<mathbf{y} leq y_{2}right}=Fleft(x_{2}, y_{2}right)-Fleft(x_{2}, y_{1}right)-Fleft(x_{1}, y_{2}right)+Fleft(x_{1}, y_{1}right) $
联合分布密度 (Joint Density)
f ( x , y ) = ∂ F ( x , y ) ∂ x ∂ y f(x, y)=frac{partial F(x, y)}{partial x partial y} f(x,y)=∂x∂y∂F(x,y)
协方差(Covariance)
C x y = E { ( x − η x ) ( y − η y ) } C_{x y}=Eleft{left(mathbf{x}-eta_{x}right)left(mathbf{y}-eta_{y}right)right} Cxy=E{(x−ηx)(y−ηy)}
二元随机变量的单个函数 z = g ( x , y ) z = g(x, y) z=g(x,y)
Y=X1 +X2,如果X1和X2互相独立,则 f Y ( y ) = ∫ − ∞ ∞ f X 1 ( x 1 ) f X 2 ( y − x 1 ) d x 1 = f X 1 ( y ) ∗ f X 2 ( y ) f_{Y}(y)=int_{-infty}^{infty} f_{X_{1}}left(x_{1}right) f_{X_{2}}left(y-x_{1}right) mathrm{d} x_{1}=f_{X_{1}}(y) * f_{X_{2}}(y) fY(y)=∫−∞∞fX1(x1)fX2(y−x1)dx1=fX1(y)∗fX2(y)
另:独立、不相关、正交
独立性(Independence)
- $F(x, y)=F_{x}(x) F_{y}(y) $
- f ( x , y ) = f x ( x ) f y ( y ) f(x, y)=f_{x}(x) f_{y}(y) f(x,y)=fx(x)fy(y)
不相关性 (Uncorrelatedness)
- 协方差:$C_{x y}=0 $
- 相关系数: ρ x y = C x y σ x σ y = 0 rho_{x y}=frac{C_{x y}}{sigma_{x} sigma_{y}}=0 ρxy=σxσyCxy=0
- E { x y } = E { x } E { y } E{mathbf{x y}}=E{mathbf{x}} E{mathbf{y}} E{xy}=E{x}E{y}
正交性(Orthogonality)
- 相关矩: E { x y } = 0 E{mathbf{x y}}=0 E{xy}=0
随机过程和序列
随机过程是随时间变化的随机变量。随机过程在一个时刻上则是一个随机变量。
-
需要清楚以下概念:
随机过程、连续随机过程、离散随机过程
随机序列、连续随机序列、离散随机序列
一阶分布函数
F ( x , t ) = P { x ( t ) ≤ x } F(x, t)=P{mathbf{x}(t) leq x} F(x,t)=P{x(t)≤x}
二阶分布函数
F ( x 1 , x 2 ; t 1 , t 2 ) = P { x ( t 1 ) ≤ x 1 , x ( t 2 ) ≤ x 2 } Fleft(x_{1}, x_{2} ; t_{1}, t_{2}right)=Pleft{mathbf{x}left(t_{1}right) leq x_{1}, mathbf{x}left(t_{2}right) leq x_{2}right} F(x1,x2;t1,t2)=P{x(t1)≤x1,x(t2)≤x2}
随机过程和序列的统计特征
期望
m X ( t ) = E [ X ( t ) ] = ∫ − ∞ ∞ x f X ( x , t ) d x m_{X}(t)=E[X(t)]=int_{-infty}^{infty} x f_{X}(x, t) mathrm{d} x mX(t)=E[X(t)]=∫−∞∞xfX(x,t)dx
方差
σ X 2 ( t ) = D [ X ( t ) ] = ∫ − ∞ ∞ [ x − m X ( t ) ] 2 f X ( x , t ) d x sigma_{X}^{2}(t)=D[X(t)]=int_{-infty}^{infty}left[x-m_{X}(t)right]^{2} f_{X}(x, t) mathrm{d} x σX2(t)=D[X(t)]=∫−∞∞[x−mX(t)]2fX(x,t)dx
数学期望和方差描述了随机过程在任意一个时刻t 的集中和离散程度。
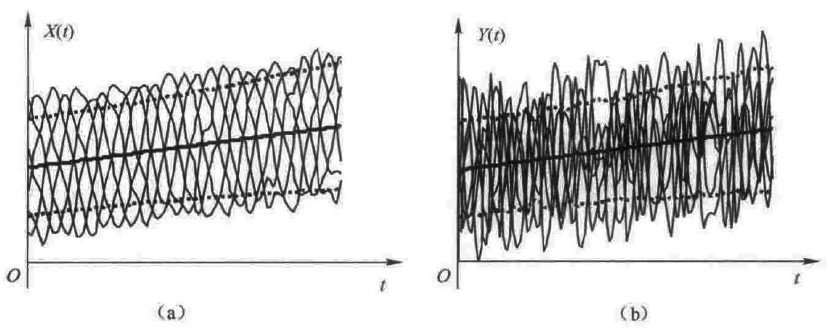
从图上可粗略看出,在任意时刻它们的数学期望和方差都大体相同,但两个随机过程样本函数的内部结构却截然不同。X(t)起伏慢,Y(t) 则起伏较快,这种差异是因为它们的相关性不同造成的。
相关(Correlation)显示了两个或几个随机变量之间线性关系的强度和方向。在统计学中,相关的意义是:用来衡量两个变量相对于其相互独立的距离。在这个广义的定义下,有许多根据数据特点用来衡量数据相关性而定义的系数,称作 相关系数。通常使用相关系数来计量这些随机变量协同变化的程度,当随机变量间呈现同一方向的变化趋势时称为正相关,反之则称为负相关。
相关的概念表征了随机过程在两时刻之间的关联程度,进而说明了随机过程起伏变化的快慢。还隐含着幅度的变化。
自相关函数
R X ( t 1 , t 2 ) = E [ X ( t 1 ) X ( t 2 ) ] = ∫ − ∞ ∞ ∫ − ∞ ∞ x 1 x 2 f X ( x 1 , x 2 ; t 1 , t 2 ) d x 1 d x 2 R_{X}left(t_{1}, t_{2}right)=Eleft[Xleft(t_{1}right) Xleft(t_{2}right)right]=int_{-infty}^{infty} int_{-infty}^{infty} x_{1} x_{2} f_{X}left(x_{1}, x_{2} ; t_{1}, t_{2}right) mathrm{d} x_{1} mathrm{~d} x_{2} RX(t1,t2)=E[X(t1)X(t2)]=∫−∞∞∫−∞∞x1x2fX(x1,x2;t1,t2)dx1 dx2
t 1 = t 2 t_{1}=t_{2} t1=t2时 R X ( 0 ) R_{X}(0) RX(0)表示平均功率
自协方差函数
C X ( t 1 , t 2 ) = E [ { X ( t 1 ) − m X ( t 1 ) } { X ( t 2 ) − m X ( t 2 ) } ] = ∫ − ∞ ∞ ∫ − ∞ ∞ [ x 1 − m X ( t 1 ) ] [ x 2 − m X ( t 2 ) ] f X ( x 1 , x 2 ; t 1 , t 2 ) d x 1 d x 2 begin{aligned} C_{X}left(t_{1}, t_{2}right) &=Eleft[left{Xleft(t_{1}right)-m_{X}left(t_{1}right)right}left{Xleft(t_{2}right)-m_{X}left(t_{2}right)right}right] \ &=int_{-infty}^{infty} int_{-infty}^{infty}left[x_{1}-m_{X}left(t_{1}right)right]left[x_{2}-m_{X}left(t_{2}right)right] f_{X}left(x_{1}, x_{2} ; t_{1}, t_{2}right) mathrm{d} x_{1} mathrm{~d} x_{2} end{aligned} CX(t1,t2)=E[{X(t1)−mX(t1)}{X(t2)−mX(t2)}]=∫−∞∞∫−∞∞[x1−mX(t1)][x2−mX(t2)]fX(x1,x2;t1,t2)dx1 dx2
t 1 = t 2 t_{1}=t_{2} t1=t2时就是方差
自相关函数和协方差函数只相差一个统计平均值: C X ( t 1 , t 2 ) = R X ( t 1 , t 2 ) − m X ( t 1 ) m X ( t 2 ) C_{X}left(t_{1}, t_{2}right)=R_{X}left(t_{1}, t_{2}right)-m_{X}left(t_{1}right) m_{X}left(t_{2}right) CX(t1,t2)=RX(t1,t2)−mX(t1)mX(t2)
互相关函数
R X Y ( t 1 , t 2 ) = E [ X ( t 1 ) Y ( t 2 ) ] = ∫ − ∞ ∞ ∫ − ∞ ∞ x y f X Y ( x , y ; t 1 , t 2 ) d x d y R_{X Y}left(t_{1}, t_{2}right)=Eleft[Xleft(t_{1}right) Yleft(t_{2}right)right]=int_{-infty}^{infty} int_{-infty}^{infty} x y f_{X Y}left(x, y ; t_{1}, t_{2}right) mathrm{d} x mathrm{~d} y RXY(t1,t2)=E[X(t1)Y(t2)]=∫−∞∞∫−∞∞xyfXY(x,y;t1,t2)dx dy
互协方差函数
C X Y ( t 1 , t 2 ) = E [ { X ( t 1 ) − m X ( t 1 ) } { Y ( t 2 ) − m Y ( t 2 ) } ] = ∫ − ∞ ∞ ∫ − ∞ ∞ [ x − m X ( t 1 ) ] [ y − m Y ( t 2 ) ] f X Y ( x , y ; t 1 , t 2 ) d x d y begin{aligned} C_{X Y}left(t_{1}, t_{2}right) &=Eleft[left{Xleft(t_{1}right)-m_{X}left(t_{1}right)right}left{Yleft(t_{2}right)-m_{Y}left(t_{2}right)right}right] \ &=int_{-infty}^{infty} int_{-infty}^{infty}left[x-m_{X}left(t_{1}right)right]left[y-m_{Y}left(t_{2}right)right] f_{X Y}left(x, y ; t_{1}, t_{2}right) mathrm{d} x mathrm{~d} y end{aligned} CXY(t1,t2)=E[{X(t1)−mX(t1)}{Y(t2)−mY(t2)}]=∫−∞∞∫−∞∞[x−mX(t1)][y−mY(t2)]fXY(x,y;t1,t2)dx dy
两个概念交叉使用,二者只是相差一个统计平均值: C X Y ( t 1 , t 2 ) = R X Y ( t 1 , t 2 ) − m X ( t 1 ) m Y ( t 2 ) C_{X Y}left(t_{1}, t_{2}right)=R_{X Y}left(t_{1}, t_{2}right)-m_{X}left(t_{1}right) m_{Y}left(t_{2}right) CXY(t1,t2)=RXY(t1,t2)−mX(t1)mY(t2)
特征函数
Φ ( ω , t ) = E { e j ω x ( t ) } = ∫ − ∞ ∞ e j ω x f ( x , t ) d x Phi(omega, t)=Eleft{e^{j omega mathbf{x}(t)}right}=int_{-infty}^{infty} e^{j omega x} f(x, t) mathrm{d} x Φ(ω,t)=E{ejωx(t)}=∫−∞∞ejωxf(x,t)dx
平稳随机过程和序列
简单的说:统计特性不随时间变化
严格平稳(Strict Sense Stationary, SSS)
如果 x ( t ) mathbf{x}(t) x(t)时间原点的移动不改变随机过程统计性质,则我们称 x ( t ) mathbf{x}(t) x(t)是严格平稳的随机过程。在任何时刻上或任何时间区间计算严平稳过程的统计结果都是相同的。
- 严平稳过程 x ( t ) mathbf{x}(t) x(t)的一维概率密度与时间无关。
- 严平稳过程 x ( t ) mathbf{x}(t) x(t)的二维概率密度只与两个时刻 t 1 t_{1} t1和 t 2 t_{2} t2的间隔有关,与时间起点无关。
广义平稳(宽平稳)(Wide Sense Stationary, WSS)
如果
- E { x ( t ) } = η E{mathbf{x}(t)}=eta E{x(t)}=η(随机过程 x ( t ) mathbf{x}(t) x(t)的均值为常数)
- R ( t 1 , t 2 ) = R ( τ ) Rleft(t_{1}, t_{2}right)=R(tau) R(t1,t2)=R(τ)(相关函数的仅取决于 τ = t 1 − t 2 tau=t_{1}-t_{2} τ=t1−t2)
- R ( 0 ) < ∞ R(0)<infty R(0)<∞(一般忽略这一条)
则称 x ( t ) mathbf{x}(t) x(t)为广义平稳过程。
平稳随机过程的相关性分析
自相关函数
实平稳过程X(t)的自相关函数是偶函数 R X ( τ ) = R X ( − τ ) R_{X}(tau)=R_{X}(-tau) RX(τ)=RX(−τ) C X ( τ ) = C X ( − τ ) C_{X}(tau)=C_{X}(-tau) CX(τ)=CX(−τ)
平稳过程X(t) 自相关函数的最大点在,=0 处,即 ∣ R X ( τ ) ∣ ⩽ R X ( 0 ) left|R_{X}(tau)right| leqslant R_{X}(0) ∣RX(τ)∣⩽RX(0) ∣ C X ( τ ) ∣ ⩽ C X ( 0 ) left|C_{X}(tau)right| leqslant C_{X}(0) ∣CX(τ)∣⩽CX(0)
周期平稳过程X(t) 的自相关函数是周期函数,且与周期平稳过程的周期相同。 R X ( τ + T ) = R X ( τ ) R_{X}(tau+T)=R_{X}(tau) RX(τ+T)=RX(τ)
非周期平稳过程X(t) 的自相关函数满足
lim
∣
τ
∣
→
∞
R
X
(
τ
)
=
R
X
(
∞
)
=
m
X
2
lim _{|tau| rightarrow infty} R_{X}(tau)=R_{X}(infty)=m_{X}^{2}
lim∣τ∣→∞RX(τ)=RX(∞)=mX2
σ
X
2
=
R
X
(
0
)
−
R
X
(
∞
)
sigma_{X}^{2}=R_{X}(0)-R_{X}(infty)
σX2=RX(0)−RX(∞)
相关系数
相关系数是自相关函数对数学期望和方差归一化的结果,不受数学期望和方差的影响。因此相关系数可直观地说明两个随机过程的相关程度的强弱,或随机过程起伏的快慢。
r X ( τ ) = C X ( τ ) σ X 2 = R X ( τ ) − m X 2 σ X 2 r_{X}(tau)=frac{C_{X}(tau)}{sigma_{X}^{2}}=frac{R_{X}(tau)-m_{X}^{2}}{sigma_{X}^{2}} rX(τ)=σX2CX(τ)=σX2RX(τ)−mX2
相关时间
数学上:若 τ 0 tau_{0} τ0是 X ( t ) X(t) X(t)的相关时间,则认为随机过程时间间隔大于 τ 0 tau_{0} τ0的两个时刻的取值是不相关的。
工程上:1、满足 ∣ r ( τ 0 ) ∣ = 0.05 left|rleft(tau_{0}right)right|=0.05 ∣r(τ0)∣=0.05 的 τ 0 tau_{0} τ0 2、满足 τ 0 = ∫ 0 ∞ r ( τ ) d τ tau_{0}=int_{0}^{infty} r(tau) mathrm{d} tau τ0=∫0∞r(τ)dτ 的 τ 0 tau_{0} τ0
互相关函数
一般情况下,互相关函数是非奇非偶函数,即
R X Y ( τ ) = R Y X ( − τ ) R_{X Y}(tau)=R_{Y X}(-tau) RXY(τ)=RYX(−τ)
C X Y ( τ ) = C Y X ( − τ ) C_{X Y}(tau)=C_{Y X}(-tau) CXY(τ)=CYX(−τ)
互相关函数的幅度平方满足
∣ R x y ( τ ) ∣ 2 ≤ R x ( 0 ) R y ( 0 ) left|R_{x y}(tau)right|^{2} leq R_{x}(0) R_{y}(0) ∣Rxy(τ)∣2≤Rx(0)Ry(0)
互相关函数和互协方差函数的幅度满足
∣ R x y ( τ ) ∣ ≤ 1 2 [ R x ( 0 ) + R y ( 0 ) ] left|R_{x y}(tau)right| leq frac{1}{2}left[R_{x}(0)+R_{y}(0)right] ∣Rxy(τ)∣≤21[Rx(0)+Ry(0)]
联合平稳(Joint Stationary)
Two stochastic processes { X t } left{X_{t}right} {Xt} and { Y t } left{Y_{t}right} {Yt} are called jointly strict-sense stationary if their joint cumulative distribution F X Y ( x t 1 , … , x t m , y t 1 ′ , … , y t n ′ ) F_{X Y}left(x_{t_{1}}, ldots, x_{t_{m}}, y_{t_{1}^{prime}}, ldots, y_{t_{n}^{prime}}right) FXY(xt1,…,xtm,yt1′,…,ytn′) remains unchanged under time shifts.
F X Y ( x t 1 , … , x t m , y t 1 ′ , … , y t n ′ ) = F X Y ( x t 1 + τ , … , x t m + τ , y t 1 ′ + τ , … , y t n + τ ′ ) F_{X Y}left(x_{t_{1}}, ldots, x_{t_{m}}, y_{t_{1}^{prime}}, ldots, y_{t_{n}^{prime}}right)=F_{X Y}left(x_{t_{1}+tau}, ldots, x_{t_{m}+tau}, y_{t_{1}^{prime}+tau}, ldots, y_{t_{n}+tau}^{prime}right) quad FXY(xt1,…,xtm,yt1′,…,ytn′)=FXY(xt1+τ,…,xtm+τ,yt1′+τ,…,ytn+τ′) for all τ , t 1 , … , t m , t 1 ′ , … , t n ′ ∈ R tau, t_{1}, ldots, t_{m}, t_{1}^{prime}, ldots, t_{n}^{prime} in mathbb{R} τ,t1,…,tm,t1′,…,tn′∈R and for all m , n ∈ N m, n in mathbb{N} m,n∈N
如果对于任何
c
c
c,两个过程
x
(
t
)
x(t)
x(t)和
y
(
t
)
y(t)
y(t)的联合统计性质与
x
(
t
+
c
)
x(t+c)
x(t+c)和
y
(
t
+
c
)
y(t+c)
y(t+c)的联合统计性质相同,则称
x
(
t
)
x(t)
x(t)和
y
(
t
)
y(t)
y(t)是联合平稳的。
如果过程
x
(
t
)
x(t)
x(t)和
y
(
t
)
y(t)
y(t)是联合平稳的,则复过程
z
(
t
)
=
x
(
t
)
+
j
y
(
t
)
z(t) = x(t) + jy(t)
z(t)=x(t)+jy(t)也是平稳的。
联合广义平稳(联合宽平稳)
Two stochastic processes
{
X
t
}
left{X_{t}right}
{Xt} and
{
Y
t
}
left{Y_{t}right}
{Yt} are called jointly wide-sense stationary if they are both wide-sense stationary and their cross-covariance function
K
X
Y
(
t
1
,
t
2
)
=
E
[
(
X
t
1
−
m
X
(
t
1
)
)
(
Y
t
2
−
m
Y
(
t
2
)
)
]
K_{X Y}left(t_{1}, t_{2}right)=mathrm{E}left[left(X_{t_{1}}-m_{X}left(t_{1}right)right)left(Y_{t_{2}}-m_{Y}left(t_{2}right)right)right]
KXY(t1,t2)=E[(Xt1−mX(t1))(Yt2−mY(t2))] depends only on the time difference
τ
=
t
1
−
t
2
tau=t_{1}-t_{2}
τ=t1−t2. This may be summarized as follows:
m
X
(
t
)
=
m
X
(
t
+
τ
)
for all
τ
∈
R
m
Y
(
t
)
=
m
Y
(
t
+
τ
)
for all
τ
∈
R
K
X
X
(
t
1
,
t
2
)
=
K
X
X
(
t
1
−
t
2
,
0
)
for all
t
1
,
t
2
∈
R
K
Y
Y
(
t
1
,
t
2
)
=
K
Y
Y
(
t
1
−
t
2
,
0
)
for all
t
1
,
t
2
∈
R
K
X
Y
(
t
1
,
t
2
)
=
K
X
Y
(
t
1
−
t
2
,
0
)
for all
t
1
,
t
2
∈
R
begin{array}{ll} m_{X}(t)=m_{X}(t+tau) & text { for all } tau in mathbb{R} \ m_{Y}(t)=m_{Y}(t+tau) & text { for all } tau in mathbb{R} \ K_{X X}left(t_{1}, t_{2}right)=K_{X X}left(t_{1}-t_{2}, 0right) & text { for all } t_{1}, t_{2} in mathbb{R} \ K_{Y Y}left(t_{1}, t_{2}right)=K_{Y Y}left(t_{1}-t_{2}, 0right) & text { for all } t_{1}, t_{2} in mathbb{R} \ K_{X Y}left(t_{1}, t_{2}right)=K_{X Y}left(t_{1}-t_{2}, 0right) & text { for all } t_{1}, t_{2} in mathbb{R} end{array}
mX(t)=mX(t+τ)mY(t)=mY(t+τ)KXX(t1,t2)=KXX(t1−t2,0)KYY(t1,t2)=KYY(t1−t2,0)KXY(t1,t2)=KXY(t1−t2,0) for all τ∈R for all τ∈R for all t1,t2∈R for all t1,t2∈R for all t1,t2∈R
严格循环平稳
一个随机过程为 x ( t ) x(t) x(t) ,如果当原点移动 T T T的整数倍时,它的的统计特性保持不变,则称过程 x ( t ) x(t) x(t)是严格循环平稳的(SSCS) ,循环周期为 T T T 。
广义循环平稳
若对于任意整数m ,有
η
(
t
+
m
T
)
=
η
(
t
)
R
(
t
1
+
m
T
,
t
2
+
m
T
)
=
R
(
t
1
,
t
2
)
eta(t+m T)=eta(t) quad Rleft(t_{1}+m T, t_{2}+m Tright)=Rleft(t_{1}, t_{2}right)
η(t+mT)=η(t)R(t1+mT,t2+mT)=R(t1,t2)
我们就称x(t) 是广义循环平稳的(WSCS) 。
各态历经过程和序列
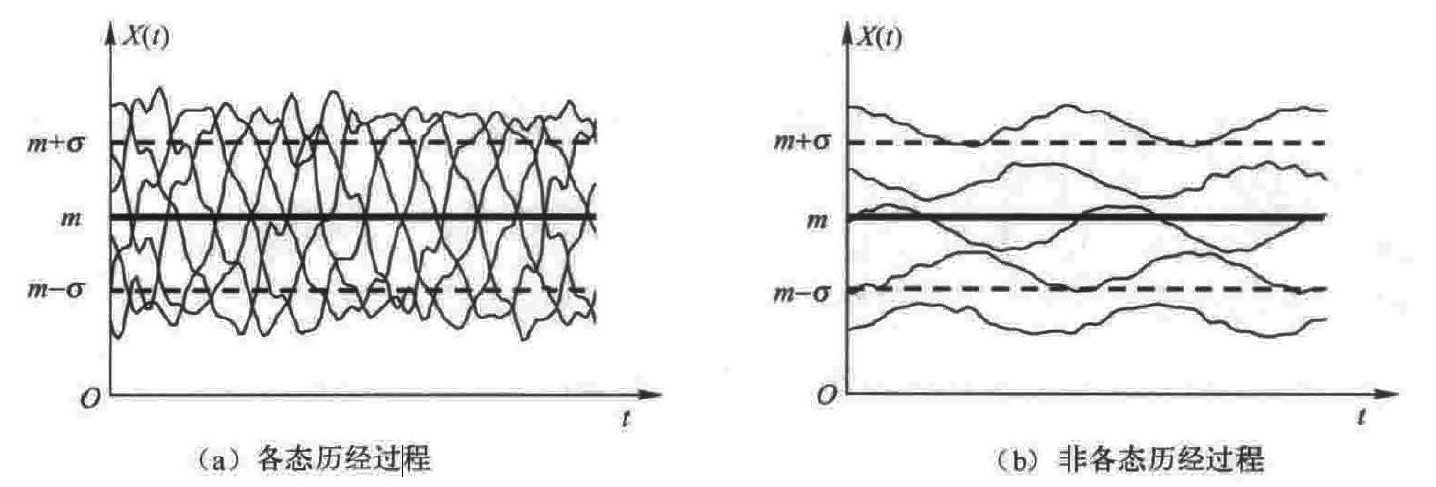
辛钦证明:在具备一定的补充条件下,对平稳过程的一个样本函数取时间均值,若观察的时间充分长,则将从概率意义上趋近它的统计均值。
例如要得出一个城市A、B两座公园哪一个更受欢迎,有两种办法。第一种办法是在一定的时间段考察两个公园(在空间上考察)的人数,人数多的为更受欢迎公园;第二种办法,随机选择一名市民,跟踪足够长的时间(在时间上考察)来统计他去两个公园的次数,去得多的为更受欢迎公园。如果这个两个结果始终一致,则表现为遍历性。
各态历经过程matlab仿真
各态历经过程的每个样本都经历了随机过程的各种可能状态,任何一个样本都能充分地代表随机过程的统计特性。
证明各态历经性:
1、时间均值等于统计均值
2、统计自相关函数等于时间自相关函数
X ( t ) ‾ = m X overline{X(t)}=m_{X} X(t)=mX
X ( t ) X ( t + τ ) ‾ = R X ( τ ) overline{X(t) X(t+tau)}=R_{X}(tau) X(t)X(t+τ)=RX(τ)
另:各种平稳过程的统计特性
| 一般随机过程 | 平稳过程 | 各态历经过程 | |
|---|---|---|---|
| 统计均值 | m X ( t ) m_{X}(t) mX(t)为时间函数 | m X m_{X} mX为常数 | m X m_{X} mX为常数 |
| 自相关函数 | R X ( t , t + τ ) R_{X}(t,t+tau) RX(t,t+τ)为二维函数 | R X ( τ ) R_{X}(tau) RX(τ)为一维函数 | R X ( τ ) R_{X}(tau) RX(τ)为一维函数 |
| 时间均值 | X ( t ) ‾ overline{X(t)} X(t)为随机变量 | X ( t ) ‾ overline{X(t)} X(t)为随机变量 | X ( t ) ‾ overline{X(t)} X(t)为常数 |
| 时间自相关函数 | X ( t ) X ( t + τ ) ‾ overline{X(t) X(t+tau)} X(t)X(t+τ)为随机过程 | X ( t ) X ( t + τ ) ‾ overline{X(t) X(t+tau)} X(t)X(t+τ)为随机过程为随机过程 | X ( t ) X ( t + τ ) ‾ overline{X(t) X(t+tau)} X(t)X(t+τ)为随机过程为确定时间函数 |
收敛
逐点收敛有很大的局限性,实际上很难满足,应用受到了限制。因此人们寻求较弱意义下的收敛。一般应用的收敛有以概率1收敛、均方收敛、依概率收敛和分布收敛等。
各个收敛的定义有强弱之分。强收敛可以推出弱收敛。
以概率1收敛
属千很强的收敛条件,又称为几乎处处收敛,其定义接近于函数逐点收敛的定义。
P
(
lim
n
→
∞
X
n
=
x
)
=
1
则
X
n
→
a.s.
x
Pleft(lim _{n rightarrow infty} X_{n}=xright)=1text { 则 } X_{n} stackrel{text { a.s. }}{rightarrow} x
P(n→∞limXn=x)=1 则 Xn→ a.s. x
依概率收敛
和依概率1收敛的定义有相似之处,但本质上,依概率1收敛是比依概率收敛更“强”的收敛性质。
lim
n
→
∞
P
(
∣
X
n
−
X
∣
⩾
ε
)
=
0
则
X
n
→
P
X
lim _{n rightarrow infty} Pleft(left|X_{n}-Xright| geqslant varepsilonright)=0text{ 则 }X_{n} stackrel{P}{rightarrow} X
n→∞limP(∣Xn−X∣⩾ε)=0 则 Xn→PX
依分布收敛
依分布收敛是最宽松的收敛方式之一。这种收敛不要求查看每个$omega $,只要求序列的分布趋向于某个极限。
lim
n
→
∞
p
(
X
n
⩽
x
)
=
P
(
X
⩽
x
)
则
X
n
→
d
X
lim _{n rightarrow infty} pleft(X_{n} leqslant xright)=P(X leqslant x) text { 则 }X_{n} stackrel{d}{rightarrow} X
n→∞limp(Xn⩽x)=P(X⩽x) 则 Xn→dX
均方收敛(Mean-Square或 m.s. 收敛)
lim n → ∞ E { ∣ x n − x ∣ 2 } = 0 则 X n → L 2 X lim _{n rightarrow infty} Eleft{left|mathbf{x}_{n}-mathbf{x}right|^{2}right}=0text { 则 }X_{n} stackrel{mathbf{L}^{2}}{rightarrow} X n→∞limE{∣xn−x∣2}=0 则 Xn→L2X
-
随机过程的连续性通常指在均方收敛意义下的连续。
-
均方连续必均值连续,对随机变量求期望就是一个很常用的处理。
证明: E [ { X ( t + Δ t ) − X ( t ) } 2 ] ⩾ E 2 [ X ( t + Δ t ) − X ( t ) ] Eleft[{X(t+Delta t)-X(t)}^{2}right] geqslant E^{2}[X(t+Delta t)-X(t)] E[{X(t+Δt)−X(t)}2]⩾E2[X(t+Δt)−X(t)]
随机过程求极限和求期望顺序可互换
随机微分(对时间)
均方可微(MS differentiable)
定义
如果过程 x ( t ) mathbf{x}(t) x(t)满足, lim Δ t → 0 E [ { X ( t + Δ t ) − X ( t ) Δ t − X ′ ( t ) } 2 ] = 0 lim _{Delta t rightarrow 0} Eleft[left{frac{X(t+Delta t)-X(t)}{Delta t}-X^{prime}(t)right}^{2}right]=0 limΔt→0E[{ΔtX(t+Δt)−X(t)−X′(t)}2]=0则称过程 x ( t ) mathbf{x}(t) x(t)是均方可微的。
定理
如果过程 x ( t ) mathbf{x}(t) x(t)的相关函数在 t 1 = t 2 t_{1}=t_{2} t1=t2时连续,且二阶混合偏导数 ∂ 2 R ( t 1 , t 2 ) ∂ t 1 ∂ t 2 ∣ t 1 = t 2 left.frac{partial^{2} Rleft(t_{1}, t_{2}right)}{partial t_{1} partial t_{2}}right|_{t_{1}=t_{2}} ∂t1∂t2∂2R(t1,t2)∣∣∣t1=t2存在,则过程 x ( t ) mathbf{x}(t) x(t)是均方可微的。
运算法则
均方导数运算和数学期望运算的次序可以交换。
结论
随机过程均方导数的自相关函数等于随机过程自相关函数的二阶偏导数。
R X ′ ( t 1 , t 2 ) = ∂ 2 R X ( t 1 , t 2 ) ∂ t 1 ∂ t 2 R_{X^{prime}}left(t_{1}, t_{2}right)=frac{partial^{2} R_{X}left(t_{1}, t_{2}right)}{partial t_{1} partial t_{2}} RX′(t1,t2)=∂t1∂t2∂2RX(t1,t2)
平稳过程导数的自相关函数等于原过程自相关函数的二阶导数的负值
R X ′ ( τ ) = R X ′ ( t , t + τ ) = − d 2 R X ( τ ) d τ 2 begin{aligned} R_{X^{prime}}(tau)=R_{X^{prime}}(t, t+tau)=-frac{mathrm{d}^{2} R_{X}(tau)}{mathrm{d} tau^{2}} end{aligned} RX′(τ)=RX′(t,t+τ)=−dτ2d2RX(τ)
平稳随机过程的导数是均值为零的平稳随机过程。
平稳随机过程与其导数过程在同一时刻的状态是两个相互正交的随机变量。
R
X
Y
(
0
)
=
d
R
X
(
τ
)
d
τ
∣
τ
=
0
=
0
R_{X Y}(0)=left.frac{mathrm{d} R_{X}(tau)}{mathrm{d} tau}right|_{tau=0}=0
RXY(0)=dτdRX(τ)∣∣∣∣τ=0=0
随机积分(对时间)
定义
把积分区间
[
a
,
b
]
[a,b]
[a,b]分成
n
n
n 个小区间
Δ
t
i
,
Delta t_{i},
Δti, 令
Δ
t
=
max
Δ
t
i
,
Delta t=max Delta t_{i},
Δt=maxΔti, 当
n
→
∞
n rightarrow infty
n→∞ 时
lim
Δ
t
→
0
E
[
{
Y
−
∑
i
=
1
n
X
(
t
i
)
Δ
t
i
}
2
]
=
0
lim _{Delta t rightarrow 0} Eleft[left{Y-sum_{i=1}^{n} Xleft(t_{i}right) Delta t_{i}right}^{2}right]=0
Δt→0limE⎣⎡{Y−i=1∑nX(ti)Δti}2⎦⎤=0
Y Y Y就定义为 X ( t ) X(t) X(t)在均方意义下的积分。
定理
如果下式成立,则
x
(
t
)
mathrm{x}(t)
x(t) 是均方可积的。
∫
a
b
∫
a
b
∣
R
(
t
1
,
t
2
)
∣
d
t
1
d
t
2
<
∞
int_{a}^{b} int_{a}^{b}left|Rleft(t_{1}, t_{2}right)right| mathrm{d} t_{1} mathrm{~d} t_{2}<infty
∫ab∫ab∣R(t1,t2)∣dt1 dt2<∞
运算法则
均方积分运算和数学期望运算的次序可以交换。
结论
对随机过程积分,若积分上限和下限中不含t则积分结果为随机变量,若积分上限和下限中含t则积分结果为随机过程。
随机过程积分为随机变量时的方差等于原过程的协方差函数的二重积分。
Y 2 = ∫ − ∞ ∞ ∫ − ∞ ∞ X ( t 1 ) X ( t 2 ) d t 1 d t 2 Y^{2}=int_{-infty}^{infty} int_{-infty}^{infty} Xleft(t_{1}right) Xleft(t_{2}right) mathrm{d} t_{1} mathrm{~d} t_{2} Y2=∫−∞∞∫−∞∞X(t1)X(t2)dt1 dt2
E [ Y 2 ] = ∫ − ∞ ∞ ∫ − ∞ ∞ E [ X ( t 1 ) X ( t 2 ) ] d t 1 d t 2 = ∫ − ∞ ∞ ∫ − ∞ ∞ R X ( t 1 t 2 ) d t 1 d t 2 Eleft[Y^{2}right]=int_{-infty}^{infty} int_{-infty}^{infty} Eleft[Xleft(t_{1}right) Xleft(t_{2}right)right] d t_{1} d t_{2}=int_{-infty}^{infty} int_{-infty}^{infty} R_{X}left(t_{1} t_{2}right) mathrm{d} t_{1} mathrm{~d} t_{2} E[Y2]=∫−∞∞∫−∞∞E[X(t1)X(t2)]dt1dt2=∫−∞∞∫−∞∞RX(t1t2)dt1 dt2
D [ Y ] = E [ Y 2 ] − E 2 [ Y ] = ∫ − ∞ ∞ ∫ − ∞ ∞ R X ( t 1 t 2 ) d t 1 d t 2 − E 2 [ ∫ − ∞ ∞ X ( t ) d t ] = ∫ − ∞ ∞ ∫ − ∞ ∞ R X ( t 1 , t 2 ) d t 1 d t 2 − ∫ − ∞ ∞ ∫ ∞ ∞ m X ( t 1 , t 2 ) d t 1 d t 2 = ∫ − ∞ ∞ ∫ − ∞ ∞ C X ( t 1 , t 2 ) d t 1 d t 2 D[Y]=Eleft[Y^{2}right]-E^{2}[Y]=int_{-infty}^{infty} int_{-infty}^{infty} R_{X}left(t_{1} t_{2}right) mathrm{d} t_{1} mathrm{~d} t_{2}-E^{2}left[int_{-infty}^{infty} X(t) mathrm{d} tright] \ =int_{-infty}^{infty} int_{-infty}^{infty} R_{X}left(t_{1}, t_{2}right) mathrm{d} t_{1} mathrm{~d} t_{2}-int_{-infty}^{infty} int_{infty}^{infty} m_{X}left(t_{1}, t_{2}right) mathrm{d} t_{1} mathrm{~d} t_{2}=int_{-infty}^{infty} int_{-infty}^{infty} C_{X}left(t_{1}, t_{2}right) mathrm{d} t_{1} mathrm{~d} t_{2} D[Y]=E[Y2]−E2[Y]=∫−∞∞∫−∞∞RX(t1t2)dt1 dt2−E2[∫−∞∞X(t)dt]=∫−∞∞∫−∞∞RX(t1,t2)dt1 dt2−∫−∞∞∫∞∞mX(t1,t2)dt1 dt2=∫−∞∞∫−∞∞CX(t1,t2)dt1 dt2
随机过程积分为随机过程时的自相关函数等于原过程自相关函数的二重积分。
如果
Y
(
t
)
=
∫
0
t
X
(
τ
)
d
τ
,
Y(t)=int_{0}^{t} X(tau) mathrm{d} tau,
Y(t)=∫0tX(τ)dτ, 它的自相关函数为
R
Y
(
t
1
,
t
2
)
=
E
[
Y
(
t
1
)
Y
(
t
2
)
]
=
E
[
∫
0
t
∫
0
t
2
X
(
τ
)
X
(
τ
′
)
d
τ
d
τ
′
]
=
∫
0
t
∫
0
t
i
R
X
(
τ
,
τ
′
)
d
τ
d
τ
′
R_{Y}left(t_{1}, t_{2}right)=Eleft[Yleft(t_{1}right) Yleft(t_{2}right)right]=Eleft[int_{0}^{t} int_{0}^{t_{2}} X(tau) Xleft(tau^{prime}right) mathrm{d} tau mathrm{d} tau^{prime}right]=int_{0}^{t} int_{0}^{t_{i}} R_{X}left(tau, tau^{prime}right) mathrm{d} tau mathrm{d} tau^{prime}
RY(t1,t2)=E[Y(t1)Y(t2)]=E[∫0t∫0t2X(τ)X(τ′)dτdτ′]=∫0t∫0tiRX(τ,τ′)dτdτ′
当
t
1
=
t
2
t_{1}=t_{2}
t1=t2 时,上式退化为随机过程
Y
(
t
)
Y(t)
Y(t) 的二阶原点矩
E
[
Y
2
(
t
)
]
=
∫
0
t
∫
0
t
R
X
(
τ
,
τ
′
)
d
τ
d
τ
′
Eleft[Y^{2}(t)right]=int_{0}^{t} int_{0}^{t} R_{X}left(tau, tau^{prime}right) mathrm{d} tau mathrm{d} tau^{prime}
E[Y2(t)]=∫0t∫0tRX(τ,τ′)dτdτ′
另:联合正态
如果随机变量
x
x
x 和
y
y
y 的联合概率密度函数为
f
(
x
,
y
)
=
A
exp
{
−
1
2
(
1
−
r
2
)
(
(
x
−
η
1
)
2
σ
1
2
−
2
r
(
x
−
η
1
)
(
y
−
η
2
)
σ
1
σ
2
+
(
y
−
η
2
)
2
σ
2
2
)
}
f(x, y)=A exp left{-frac{1}{2left(1-r^{2}right)}left(frac{left(x-eta_{1}right)^{2}}{sigma_{1}^{2}}-2 r frac{left(x-eta_{1}right)left(y-eta_{2}right)}{sigma_{1} sigma_{2}}+frac{left(y-eta_{2}right)^{2}}{sigma_{2}^{2}}right)right}
f(x,y)=Aexp{−2(1−r2)1(σ12(x−η1)2−2rσ1σ2(x−η1)(y−η2)+σ22(y−η2)2)}
我们称它们是联合正态的。这个函数
f
(
x
,
y
)
f(x, y)
f(x,y) 是恒正的,并且如果
A
=
1
2
π
σ
1
σ
2
1
−
r
2
∣
r
∣
<
1
A=frac{1}{2 pi sigma_{1} sigma_{2} sqrt{1-r^{2}}} quad|r|<1
A=2πσ1σ21−r21∣r∣<1
负二次式。我们把这个函数记作
N
(
η
1
,
η
2
,
σ
1
2
,
σ
2
2
,
r
)
Nleft(eta_{1}, eta_{2}, sigma_{1}^{2}, sigma_{2}^{2}, rright)
N(η1,η2,σ12,σ22,r)
下面我们就会看到,
η
1
eta_{1}
η1 和
η
2
eta_{2}
η2 是
x
x
x 和
y
y
y 的均值,而
σ
1
2
sigma_{1}^{2}
σ12 和
σ
2
2
sigma_{2}^{2}
σ22 是它们的方差。
r
r
r 的意义将 在后面的习题 6 - 30 中给出(相关系数)。
可以证明,
x
boldsymbol{x}
x 和
y
boldsymbol{y}
y 的边缘概率密度函数为
f
x
(
x
)
=
1
σ
1
2
π
e
−
(
x
−
η
1
)
2
/
2
σ
1
2
,
f
y
(
y
)
=
1
σ
2
2
π
e
−
(
y
−
η
2
)
2
/
2
σ
2
2
(
6
−
26
)
f_{x}(x)=frac{1}{sigma_{1} sqrt{2 pi}} mathrm{e}^{-left(x-eta_{1}right)^{2} / 2 sigma_{1}^{2}}, f_{y}(y)=frac{1}{sigma_{2} sqrt{2 pi}} mathrm{e}^{-left(y-eta_{2}right)^{2} / 2 sigma_{2}^{2}} quad(6-26)
fx(x)=σ12π1e−(x−η1)2/2σ12,fy(y)=σ22π1e−(y−η2)2/2σ22(6−26)
联合正态:若随机变量
x
boldsymbol{x}
x 和
y
y
y 是联合正态的,即服从
N
(
μ
x
,
μ
y
,
σ
x
2
,
σ
y
2
,
ρ
)
Nleft(mu_{x}, mu_{y}, sigma_{x}^{2}, sigma_{y}^{2}, rhoright)
N(μx,μy,σx2,σy2,ρ)
且
z
=
a
x
+
b
y
,
w
=
c
x
+
d
y
z=a x+b y, quad w=c x+d y
z=ax+by,w=cx+dy
类似于
f
x
y
(
x
,
y
)
,
z
f_{x y}(x, y), z
fxy(x,y),z 和
w
w
w 的概率密度函数也是指数函敕,指数部分是和的二次多项式,因此也 是联合正态的。用(
6
−
25
6-25
6−25 ) 式的概念,z和
w
w
w 服从正态分布
N
(
μ
z
,
μ
w
,
σ
x
2
,
σ
w
2
,
ρ
z
w
)
Nleft(mu_{z}, mu_{w}, sigma_{x}^{2}, sigma_{w}^{2}, rho_{z w}right)
N(μz,μw,σx2,σw2,ρzw), 通过计算知道
μ
x
=
a
μ
x
+
b
μ
y
μ
w
=
c
μ
x
+
d
μ
y
σ
z
2
=
a
2
σ
x
2
+
2
a
b
ρ
σ
x
σ
y
+
b
2
σ
y
2
σ
w
2
=
c
2
σ
x
2
+
2
c
d
ρ
σ
x
σ
y
+
d
2
σ
y
2
ρ
x
w
=
a
c
σ
x
2
+
(
a
d
+
b
c
)
ρ
σ
x
σ
y
+
b
d
σ
y
2
σ
x
σ
w
begin{array}{l} mu_{x}=a mu_{x}+b mu_{y} \ mu_{w}=c mu_{x}+d mu_{y} \ sigma_{z}^{2}=a^{2} sigma_{x}^{2}+2 a b rho sigma_{x} sigma_{y}+b^{2} sigma_{y}^{2} \ sigma_{w}^{2}=c^{2} sigma_{x}^{2}+2 c d rho sigma_{x} sigma_{y}+d^{2} sigma_{y}^{2} \ rho_{x w}=frac{a c sigma_{x}^{2}+(a d+b c) rho sigma_{x} sigma_{y}+b d sigma_{y}^{2}}{sigma_{x} sigma_{w}} end{array}
μx=aμx+bμyμw=cμx+dμyσz2=a2σx2+2abρσxσy+b2σy2σw2=c2σx2+2cdρσxσy+d2σy2ρxw=σxσwacσx2+(ad+bc)ρσxσy+bdσy2
特别是,任意两个联合正态的随机变量的线性组合仍然是正态的。
如果两个随机变量是联合正态的,则它们也是边缘正态的。但反之并不成立。
联合正态可定义如下: 如果对任意 a a a 与 b b b, 其和 a x + b y a x+b y ax+by 是正态的,则 x x x 与 y y y 就是联合正态的。
高斯随机过程
宽平稳⾼斯过程⼀定是严平稳过程。(高斯过程三阶以上的中心矩为零)这条性质表明了高斯过程独有的特性,严平稳可是很难达到的!
若平稳⾼斯过程在任意两个不同时刻 t1和 t2 是不相关的,那么也一定是互相独立的。( E { x y } = E { x } E { y } E{mathbf{x y}}=E{mathbf{x}} E{mathbf{y}} E{xy}=E{x}E{y}等价于)
平稳高斯过程与确定时间信号之和也是高斯过程。这点可以理解为高斯过程搭载在另一个信号上,高斯过程提供了随机性。若该确定时间信号是时变的,则会破坏和信号的平稳性。
如果高斯过程的积分存在,它也将是高斯分布的随机变量或随机过程。
平稳高斯过程导数的一维概率密度也是高斯分布的,其数学期望为零,方差为
σ
2
∣
r
′
′
(
0
)
∣
sigma^{2}left|r^{prime prime}(0)right|
σ2∣r′′(0)∣, 即
f
X
′
(
x
′
)
=
1
2
π
σ
2
∣
r
′
′
(
0
)
∣
exp
[
−
x
′
2
2
σ
2
∣
r
′
′
(
0
)
∣
]
f_{X^{prime}}left(x^{prime}right)=frac{1}{sqrt{2 pi sigma^{2}left|r^{prime prime}(0)right|}} exp left[-frac{x^{prime 2}}{2 sigma^{2}left|r^{prime prime}(0)right|}right]
fX′(x′)=2πσ2∣r′′(0)∣1exp[−2σ2∣r′′(0)∣x′2]
平稳高斯过程导数的 二维概率密度是高斯分布的,平稳高斯过程与其导数的联合概率密度也是高斯分布的 。
白噪声
将具有均匀分布的噪声称为均匀噪声,量化噪声就是均匀噪声。从功率谱的角度看,如果一个随机过程的功率谱密度是常数,则无论它是什么分布,都称它为白噪声。
在误差分析时经常遇到均匀分布,如数字信号中的量化噪声。由于 A / D mathrm{A} / mathrm{D} A/D 转换器的字长有限,模拟信号通过 A/D 转换时,势必要舍弃部分信息。丢失信息后相当于使信号附加了一部 分噪声,称为量化噪声。量化噪声分为截尾噪声和舍入噪声,它们都是均匀分布的,且方差 相同,不同的是分布的区间。若量化的最小单位是 ε varepsilon ε ,舍入噪声在 [ − ε / 2 , ε / 2 ] [-varepsilon / 2, varepsilon / 2] [−ε/2,ε/2] 内均匀分布, 数学期望为零; 而截尾噪声在 [ − ε , 0 ] [-varepsilon, 0] [−ε,0] 内均匀分布,因此数学期望为 − ε / 2 -varepsilon / 2 −ε/2 。
最后
以上就是热心便当最近收集整理的关于随机过程知识总结的全部内容,更多相关随机过程知识总结内容请搜索靠谱客的其他文章。








发表评论 取消回复