第一章 矩阵与线性方程组 （二）

一、 矩阵的基本运算

1. 复矩阵和实矩阵

令R表示实数集合，C表示复数集合。
一个复矩阵定义为按照长方阵列排列的复数集合，记作

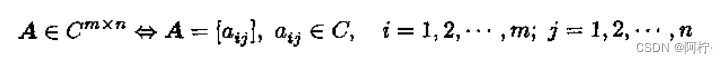
类似地，一个实矩阵记作

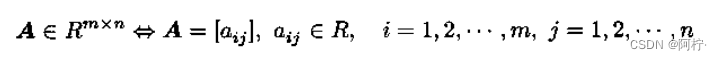
2. 转置、复数共轭

• 若$A=[a_{ij}]$是一个m * n矩阵，则$A$的转置记作$A^T$,是一个n * m矩阵，定义为$[A^T{]}_{ij}=a_{ji}$
• 矩阵$A$的复数共轭$A^{\ast }$定义为$[A^{\ast }{]}_{ij}=a_{ij}^{\ast }$
• 复共轭转置记作$A^H$，定义为
  
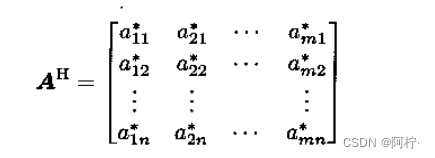
  共轭转置又叫Hermitian伴随、Hermitian转置或Hermitian共轭。满足$A^H=A$的正方复矩阵称为Hermitian矩阵或共轭对称矩阵。

共轭转置与转置之间存在下列关系：
$$A^H=(A^{\ast }{)}^T=(A^T{)}^{\ast }$$

3. 简单的代数运算

3.1 两个矩阵的加法

两个m * n矩阵$A=[a_{ij}]$ 和 $B=[b_{ij}]$之和记作$A+B$， 定义为$[A+B{]}_{ij}=a_{ij}+b_{ij}$

3.2 矩阵与一个标量的乘法

令$A=[a_{ij}]$是一个m * n矩阵，且$\alpha$是一个标量。乘积$\alpha$$A$是一个m * n矩阵，定义为$[$ $\alpha$$A{]}_{ij}=\alpha a_{ij}$

3.3 矩阵与向量的乘积

m * n矩阵$A=[a_{ij}]$ 与r * 1 向量$x=[x_1,x_2,\cdot \cdot \cdot ,x_r{]}^T$的乘积$Ax$只有当n=r时才存在，它是一个m * 1向量，定义为

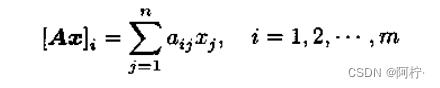
3.4 矩阵与矩阵的乘积

m * n矩阵$A=[a_{ij}]$ 与r * s 矩阵$B=[b_{ij}]$的乘积$AB$只有当n=r时才存在，它是一个m * s向量，定义为

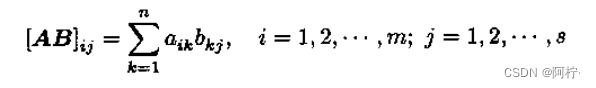
4. 运算规则

4.1 加法

• 加法交换律：$A+B=B+A$
• 加法结合律：$(A+B)+C=A+(B+C)$

4.2 乘法

• 乘法结合律：$A(BC)=(AB)C$
• 乘法左分配律：若$A$和$B$是两个m * n矩阵，且$C$是一个n * p矩阵，则$(A+B)C=AC+BC$
• 乘法右分配律：若$A$是两个m * n矩阵，且$B$和$C$是一个n * p矩阵，则$A(B+C)=AB+AC$
• 若$\alpha$是一个标量，并且$A$和$B$是两个m* n矩阵，则$\alpha$ $(A+B)=\alpha A+\alpha B$

5. 逆矩阵

令A是一个n * n矩阵。称矩阵$A$可逆，若可以找到一个n * n矩阵$A^{-1}$ 满足$A{A}^{-1}=A^{-1}A=I$，并称$A^{-1}$是矩阵$A$的逆矩阵。

6. 矩阵的共轭、转置、共轭转置和逆矩阵的性质

6.1 矩阵的共轭、转置和共轭转置满足分配律

$(A+B{)}^{\ast }=A^{\ast }+B^{\ast }$
$(A+B{)}^T=A^T+B^T$
$(A+B{)}^H=A^H+B^H$

6.2 矩阵乘积的转置、共轭转置和逆矩阵满足关系式

$(AB{)}^T=B^T{A}^T$
$(AB{)}^H=B^H{A}^H$
$(AB{)}^{-1}=B^{-1}{A}^{-1}$ A,B为可逆的正方矩阵

6.3 共轭、转置和共轭转置等符号均可与求逆符号交换

$(A^{\ast }{)}^{-1}=(A^{-1}{)}^{\ast }$ , $(A^T{)}^{-1}=(A^{-1}{)}^T$,$(A^H{)}^{-1}=(A^{-1}{)}^H$
因此，常常分别采用紧凑的数学符号$A^{-\ast }$,$A^{-T}$,$A^{-H}$

6.4 对应任意矩阵$A$，矩阵$B=A^{H}A$都是Hermitian矩阵

若$A$可逆，则对于Hermitian矩阵$B=A^{H}A$，有$A^{-H}B{A}^{-1}=A^{-H}{A}^{H}A{A}^{-1}=I$

最后

以上就是自由发箍为你收集整理的矩阵分析与应用+张贤达第一章 矩阵与线性方程组 （二）一、 矩阵的基本运算的全部内容，希望文章能够帮你解决矩阵分析与应用+张贤达第一章 矩阵与线性方程组 （二）一、 矩阵的基本运算所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。