1 写在前面

当我们试图用公式规律去描述真实事物时，总会有有很多不确定的因素，这些因素往往会对描述结果产生干扰。但是我们又想对不确定下的运动进行精细的数学描述，建立在可测概率空间上的随机过程便应运而生。

这篇文章的目的是浅层分解随机过程，串联几个重要的概念，说明随机过程中最简单的一条路径。

1.1 符号说明

$\Omega$, sample space, 样本空间 Ω = { ω 1 , ω 2 , . . . } Omega = {omega_1, omega_2, ...} Ω={ω1​,ω2​,...}

$\omega$, sample point / observation : $\omega \in \Omega$

$\mathcal{F}$, omega-field, 集合族/事件域（可测时）

$\Psi$：an event, a subset of outcomes. $\Psi \subset \Omega ,\Psi \in \mathcal{F}$

$(\Omega ,\mathcal{F})$, measurable space, 可测空间

$P$, Possibility: 可测空间$(\Omega ,\mathcal{F})$上的概率

$X$, random variables (RV): 定义在 $\Omega$ 上取值于实数集 $\mathbb{R}$ 的函数，当 ∀ x ∈ R , { ω : X ( ω ) ≤ x } ∈ F forall x in mathbb{R}, {omega: X(omega) leq x} in mathscr{F} ∀x∈R,{ω:X(ω)≤x}∈F 时，则 $X$ 为 $\mathcal{F}$ 上的随机变量（包括连续与离散）。

$T$, 指标集/参数集

$S$, 状态空间：$X(t)$ 所有可能状态的集合

$cdf(cumulativedistributionfunction)$, 累计分布函数：$F(x)=\mathbb{P}(X\le x)$

$pdf(probabilitydensityfunction)$, 概率密度函数 $p(x)$（对于连续 $cdfF(x)$）：$F(x)={\int }_{-\infty }^{x}p(u)du$

1.2 基本概念

• 随机过程：概率空间 $(\Omega ,\mathcal{F},P)$上的一族随机变量 { X ( t ) , t ∈ T } {X(t), tin T} {X(t),t∈T}

• Kolmogorov theorem: 设分布函数族 { F t 1 , t 2 , . . . , t n ( x 1 , x 2 , . . . , x n ) , t 1 , t 2 , . . . , t n ∈ T , n ≥ 1 } {F_{t_1,t_2,..., t_n}(x_1, x_2,...,x_n), t_1,t_2,..., t_n in T, ngeq1} {Ft1​,t2​,...,tn​​(x1​,x2​,...,xn​),t1​,t2​,...,tn​∈T,n≥1} 满足对称性和相容性，则必存在一个随机过程 { X ( t ) , t ∈ T } {X(t), tin T} {X(t),t∈T} ，使分布函数族 { F t 1 , t 2 , . . . , t n ( x 1 , x 2 , . . . , x n ) , t 1 , t 2 , . . . , t n ∈ T , n ≥ 1 } {F_{t_1,t_2,..., t_n}(x_1, x_2,...,x_n), t_1,t_2,..., t_n in T, ngeq1} {Ft1​,t2​,...,tn​​(x1​,x2​,...,xn​),t1​,t2​,...,tn​∈T,n≥1} 恰好是 { X ( t ) , t ∈ T } {X(t), tin T} {X(t),t∈T} 的有限维分布族。

• Markov Property，马尔可夫性质：若一个随机过程未来状态的条件概率分布仅依赖于当前状态，那这个随机过程具备马尔科夫性，又称马尔可夫过程（Markov Process）。常见 Markov Process 有：独立随机过程，独立增量过程，泊松过程，维纳过程，Markov Chain, Brownian Motion

• Martingale Property，鞅性质：鞅是一组随机变量的序列，给定了前0~(i-1)个变量，预测第(i+1)个变量的值，该值的均值就是该序列的最后一个值。

2 随机过程的拆解与刻画

确定性过程研究一个量随时间确定的变化，而随机过程描述的是一个量随时间可能的变化。回归现实生活中可以将随机过程 { X ( t ) , t ∈ T } {X(t), tin T} {X(t),t∈T} 理解为物理、自然或是社会的系统，$X(t)$ 就表示 $t$ 时刻这个系统所处的状态，而这个状态上基于概率的不确定概率。

除了从定义角度理解之外，还可以将随机过程看作为 $T\times \Omega$ 上的二元函数 { X ( t , ω ) , t ∈ T , ω ∈ Ω } {X(t,omega), tin T, omega in Omega } {X(t,ω),t∈T,ω∈Ω}。当样本点 $\omega$ 固定时， $X(t,\omega )$ 是定义在 $T$ 上的函数，相当于随机过程的一个样本函数；当固定时刻 $t$ 时， $X(t_0)=X(t,\omega )$ 是概率空间 $(\Omega ,\mathcal{F},P)$上的一个随机变量。

2.1 有限维分布 —— 完整地刻画随机过程

顺着二元函数的思路，capture 一个随机过程便可以从刻画各个时刻 $t$ 下随机变量 $X(t)$ 的概率分布 F ( x , t ) = P { X ( t ) ≤ x } F(x,t) = P{X(t) leq x} F(x,t)=P{X(t)≤x} 入手：
各时点下的 RV 分布 $F(x,t)$ 为随机过程 { X ( t ) , t ∈ T } {X(t), tin T} {X(t),t∈T} 的一维分布。

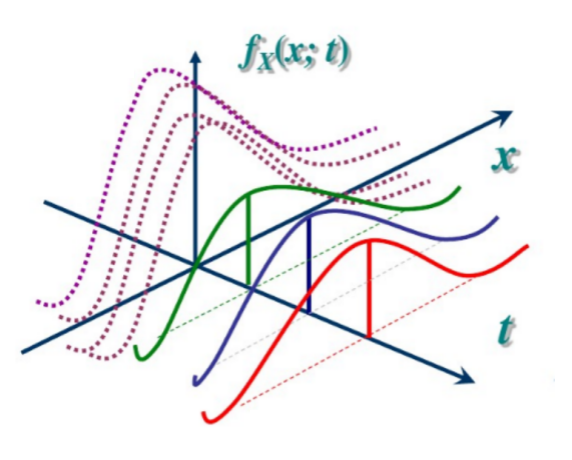
从固定时点的一个 $RV$ 到随机过程所包含的 $n$ 个 $RV$，就涉及到联合分布问题。随机过程在两个不同时刻下的分布表示为 F t 1 , t 2 ( x 1 , x 2 ) = P { X ( t 1 ) ≤ x 1 , X ( t 2 ) ≤ x 2 } F_{t_1,t_2}(x_1, x_2)=P{X(t_1)leq x_1, X(t_2)leq x_2} Ft1​,t2​​(x1​,x2​)=P{X(t1​)≤x1​,X(t2​)≤x2​}，称为二维分布，同理有随机过程的三维分布、$n$ 维分布等。随机过程的所有一维分布（$C_n^1$个）、二维分布（$C_n^2$个）、…、n 维分布（$C_n^n$个）等全体分布称为随机过程的的有限分布族，也可以理解为事件域 $\mathcal{F}$ 中所有事件的分布函数。

掌握了随机过程的有限分布族，就知道了随机过程中任意数量 $RV$ 之间的联合分布以及相依关系，又根据 Kolmogorov 定理，掌握随机过程的有限分布族就等于完整的掌握了这个随机过程。

Kolmogorov 定理的意义在于：论证了有限维分布族能够完整的描述随机过程。

2.2 数字特征 —— 刻画随机过程的关键性质

看有限分布族的面相可知，有限分布族并不“有限”，想知悉这一串花式分布是一件非常困难的事。所以在实际中，会用一些特殊性质来代替大量分布函数来描述随机过程，如：均值函数（expectation function）、二阶矩函数（second moments function, including Var, covariance and etc.）等。

• expectation function: ${\mu }_{X(t)}=E[X(t)]$
• variance function: $Var[X(t)]=E[(X(t_1)-{\mu }_{X(t_1)}{)}^2]=\gamma (t,t)$
• covariance functions: γ ( t 1 , t 2 ) = E { [ X ( t 1 ) − μ X ( t 1 ) ] [ X ( t 2 ) − μ X ( t 2 ) ] } ( s , t ∈ T ) gamma(t_1,t_2) = E{[X(t_1)-mu_{X(t_1)}][X(t_2)-mu_{X(t_2)}]}(s,t in T) γ(t1​,t2​)=E{[X(t1​)−μX(t1​)​][X(t2​)−μX(t2​)​]}(s,t∈T)
  协方差函数可以理解为时刻 $t_1$ 上随机变量 $X(t_1)$ 和时刻 $t_2$ 上随机变量 $X(t_2)$ 的波动乘积的期望。如果二者此消彼长，则 $\gamma (t_1,t_2)$ 为负；荣辱与共则 $\gamma (t_1,t_2)$ 为正；无关则 $\gamma (t_1,t_2)$ 为 0（极端情况$X(t_1)$为常数，不受任何其他$X(t)$变化影响，因为$X(t_1)-{\mu }_{X(t_1)}$恒为 0 所以协方差为 0）
  对于 $n$ 个 $RV$，任意两个 $RV$ 能得出一个 covariance，所有 covariance 构成 covariance matrix $\Sigma$：

$\Sigma =\left[\begin{array}{cccc}\gamma (t_1,t_1)& \gamma (t_1,t_2)& ...& \gamma (t_1,t_n)\\ \gamma (t_2,t_1)& \gamma (t_2,t_2)& ...& \gamma (t_2,t_n)\\ ...& ...& ...& ...\\ \gamma (t_n,t_1)& \gamma (t_n,t_2)& ...& \gamma (t_n,t_n)\end{array}\right]$

• Correlation function: $\rho (s,t)=\frac{\gamma (s,t)}{\sigma x\sigma y}$
  相关函数可以理解为去量纲后特殊的协方差函数，有一致的限制范围 [-1, 1]，更有利于展示两个 $RV$ 间的相关程度。

In the stochastic process of financial risk, the second moments often do not exist

最后

以上就是魁梧黄蜂为你收集整理的随机过程笔记（一）：基本概念梳理1 写在前面2 随机过程的拆解与刻画的全部内容，希望文章能够帮你解决随机过程笔记（一）：基本概念梳理1 写在前面2 随机过程的拆解与刻画所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。