平稳过程与一些非平稳过程

平稳过程

常用的概念是宽平稳过程（WSS），宽平稳过程要求该过程的一阶矩和二阶矩不时变，即:

E { x ( t ) } = m x ( t ) = m x ( t + τ ) ∀ τ ∈ R mathbb{E}{x(t)}=m_{x}(t)=m_{x}(t+tau) forall tau in mathbb{R} E{x(t)}=mx​(t)=mx​(t+τ)∀τ∈R

E { x ( t 1 ) x ( t 2 ) } = R x ( t 1 , t 2 ) = R x ( t 1 + τ , t 2 + τ ) = R x ( t 1 − t 2 , 0 ) ∀ τ ∈ R mathbb{E}left{xleft(t_{1}right) xleft(t_{2}right)right}=R_{x}left(t_{1}, t_{2}right)=R_{x}left(t_{1}+tau, t_{2}+tauright)=R_{x}left(t_{1}-t_{2}, 0right) forall tau in mathbb{R} E{x(t1​)x(t2​)}=Rx​(t1​,t2​)=Rx​(t1​+τ,t2​+τ)=Rx​(t1​−t2​,0)∀τ∈R

严平稳过程的条件比宽平稳苛刻得多，并且严平稳蕴含宽平稳过程，严平稳过程有如下要求:

$F_X\left(x_{t_1+\tau },\dots ,x_{t_n+\tau }\right)=F_X\left(x_{t_1},\dots ,x_{t_n}\right)$ for all $\tau ,t_1,\dots ,t_n\in \mathbb{R}$ and for all $n\in \mathbb{N}$

例子:

1. 设Y为一个R.V.，为0到2pi上的均匀分布，则如下随机过程(序列)是一个严平稳过程

$$X_t=\cos (t+Y)fort\in \mathbb{R}$$

2. 白噪声不一定是严平稳过程，例如，当omega为0到2pi上的均匀分布时，如下序列就不是严平稳的

$z_t=\cos (t\omega )(t=1,2,\dots )$

3. 平稳与否可以用ADF方法进行置信度检验

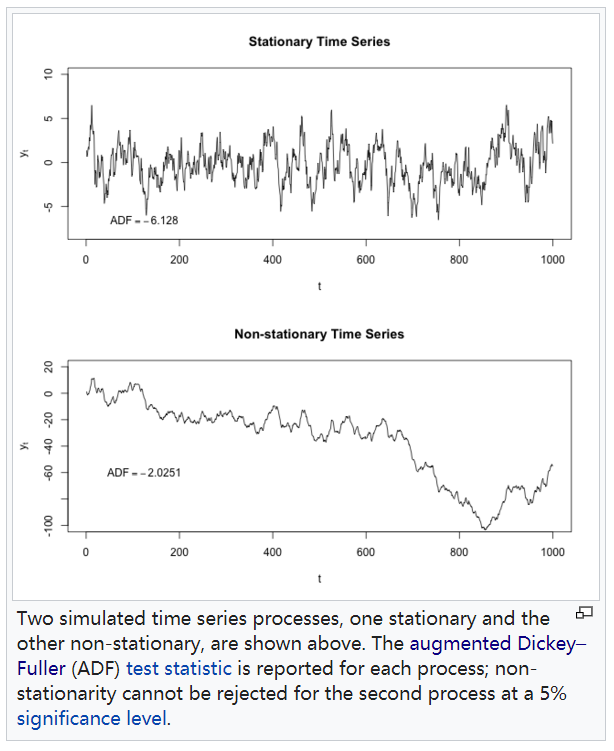
非平稳过程

以下简单介绍两种非平稳过程

1. 循环平稳过程

其定义此处步赘述

PAM信号就是典型的周期平稳过程而非宽平稳过程，从而也计算不了它的谱。

然而周期平稳过程与宽平稳过程之间只相差一层窗户纸，给周期平稳信号加上一个均匀分布的随机相位，周期平稳过程就可以变成宽平稳过程

2. 正交增量过程: 某过程前面的一部分和后面的一部分没有相关性

定义:

$$\begin{gathered} 取\forall t_1<t_2\le t_3<t_4 \\ 有(X_1-X_2)\perp (X_3-X_4) \end{gathered}$$

需要注意这两点:

• 正交增量过程比独立增量过程更加特殊: 当独立增量过程的均值为0时，进化为正交增量过程

• 一个随机过程为正交增量过程的充分必要条件是其自相关函数满足

$$R_X(s,t)=F(min(s,t))$$

为正交增量过程的充分必要条件是其自相关函数满足

$$R_X(s,t)=F(min(s,t))$$

最后

以上就是冷酷唇膏为你收集整理的随机过程总结(3)--一些非平稳过程平稳过程非平稳过程的全部内容，希望文章能够帮你解决随机过程总结(3)--一些非平稳过程平稳过程非平稳过程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。