1. 概率统计中的“矩”是什么?
对比物理的力矩,你会发现,概率论中的“矩”真的是很有启发性的一个词。
1.1 力矩
大家应该都知道物理中的力矩,我这里也不展开说细节了,用一幅图来帮助大家回忆一下:
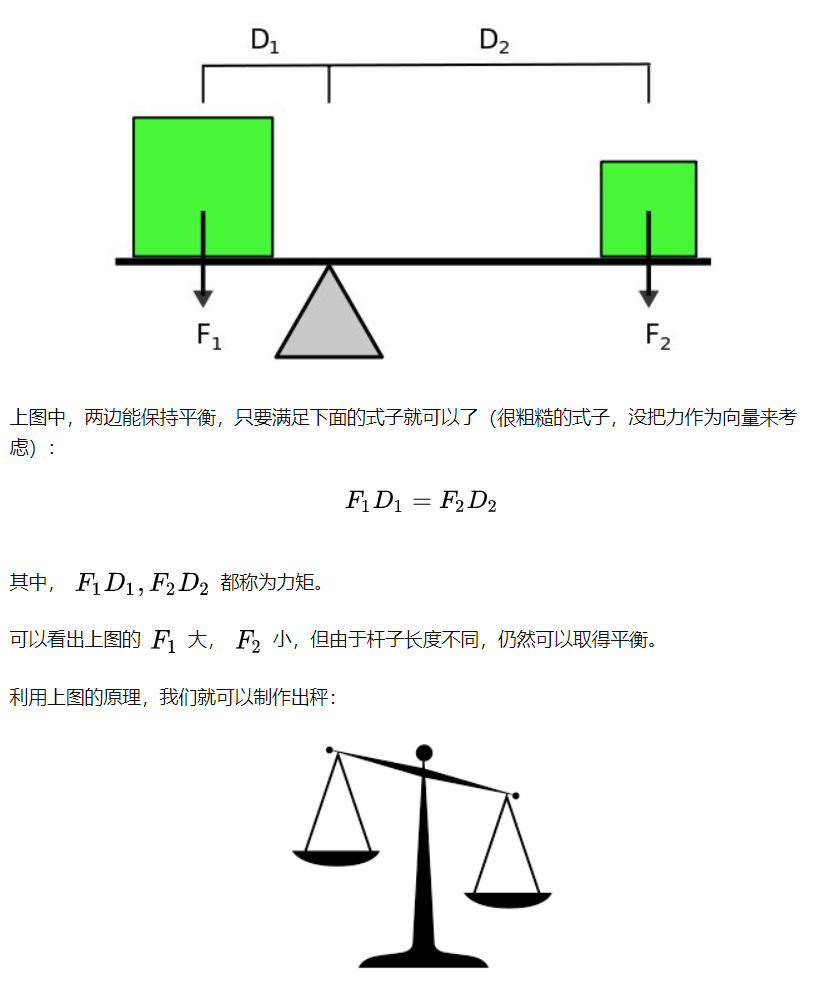
1.2 概率论中的“矩”
在概率论中,有一杆无处不在的“秤”。因为这把“秤”的存在,所以我们有了“矩”。
1.2.1 彩票的问题
福利彩票,,每一注两元钱,真是中国的良心啊,猪肉、房价都涨了多少了!?
每一注的中奖几率如下(胡诌的):
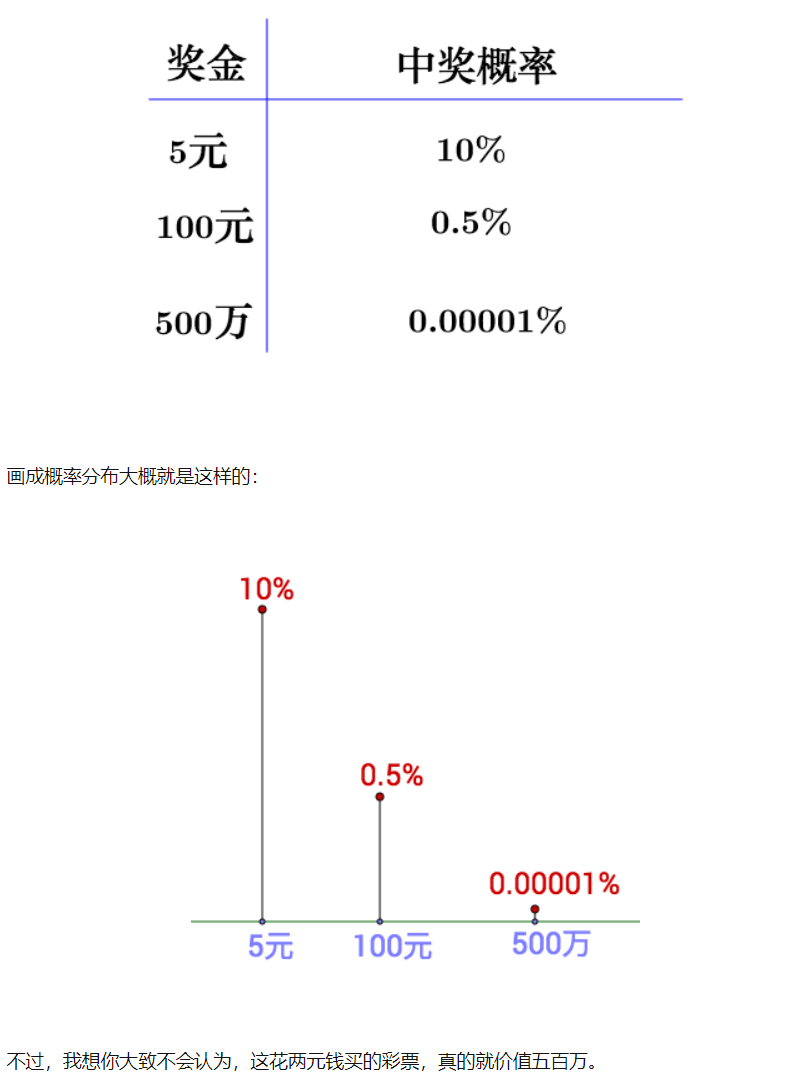
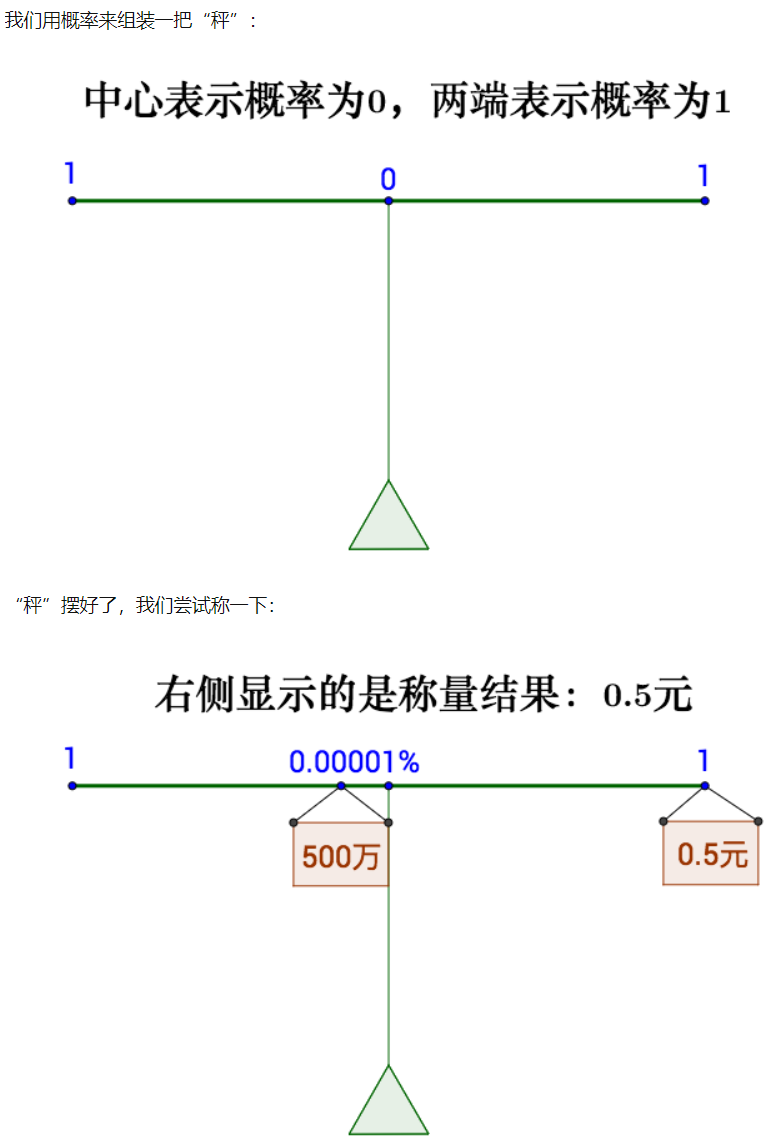
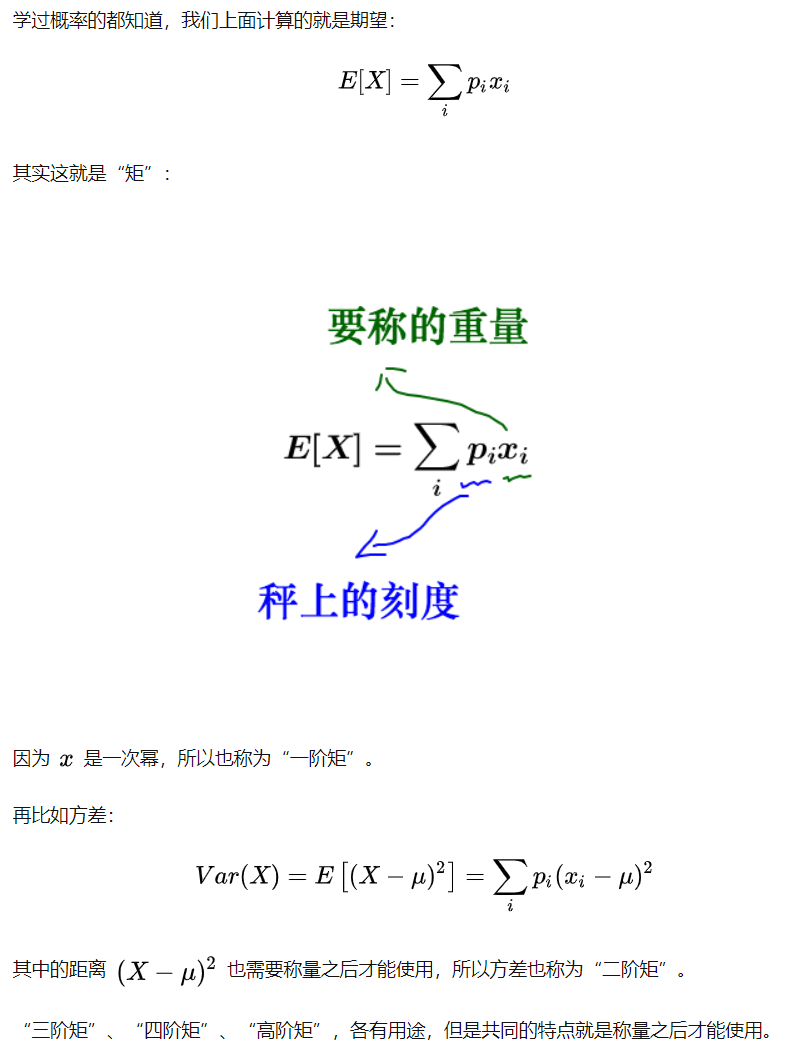
称量实际上是:
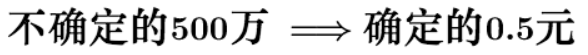

1.3 3 “矩”
%%%
比方说,我们感兴趣的是随机变量X。 矩是X的期望值,例如E(X),E(X²),E(X³)等。 第一矩是E(X), 第二矩是E(X²), 第三矩是E(X³), … 第n个矩是E(X ^ n)。
当然,我们非常熟悉前两个矩,均值μ= E(X)和方差E(X²)−μ²。它们是X的重要特征。 平均值是 平均值,方差是分布的分布程度。但是,必须有其他的特征来定义分布。例如,第三矩是分布的不对称性。第四关是尾巴有多沉、多厚。

这些矩告诉您有关分布的信息。
2. 什么是矩产生函数(MGF)?
关于产生/母函数https://blog.csdn.net/Anne033/article/details/109652192
顾名思义,MGF实际上是生成矩的函数 E(X),E(X²),E(X³),…,E(X ^ n)。也就是”矩“的母亲,够通俗吧。


这就是您从MGF那里获取时光的方式。
3. 证明,为什么第n个矩是MGF的第n个导数?
我们将使用泰勒级数证明这一点。

如果对③取另一种导数(因此取两次),则将得到E(X²)。 如果您采用另一个(三阶)导数,则将得到E(X³),依此类推…… 当我第一次看到矩生成函数时,我无法理解t在函数中的作用,因为t似乎是我不感兴趣的任意变量。但是,如您所见,t是辅助变量。我们引入t是为了能够使用演算(导数)并使(我们不感兴趣的)项为零。 等等…
但是我们可以直接了当,使用期望值的定义来计算。为什么我们还需要MGF?
4.为什么我们需要MGF?
为了方便,当然是我们希望MGF可以轻松计算矩。 但是,为什么MGF比定义期望值更容易? 在我的数学教科书中,他们总是问我“请找出计算二项式(n, p),泊松(λ),指数(λ),正态(0, 1)等的函数的矩。” 但是,他们从未真正向我展示过为什么MGF会如此有用以至于它们激发喜悦。
我认为以下示例会给您带来喜悦,最简单的示例显示MGF更容易:指数分布的MGF。
我们将从PDF开始。
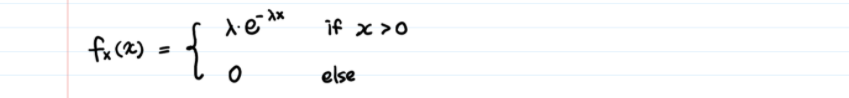
指数分布的PDF
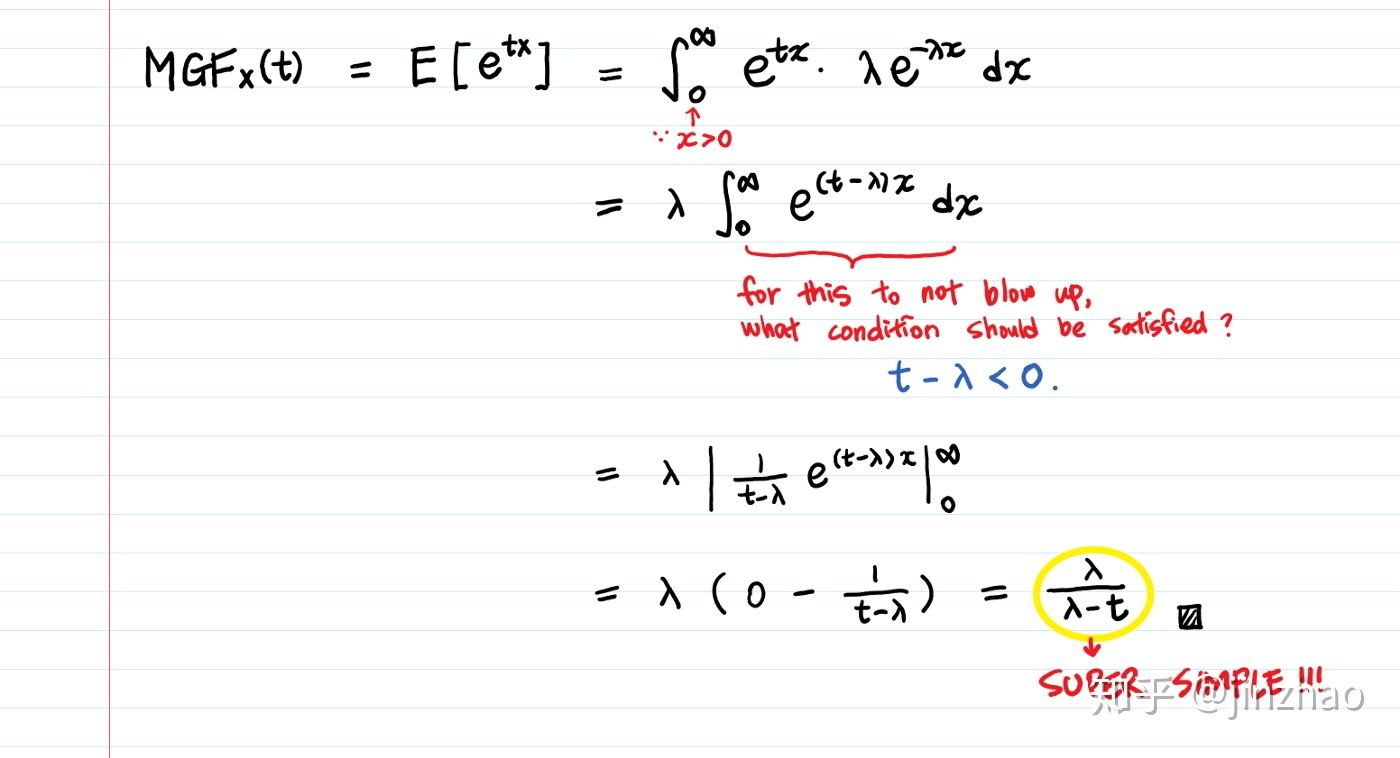
导出指数的MGF。

对于存在的MGF,应该存在期望值 E ( e t x ) E(e ^ tx) E(etx)。 这就是为什么“ t-λ<0”是要满足的重要条件的原因,因为,不满足积分将不会收敛。(这称为散度检验,这是在尝试确定积分是收敛还是发散时首先要检查的内容。) 一旦有了MGF: λ / ( λ − t ) λ/(λ-t) λ/(λ−t),计算矩就变成了求导数的问题,这比积分更容易直接计算期望值。
使用MGF,可以通过求导数而不是积分来查找矩!
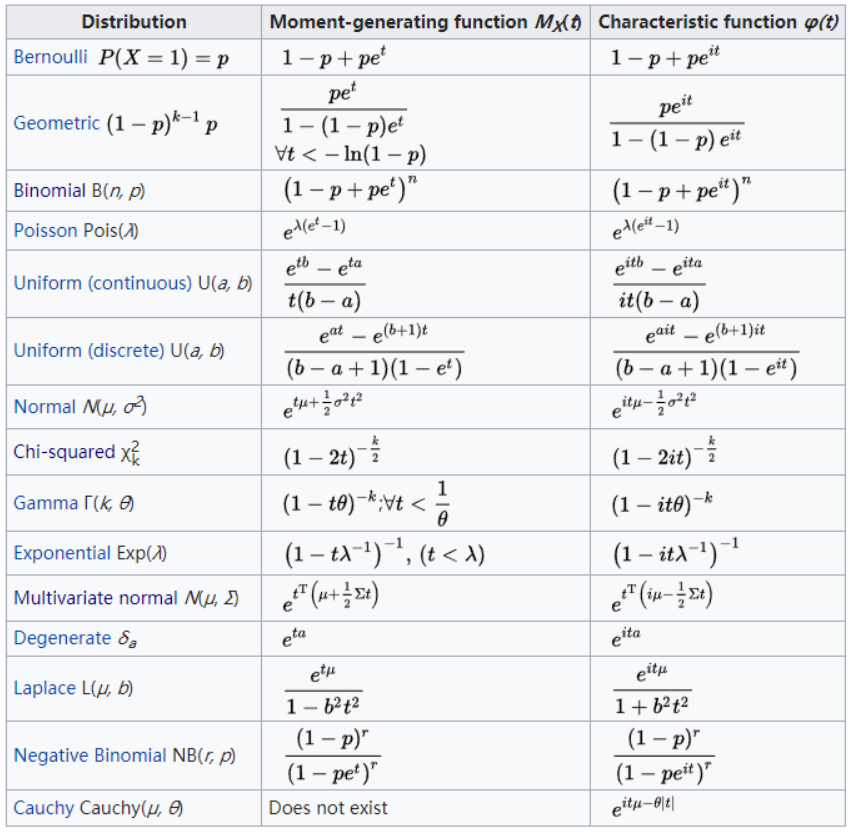
常见分布的MGF
MGF的属性

注意事项
对于任何有效的MGF,M(0)= 1,每当您计算MGF时,插入t = 0并查看是否得到1。
矩提供了一种指定分布的方法。例如,您可以在前两个矩(均值和方差)完全指定正态分布。当您知道分布的多个不同矩时,您将了解有关该分布的更多信息。如果有一个您没有认识的人,并且您知道他们的身高,体重,肤色,喜爱的爱好等,您仍然不一定完全了解他们,但是正在获得关于他们的越来越多的信息。
MGF的优点在于,一旦有了MGF(一旦存在期望值),您就可以得到第n个矩。MGF将随机变量的所有矩编码为一个函数,以后可以再次从中提取它们。
概率分布由其MGF唯一确定。如果两个随机变量具有相同的MGF,则它们必须具有相同的分布。
对于那些对术语“矩”感到好奇的人(像我一样):为什么一个矩称为矩?
分布的重要特征之一是它的尾巴有多沉重,尤其是对于金融风险管理而言。如果您还记得2009年的金融危机,那实际上就是无法解决罕见事件发生的可能性。风险管理人员低估了基金交易头寸中的许多金融证券的峰度(峰度在希腊语中是指“凸起”)。有时,假设的风险曲线平滑的随机分布可能会在其中隐藏凸起。而且我们可以检测到使用MGF的人员!
https://zhuanlan.zhihu.com/p/148408669
最后
以上就是哭泣哈密瓜最近收集整理的关于Moment Generating Function的全部内容,更多相关Moment内容请搜索靠谱客的其他文章。
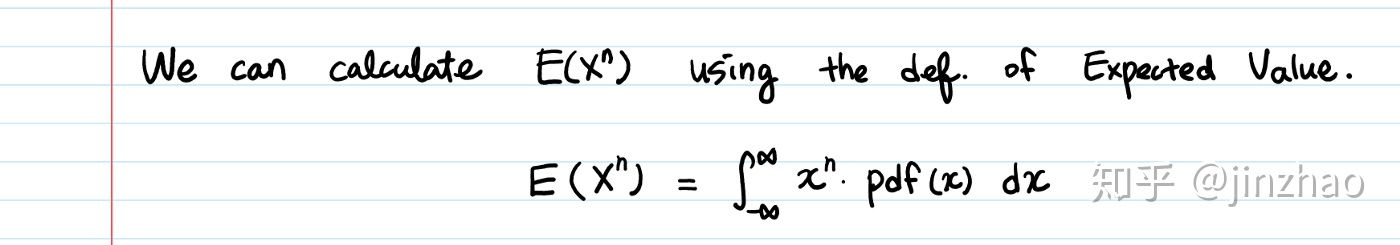








发表评论 取消回复