1、EM原理

EM本质是上是极大似然估计(MLE)概率模型有时即含有观测变量，又含有隐变量，如果概率模型的变量都是观测变量，只要show出测量数据，可以直接用极大似然估计法，或者用贝叶斯估计法估计模型参数。但是当模型含有隐变量时，就不能简单的用这些估计方法，EM算法就是含有隐变量的概率模型参数的极大似然估计法。
举个例子啥是隐变量，假设学校有100人，我们可以测出这100人的身高数据，我们都知道人的身高有时依赖于性别，但是不知道男女比例，这时男女比可以作为隐变量。

2、啥是混合高斯模型

先上表达式：
$$p({\mathbf{x}}_{\mathbf{j}})=\sum _{k=1}^{M}N({\mathbf{x}}_{\mathbf{j}}|{\mathbf{\mu }}_{\mathbf{k}},{\Sigma }_k)P(G_k),j=1,2,\dots ,N$$
上式是混合高斯模型的pdf，M表示高斯模型的数量（很多时候可视作分类簇数量），$P(G_k)$表示事件k发生的概率，${\mathbf{\mu }}_{\mathbf{k}},{\Sigma }_k$分别表示第k个高斯模型的均值和协方差矩阵。

3、EM算法求解GMM

先上似然函数：
$$L(\theta )=\prod _{i=1}^N\sum _{z}p(x_i,z;\theta )$$
取对数后：
$$l(\theta )=log\prod _{i=1}^N\sum _{z}p(x_i,z;\theta )=\sum _{i=1}^{N}log\sum _{z}p(x_i,z;\theta )$$
由于log函数满足凹函数性质，由一系列操作可以得到：
$$l(\theta )\ge \sum _{i=1}^N\sum _z{Q}_i(z_j)log\frac{p(x_i,z;\theta )}{Q_i(z_j)}$$
当$\frac{p(x_i,z;\theta )}{Q_i(z_j)}$为常数时，等号成立。
所以E-step:
$$Q_i(z_j)=p(z_j|x_i;\theta )$$
$Q_i(z_j)$表示第j样本对第i个高斯模型的’贡献率’（期望值）。
M-step就是在E-step上使上述函数值的期望取得最大时参数$\theta$的取值：
$$\theta :=argmaxl(\theta ）$$
接下来就是将GMM的pdf代入到EM算法步骤中：
第一步：对第i个样本对第j个高斯分布的贡献率：
$$Q_i(z=j)=P(z=j|x_i;\mu ,\Sigma )$$
第二步：根据E-step中的Q估计$\mu ,\Sigma$:
$${\mu }_l=\frac{{\sum }_i^N{Q}_i{x}_i}{{\sum }_i^N{Q}_i}$$
$${\Sigma }_j=\frac{{\sum }_i^N{Q}_j^{(i)}(x^{(i)}-{\mu }_j)(x^{(i)}-{\mu }_j{)}^T}{{\sum }_i^N{Q}_j^{(i)}}$$
对于j事件的发生概$P(G_j)$:
$$P(G_j)=\frac{{\sum }_i^N{Q}_j^{(i)}}{N}$$

4、实例

假设从学校学生中随机选取100位学生，测量这100位学生身高，既有男学生也有女生，现在已知测量数据。并且知道男性女性的身高均服从高斯分布$N({\mu }_1,\sigma 1),N(\mu 2,\sigma 2)$,
试估计参数${\mu }_1,\sigma 1,\mu 2,\sigma 2$以及男女比例$p_{male}和p_{female}$
第一步产生这一百个学生的身高数据：

N=100;                %样本数目 
mu1=170;              %男生身高均值
sigma1=0.5;           %男生身高均方根
mu2=160;              %女生身高均值
sigma2=0.1;           %女生身高均方根
pm=0.6;               %男生所占总数比例
pf=1-pm;              %女生所占总数比例
maleDatas=normrnd(mu1,sigma1,[1,N*pm]);%产生男生身高数据服从高斯随机分布
femaleDates=normrnd(mu2,sigma2,[1,N*pf]);%产生女生身高数据服从高斯随机分布
obsX=[maleDatas,femaleDates];
randIdx=randperm(N);
obsX=obsX(randIdx);    %混合男女身高数据
maxiter=100;           %最大迭代次数

第二步，用EM算法进行参数估计：

%% EM算法解GMM模型
% 第一步，初始化参数
estpm=0.5*ones(1,maxiter);                %待估男生比例
estpf=1-estpm;                            %待估女生比例
estmu1=mean(obsX)*ones(1,maxiter);        %待估男生身高均值
estsigma1=sqrt(std(obsX))*ones(1,maxiter);%待估男生身高均方根
estmu2=estmu1;                            %待估女生身高均值
estsigma2=estsigma1+rand*ones(1,maxiter); %待估男女生身高均方根
Q=zeros(2,N);                             %初始化贡献率
for i=2:maxiter
   % 第二步，E-step，计算贡献率
   for j=1:N
        k(1,j)=estpm(i-1)/(sqrt(2*pi)*estsigma1(i-1))*exp(-(obsX(j)-estmu1(i-1))^2/(2*estsigma1(i-1)^2));
        k(2,j)=estpf(i-1)/(sqrt(2*pi)*estsigma2(i-1))*exp(-(obsX(j)-estmu2(i-1))^2/(2*estsigma2(i-1)^2));
        p(j)=k(1,j)+k(2,j);
        Q(1,j)=k(1,j)/p(j);               %计算每个样本点对男生高斯分布贡献率
        Q(2,j)=k(2,j)/p(j);               %计算每个样本点对女生高斯分布贡献率
   end
   % 第三步，M-step，更新参数
   nk=sum(Q,2);
   estmu1(i)=Q(1,:)*obsX'/nk(1);
   estmu2(i)=Q(2,:)*obsX'/nk(2);
   estsigma1(i)=sqrt(sum(Q(1,:).*(obsX-estmu1(i)).^2)/nk(1));
   estsigma2(i)=sqrt(sum(Q(2,:).*(obsX-estmu2(i)).^2)/nk(2));
   estpm(i)=nk(1)/N;
   estpf(i)=nk(2)/N;
end

结果：


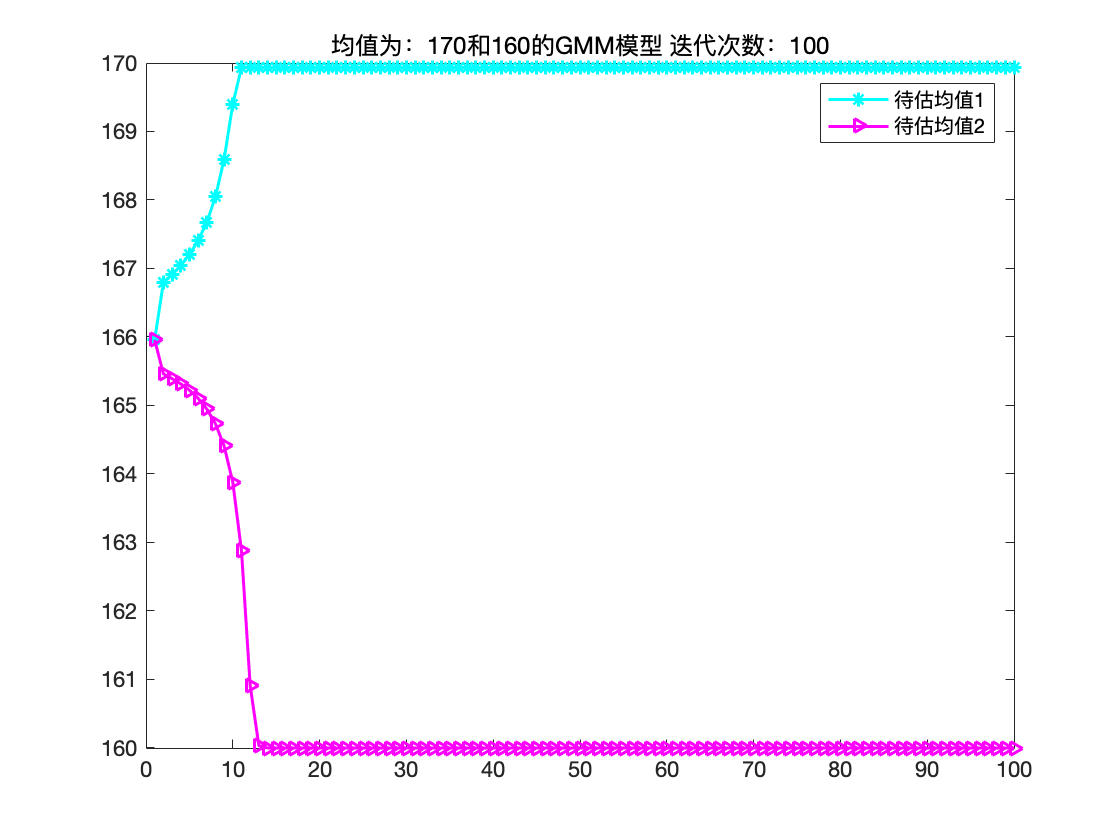
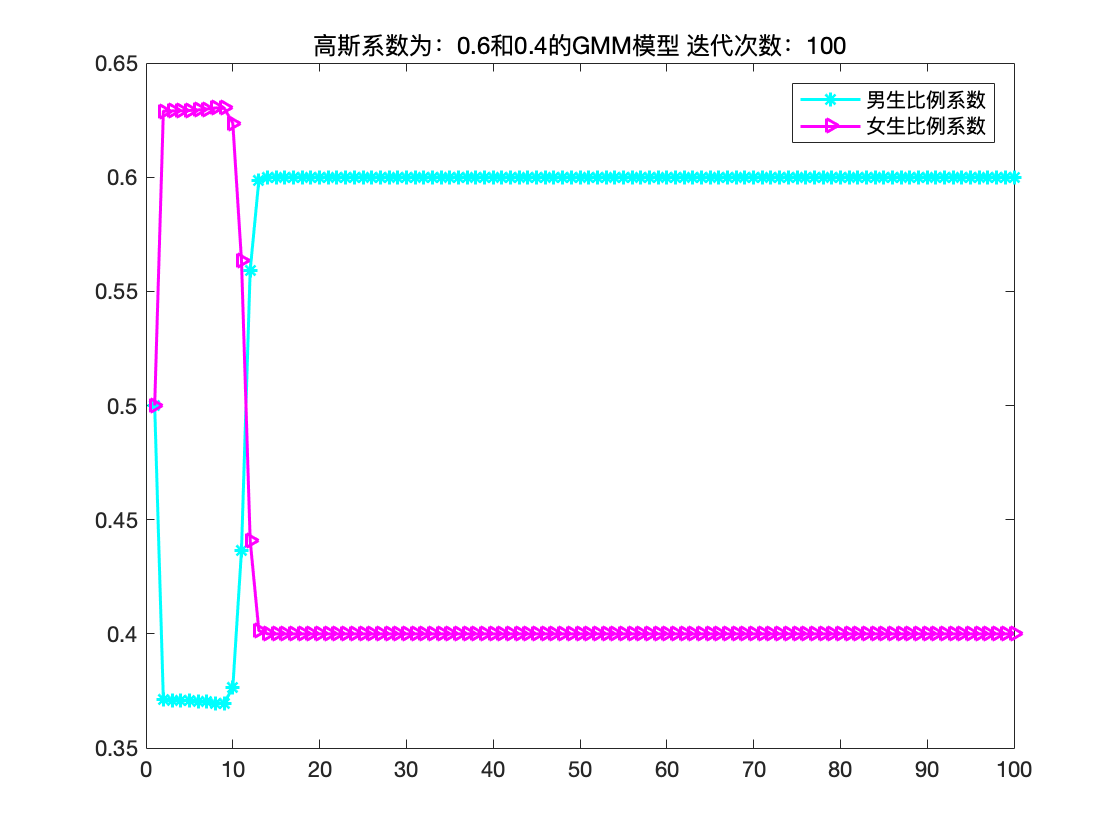
可以看出经过100次迭代后，GMM参数估计得到了很好的估计。

最后

以上就是妩媚奇异果为你收集整理的EM算法估计混合高斯模型(GMM)1、EM原理2、啥是混合高斯模型3、EM算法求解GMM4、实例的全部内容，希望文章能够帮你解决EM算法估计混合高斯模型(GMM)1、EM原理2、啥是混合高斯模型3、EM算法求解GMM4、实例所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。