随机过程

随机过程

1 概率论基础

（1）随机变量函数的概率密度

对于任意的单调函数$g(x)$,都有
$$f_Y(y)=f_X(x)|J{|}_{x=g^{-1}(y)}(J=\frac{dx}{dy})$$
对于非单调函数，可以根据单调性分段。

例: 考虑一个平方律检波的例子，假定输入输出的关系为
$$Y=b{X}^2$$
求Y的概率密度
解: 由于$Y$的值不可能为负，故$y<0$时，$f_Y(y)=0$。若$y>0$，这是对于任意的$y$，有两个$x$值与之对应，即
$x_1=\sqrt{y/b},x_2=-\sqrt{y/b}$ 由于$J_1=\frac{\mathrm{d}{x}_1}{\mathrm{d}y}=\frac{1}{2\sqrt{by}},J_2=\frac{\mathrm{d}{x}_2}{\mathrm{d}y}=-\frac{1}{2\sqrt{by}}$，因此
$$f_Y(y)=\frac{1}{2\sqrt{by}}\left[f_x(\sqrt{y/b})+f_X(-\sqrt{y/b})\right](y>0)$$

（2）基本公式

$$EX={\int }_{-\infty }^{+\infty }xf(x)\mathrm{d}x$$
$$DX=E(X-EX)=E{X}^2-E^{2}X$$
$$\mathrm{Cov}(X,Y)=E[(X-EX)(Y-EY)]=E[XY]-EXEY$$
$${\rho }_{XY}=\frac{\mathrm{Cov}(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$$

2 随机过程

(1)一维概率分布

$$F_x(x,t)=P(X(t)⩽x\}$$
如果$F_X(x,t)$的一阶导数存在，则定义
$$f_x(x,t)=\frac{\partial F_X(x,t)}{\partial x}$$
为随机过程$X(t)$的一维概率密度

(2)二维概率分布

对于任意的时刻$t_1,t_2$，以及任意两个实数$x_1,x_2$，定义
F x ( x 1 , x 2 , t 1 , t 2 ) = P { X ( t 1 ) ⩽ x 1 , X ( t 2 ) ⩽ x 2 ⟩ F_{x}left(x_{1}, x_{2}, t_{1}, t_{2}right)=Pleft{Xleft(t_{1}right) leqslant x_{1}, Xleft(t_{2}right) leqslant x_{2}rightrangle Fx​(x1​,x2​,t1​,t2​)=P{X(t1​)⩽x1​,X(t2​)⩽x2​⟩
为随机过程$X(t)$的二维概率分布，如果$F_X\left(x_1,x_2,t_1,t_2\right)$对$x_1,x_2$的偏导数存在，则定义
$$f_x\left(x_1,x_2,t_1,t_2\right)=\frac{{\partial }^2{F}_x\left(x_1,x_2,t_1,t_2\right)}{\partial x_1\partial x_z}$$
为随机过程$X(t)$的二维概率密度。

(3)随机过程的数字特征

均值

$$m_X(t)=E[X(t)]={\int }_{-\infty }^{+\infty }x{f}_x(x,t)\mathrm{d}x$$

方差

$${\sigma }_X^2(t)=E\left\{{\left[X(t)-m_X(t)\right]}^2\right\}=E\left[X^2(t)\right]-m_X^2(t)$$

自相关函数与协方差函数

对于任意两个时刻$t_1,t_2$，定义

$$R_X\left(t_1,t_2\right)=E\left[X\left(t_1\right)X\left(t_2\right)\right]={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{x}_1{x}_{2}f\left(x_1,x_2,t_1,t_2\right)\mathrm{d}{x}_1\mathrm{d}{x}_2$$
为随机过程$X(t)$的自相关函数。自相关就是函数和函数本身的相关性，当函数中有周期性分量的时候，自相关函数的极大值能够很好的体现这种周期性
相关性的描述除了用相关函数外，有时也用协方差函数。定义
K x ( t 1 , t 2 ) = E { [ X ( t 1 ) − m X ( t 1 ) ] [ X ( t 2 ) − m X ( t 2 ) ] } K_{x}left(t_{1}, t_{2}right)=Eleft{left[Xleft(t_{1}right)-m_{X}left(t_{1}right)right]left[Xleft(t_{2}right)-m_{X}left(t_{2}right)right]right} Kx​(t1​,t2​)=E{[X(t1​)−mX​(t1​)][X(t2​)−mX​(t2​)]}
为随机过程$X(t)$的协方差函数，协方差函数也可以表示为
$$\begin{array}{rl}{K}_X\left(t_1,t_2\right)& =E\left[X\left(t_1\right)X\left(t_2\right)\right]-m_X\left(t_1\right)m_X\left(t_2\right)\\ & =R_X\left(t_1,t_2\right)-m_X\left(t_1\right)m_X\left(t_2\right)\end{array}$$
相关运算从线性空间的角度看其实是内积运算，而两个向量的内积在线性空间中表示一个向量向另一个向量的投影，表示两个向量的相似程度，所以相关运算就体现了这种相似程度。

（4）广义平稳随机过程

如果随机过程$X(t)$的均值为常数，自相关函数只与$tau=t_{1}-t_{2}$有关，即
$$\begin{array}{l}{m}_X(t)=m_X\\ R_X\left(t_1,t_2\right)=R_X(\tau ),\tau =t_1-t_2\end{array}$$
则称随机过程$X(t)$是广义平稳的

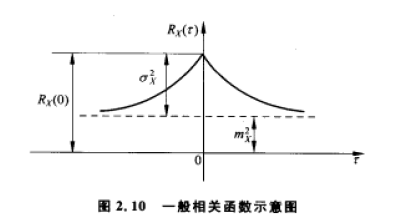
（5）平稳随机过程的相关系数和相关时间

相关系数

$$r_X(\tau )=\frac{K_x(\tau )}{{\sigma }_X^2}=\frac{R_X(\tau )-m_X^2}{{\sigma }_X^2}$$

相关时间

$$\left|r_X\left({\tau }_0\right)\right|⩽0.05$$

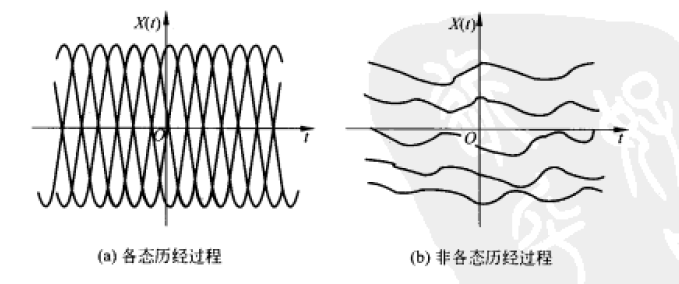
(6)各态历经过程

 　　各态历经随机过程一个样本函数经历了随机过程所有可能的状态，通过对一条样本函数的观测就可以估计出随机过程的均值、方差和相关函数
　　对大多数的平稳随机过程而言，都具有各态历经性
　　

3 随机过程的联合分布和互相关函数

互相关函数

$$R_{XY}\left(t_1,t_2\right)=E\left[X\left(t_1\right)Y\left(t_2\right)\right]={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }xy{f}_{xy}\left(x,y,t_1,t_2\right)\mathrm{d}x\mathrm{d}y$$

互协方差函数

K X Y ( t 1 , t 2 ) = E { [ X ( t 1 ) − m x ( t 1 ) ] [ Y ( t 2 ) − m X ( t 2 ) ] } K_{X Y}left(t_{1}, t_{2}right)=Eleft{left[Xleft(t_{1}right)-m_{x}left(t_{1}right)right]left[Yleft(t_{2}right)-m_{X}left(t_{2}right)right]right} KXY​(t1​,t2​)=E{[X(t1​)−mx​(t1​)][Y(t2​)−mX​(t2​)]}

互协方差函数与互相关函数的关系

$$K_{XY}\left(t_1,t_2\right)=R_{XY}\left(t_1,t_z\right)-m_X\left(t_1\right)m_X\left(t_z\right)$$

广义联合平稳

如果
$$\begin{array}{l}{m}_X(t)=m_x\\ m_Y(t)=m_Y\\ R_{XY}\left(t_1,t_2\right)=R_{XY}(\tau ),\tau =t_1-t_2\end{array}$$
则称$X(t)$与$Y(t)$是广义联合平稳的

联合平稳随机过程互相关函数性质

(1)

$$\begin{array}{l}{R}_{XY}(-\tau )=R_{YX}(\tau )\\ K_{XY}(-\tau )=K_{YX}(\tau )\end{array}$$
因为
$$R_{XY}(-\tau )=E[X(t-\tau )Y(t)]=E[Y(t)X(t-\tau )]=R_{YX}(\tau )$$

(2)

$$\begin{array}{l}{\left|R_{XY}(\tau )\right|}^2⩽R_X(0)R_Y(0)\\ 2R_{XY}(\tau )⩽R_X(0)+R_Y(0)\\ {\left|K_{XY}(\tau )\right|}^2⩽{\sigma }_X^2{\sigma }_Y^2\end{array}$$

(3)

若$X(t)$与$Y(t)$是联合平稳的，则$Z(t)=X(t)+Y(t)$是平稳的，且
$$R_Z(\tau )=R_X(\tau )+R_Y(\tau )+R_{XY}(\tau )+R_{YX}(\tau )$$

4 随机过程功率谱

实质是推广的频谱分析，使用了截尾函数，使得信号满足绝对可积的狄里克雷条件

最后

以上就是笑点低招牌为你收集整理的随机过程的全部内容，希望文章能够帮你解决随机过程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。