首先我们要知道,什么是多维随机变量?:
意思就是,w是样本空间里的一个事件,这个w对应着两个属性(平时都是一个w对应一个属性)这个X(w)就是一个常数,也就是概率了。
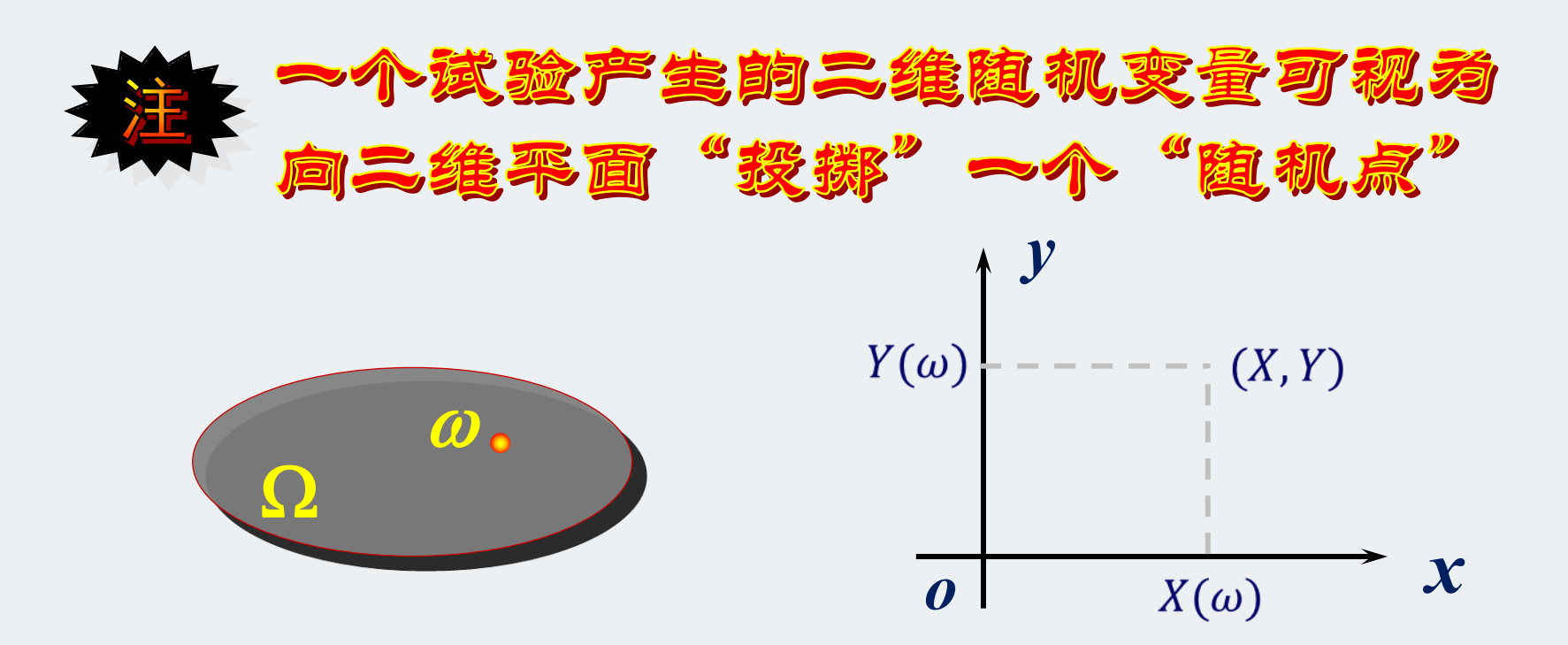
我们过去的样本空间就像是一条线,现在变成一个面了,也就有了两个要素。
二维随机变量的联合分布函数:

确实很像向量呀。
定义:设(x,y)x,y属于R,定义F(x,y)=P(X<x,Y<y)则称F(x,y)是二维r.v(X,Y)的累积分布函数,即X与Y的联合分布函数。
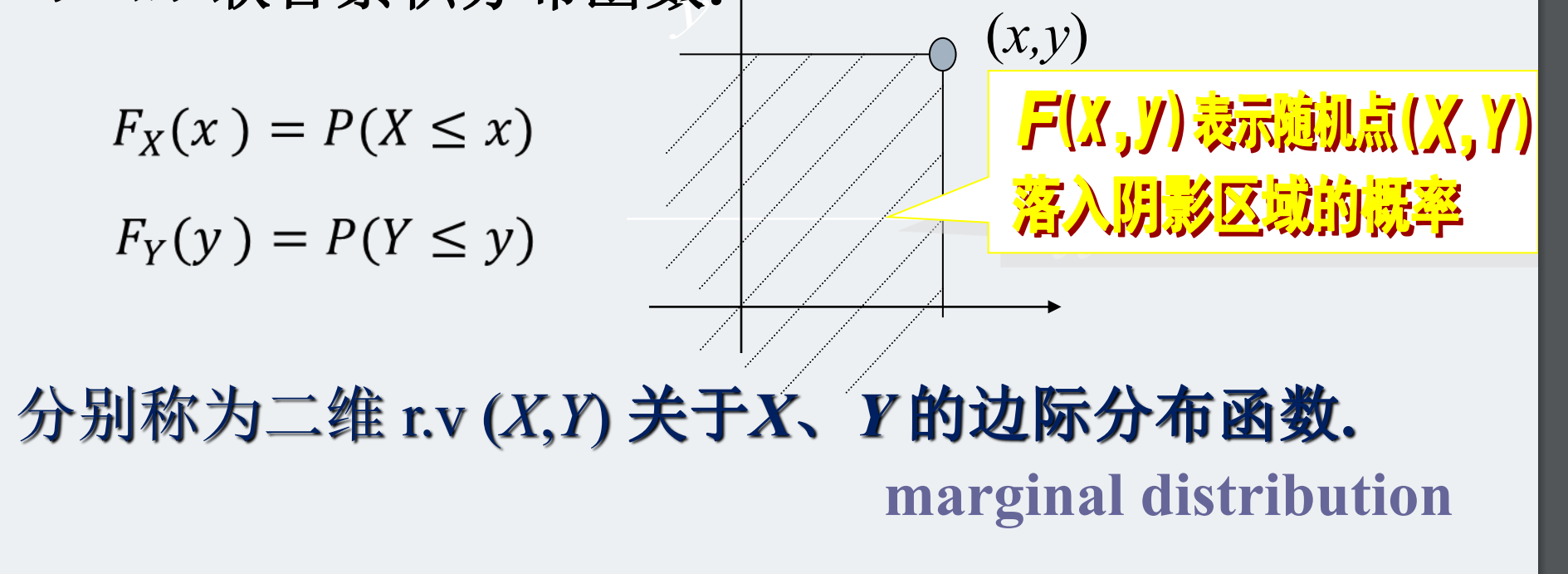
Fx(x)=P(X<x),Fy(y)=P(Y<y)分别叫二维r.v(X,Y)关于X,Y的边际分布函数。
F(x1<X<x2,y1<Y<y2)=F(x2,y2)-F(x2,y1)-F(x1,Y2)+F(x1,y1)可以画图证明。:

接下来就是一些函数性质:
 我们要证明一个函数是联合分布函数,4项性质都要满足。不可以省掉第4项:
我们要证明一个函数是联合分布函数,4项性质都要满足。不可以省掉第4项:

就比如这个,满足前3项不和第4项就不可以。
现在我们来思考一个问题:边际函数和联合函数有什么关系:

假如这个变量是离散的怎么办?:

当然他也有自己的特征:

那么,离散的边际分布列是怎样的呢:

就比如说P(X=xi),就是把所有X=xi的情况加起来,也就是pi(所有pij其实就是pi*pj,现在所有的都加起来了,pj的和是1,也就成了pi),Y的情况同理:

接下来就要看密度函数了:
r.v(X,Y)的分布函数为:F(x,y)=P(X<x,Y<y)
若存在非负可积函数使得:F(x,y)=||f(x,y)dxdy,(|是积分符号)则f(x,y)就是他的密度函数。

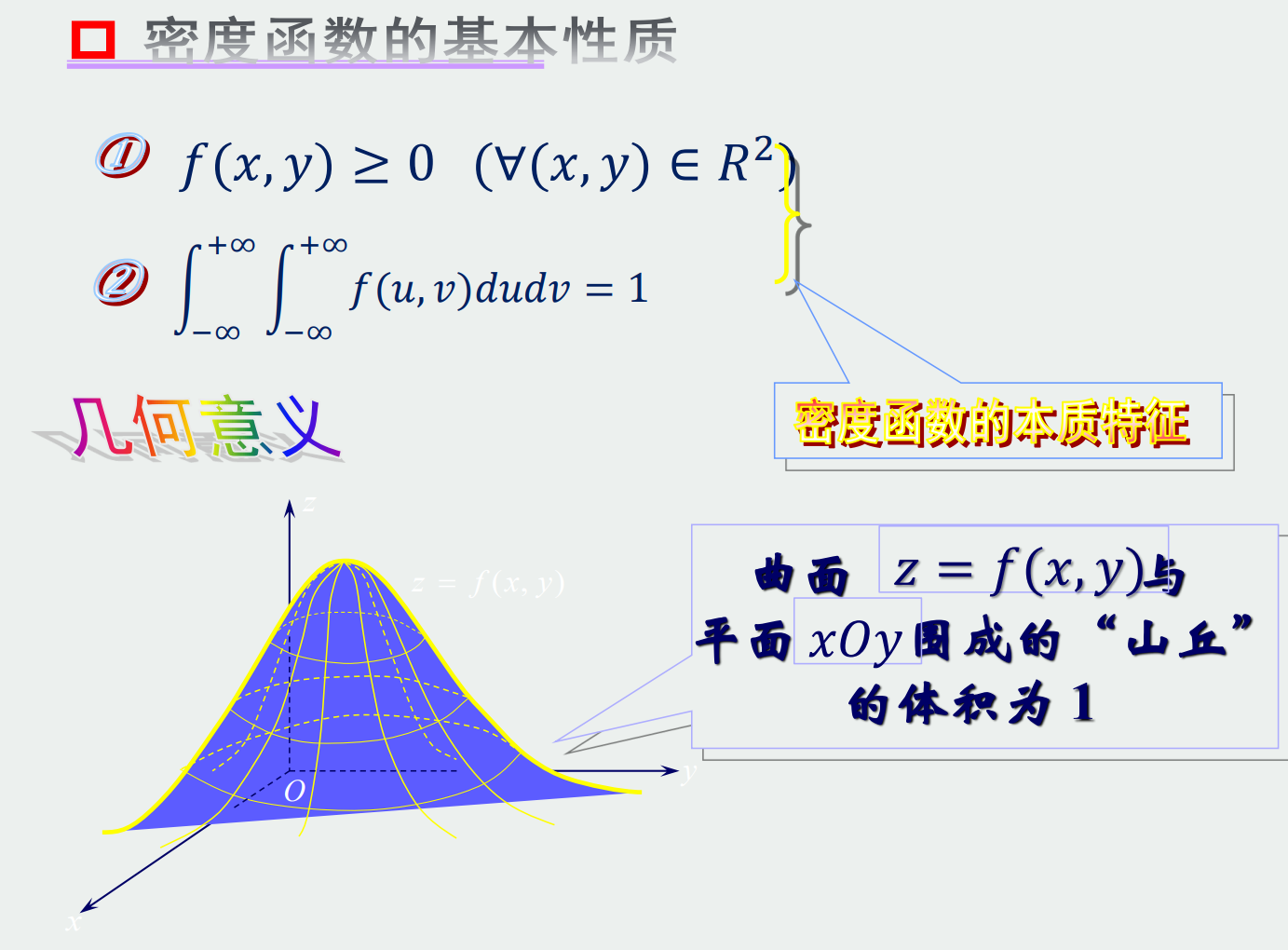
就像原来的密度函数面积是1一样。

很显然,一小块面积对应的体积就是这个面积对应的概率。积两次就是分布函数,导两次就是密度函数。
只知道X,Y的函数怎么办?:

u就是x,v就是y.求个个Fx,Fy就是先把y,x这些已经确定范围是R的积完,再积范围限制的。密度函数就是只要积y,x这些范围固定了的。
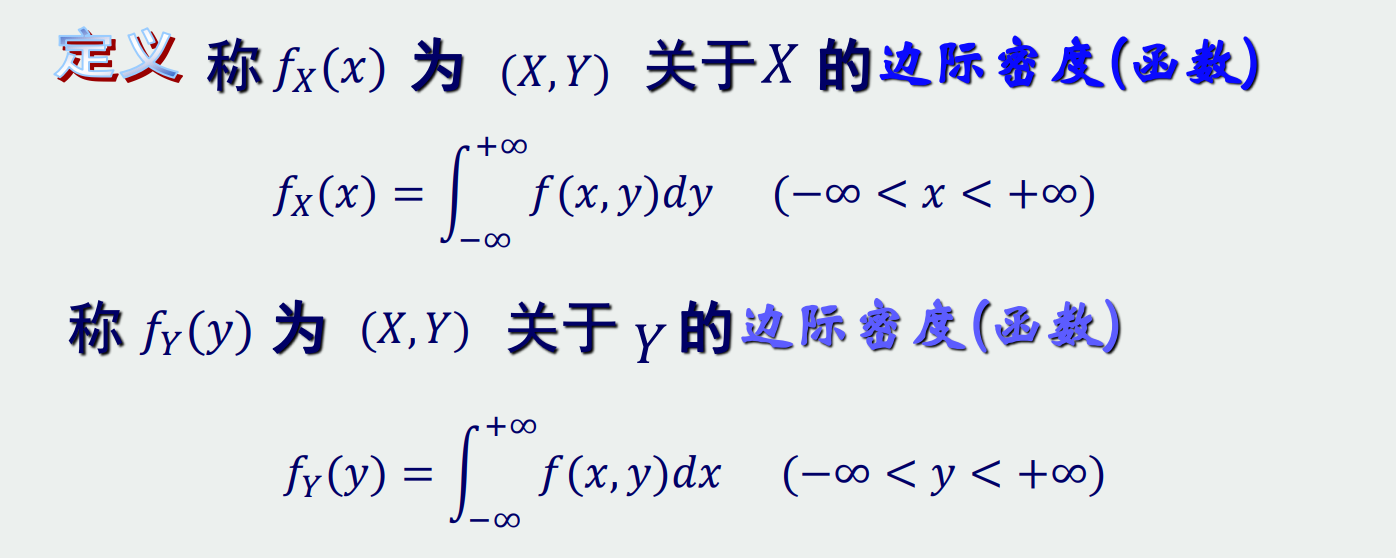
现在我们来学习一下二维的各种分布:
二维均匀分布:

二维正态分布:
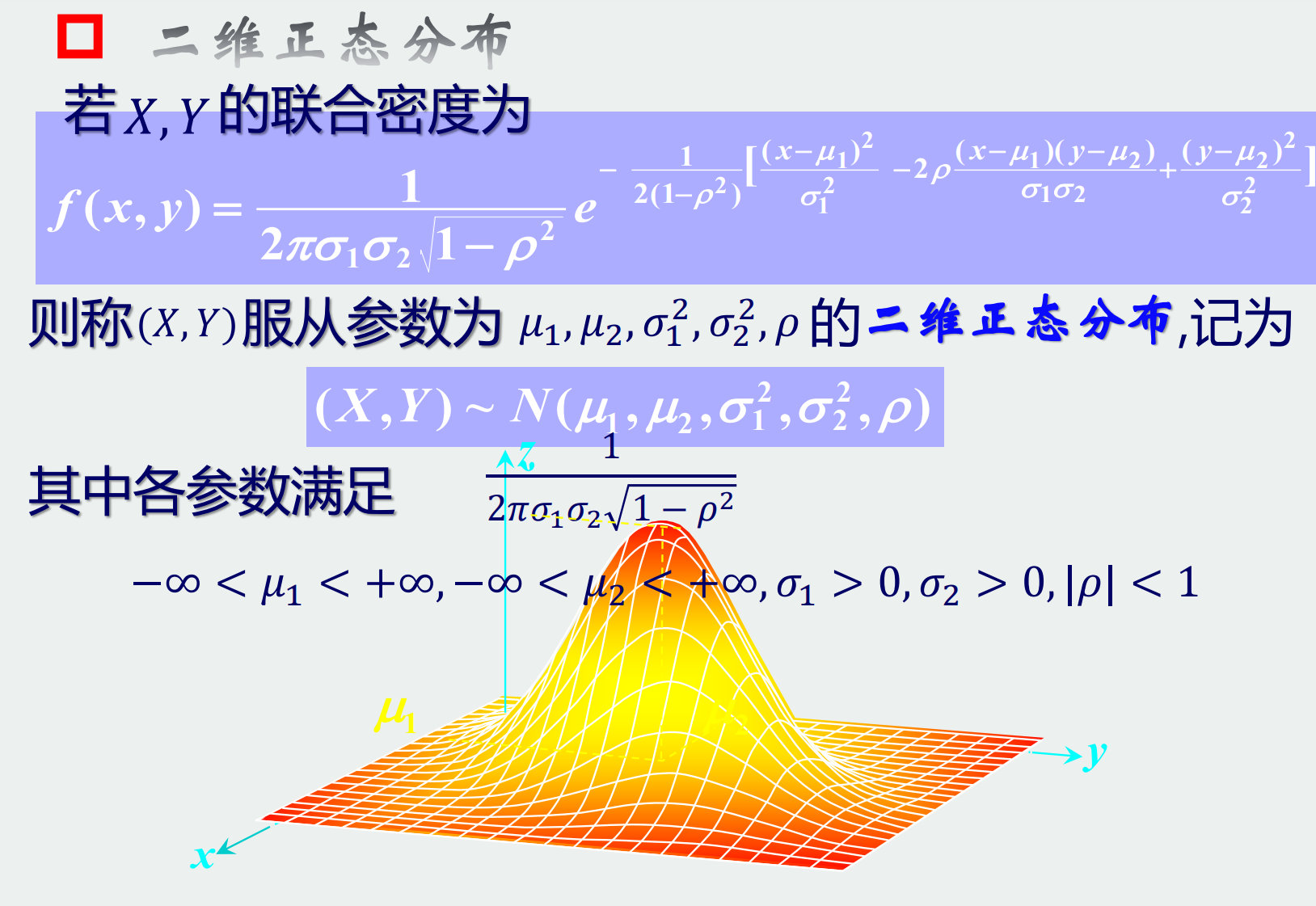
这个式子复杂的逆了天了。我们可以用它的边际分布:

他的边际分布就是一般的正态分布。
注意:均匀分布的边际函数不一定是均匀分布!可以这样想:我的高度都是一样的,但x对应的y的范围可能不一样大,y的范围大fx就大,范围小fx就小,那还能叫均匀分布吗?
现在,我们来学习一下多维随机变量中随机变量的独立性:

由此可以看到,只要x,y各自的边际函数相乘是F(x,y)(二者的总概率)

下面有详细的证明:

F才是概率,但用f乘也可以,后面会证
离散的怎么办呢?:

如何用密度函数证明独立?:

可以这样想:我取一块很小很小的正方形,给左右两边乘上。左边就是那一小片面积对应的概率,也就是F(x<X<x+x',y<Y<y+y'),右边给fx乘上正方形的x,fy乘y,也就是Fx(x<X<x+x')Fy(y<Y<y+y'),就成了。
现在我们回忆一下我们之前学的多维正态分布,p是干什么的?:

之前一直都是独立的,假如不独立怎么办?:

那么我就可以有这样的定义:


都只是套用了原来的知识,没新东西。
离散的知道了,那连续的呢?:
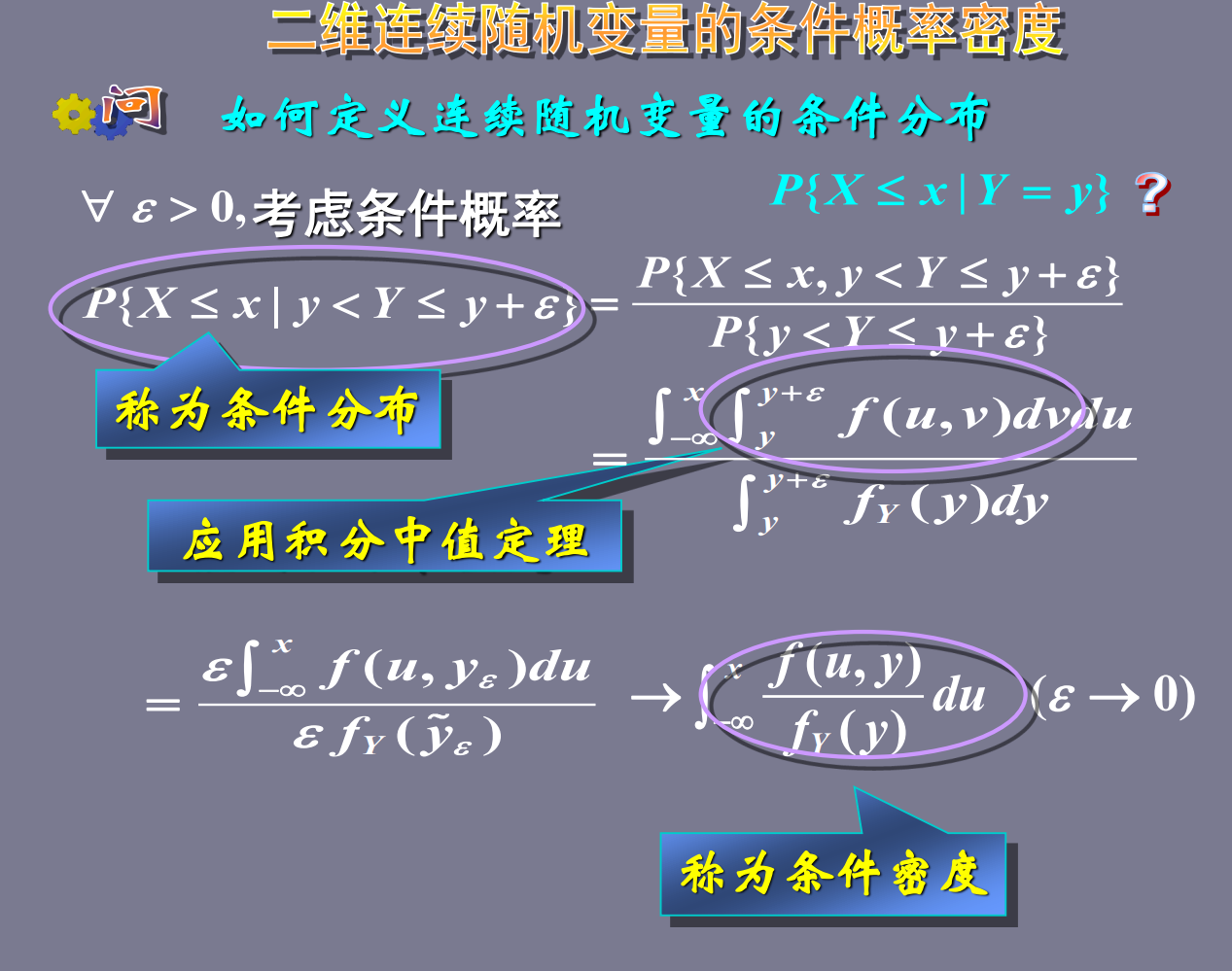
和一般的同样的道理。用二者共同的概率除以y的概率,最后积起来就是了。不过要注意这里用了y的密度函数作为概率,所以谁他要趋近于0.


这种条件的分布函数用图表示是什么样的呢?我们想象一个立体的函数图(f(x,y)的图),在Y=y的情况下也就像是在Y=y的地方横了一个面,切出来的就是fx|y(x|y)的图像。
全概率和边际分布,条件分布的关系:

可以看到,我们原来说“全概率函数不能直接用边际函数表示”,就是因为P(xy)不一定等于p(x)p(y),x,y可能是不独立的,f(y|x)可能不等于f(y)。现在有了条件函数就可以了。

X,Y的条件概率到此结束了,现在我们来学学X,Y的函数的分布:

可以这样想:f(X=x,Y=y)=fx(X=x)fy(Y=y),f(X=z-y,Y=y)=fx(X=z-y)fy(Y=y),|f(X=z-y,Y=y)=|fx(X=z-y)fy(Y=y)=fz(z)
这里给个例子:

注意:指数分布是连续变量的密度函数,泊松分布是离散分布的各个项的值。
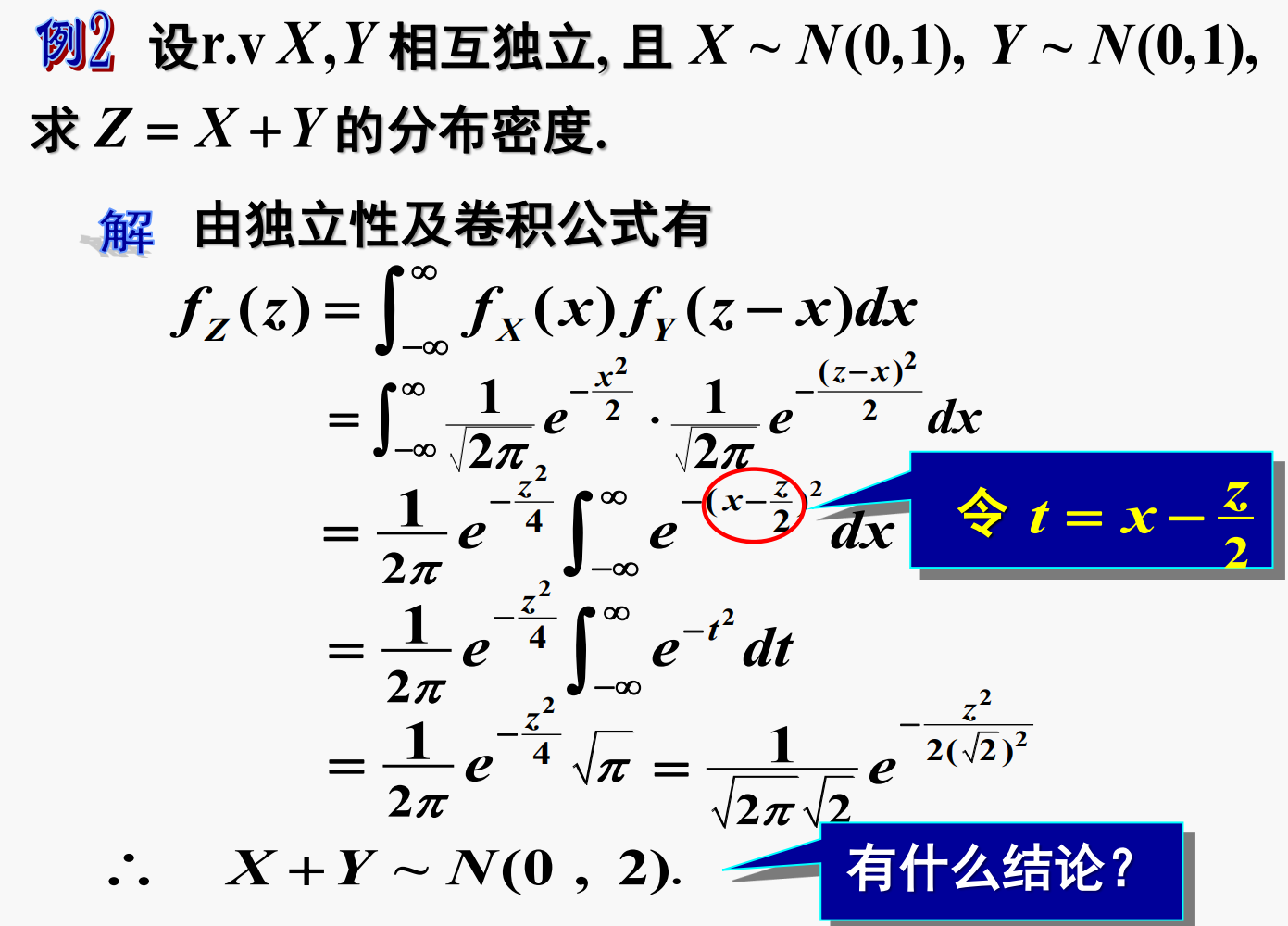
由此可以推出:

假如X,Y是离散型的话怎么办?:

和连续的一样,都是把所有可能的都加起来。

P就是泊松分布。
接下来是几个重要的结论:

P是泊松,B是二项分布(X和Y都是二项分布,概率都是P,X+Y的概率当然就是M+N次实验P的概率啦),N是正态分布。
极值Max,min就是X和Y最大/最小是Z的意思。

独立同分布就是服从同一分布,并且相互独立。那当然大家的Fx(x)都是一样的了。
假如是连续的,我想要求它的密度怎么办:
 F(Z)的算法还是一样的,接下来要求f(Z)的话就要求导。
F(Z)的算法还是一样的,接下来要求f(Z)的话就要求导。
最后
以上就是成就奇异果最近收集整理的关于概率论:多维随机变量的全部内容,更多相关概率论内容请搜索靠谱客的其他文章。








发表评论 取消回复