线性回归-梯度下降法

线性回归-最小二乘法

1、梯度下降法

前文在求解损失函数的最小值的时候，使用到了最小二乘法，但是有一定的缺陷，当数据量大的时候，计算量就变大了，效率就体现不出来了。梯度下降法是求解目标函数最优解的一个比较通用的方法。
梯度： 在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。沿着梯度向量的方向更易找到函数最大值，沿着梯度向量相反的方向更易找到最小值。

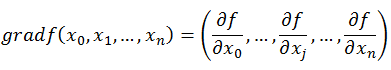
2、一元线性回归中的梯度下降

可以使用：$x=x-\eta \frac{df}{dx}$ ，来不断寻求最小值。其中
$\eta$为学习率(learning rate)。学习率的取值是很重要的；它是梯度下降法的一个超参数；学习率的取值影响获得最优解的速度；如果取值不合适（取值过大），甚至无法得到最优解。梯度上升可以使用：$x=x+\eta \frac{df}{dx}$，来寻找最大值。
学习率$\eta$的作用效果：

1. $\eta$太小，减慢收敛学习的速度，当问题规模大的时候，效率太低。
   

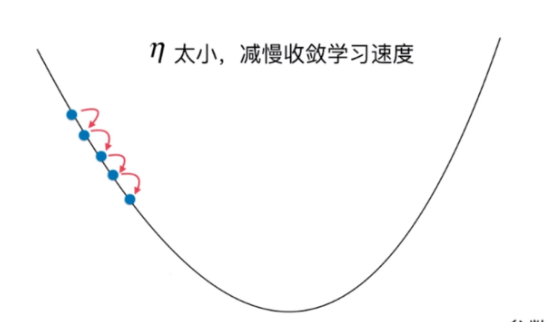
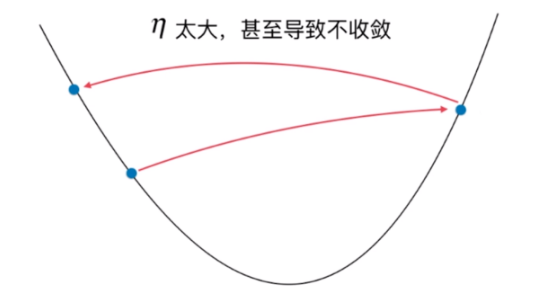
2. $\eta$太大，甚至导致不收敛
   
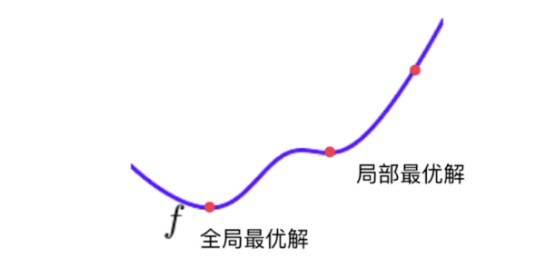
   有时候存在多个极值的时候，需要随机初始化点多次运行，来寻找最值。
   

3、多元线性回归中的梯度下降，批量梯度下降法（Batch Gradient Descent, BGD）

损失函数： $J={\sum }_{i=1}^m(y^i-{\hat{y}}^i{)}^2$

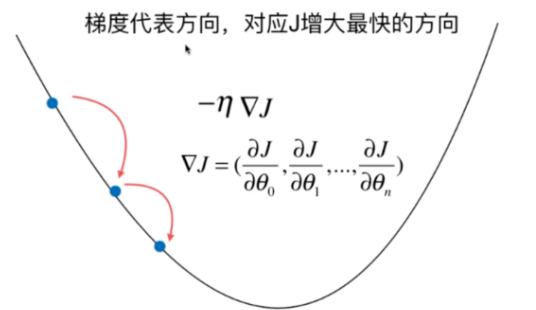
此时梯度： ${▽}_J=(\frac{\partial J}{\partial {\theta }_0},\frac{\partial J}{\partial {\theta }_1},\frac{\partial J}{\partial {\theta }_2},...,\frac{\partial J}{\partial {\theta }_n})$,表示J增大最快的方向。下图是一个具有两个特征的梯度下降可视化。

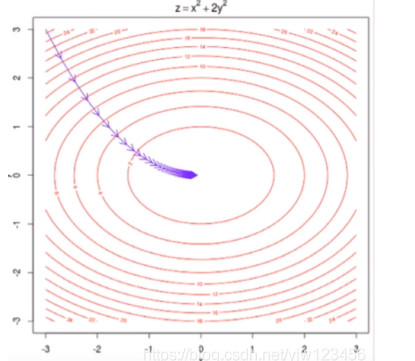
要使损失函数$J={\sum }_{i=1}^m(y^i-{\hat{y}}^i{)}^2$尽可能小，这里
${\hat{y}}^i={\theta }_0+{\theta }_1{X_1}^i+{\theta }_1{X_1}^i+{\theta }_2{X_2}^i...+{\theta }_n{X_n}^i$ ，
使${\sum }_{i=1}^m{(y^i-{\theta }_0+{\theta }_1{X_1}^i+{\theta }_1{X_1}^i+{\theta }_2{X_2}^i...+{\theta }_n{X_n}^i)}^2$
尽可能小。
此时梯度就是使J对$\theta$的每个维度求偏导，可以写成：






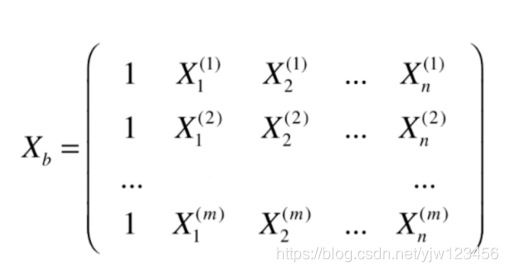
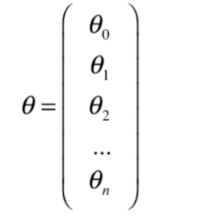
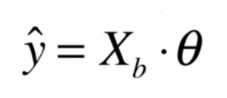
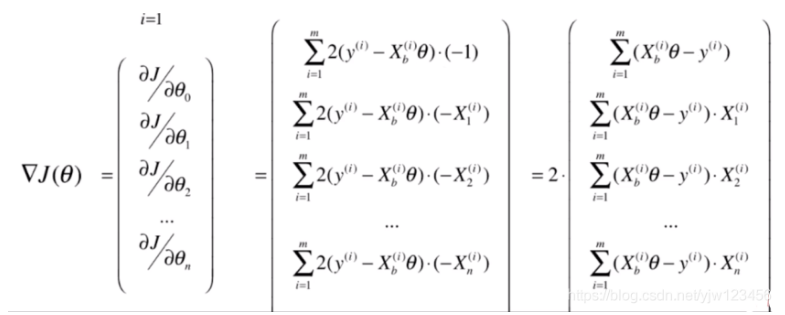
这里还注意到，这里有个求和符号，意味着梯度的大小是与样本数量m 有关的，样本数量越大，梯度也就越大。这样显然是不合理的，因此，我们让整个梯度值都除以一个m：

这样相当于把我们的损失函数前面也乘了一个$\frac{1}{m}$:
$J(\theta )=\frac{1}{m}{\sum }_{i=1}^m(y^i-{\hat{y}}^i{)}^2$
或者：
$J(\theta )=\frac{1}{2m}{\sum }_{i=1}^m(y^i-{\hat{y}}^i{)}^2$
有了损失函数和梯度，传入一个起始的$\theta$和学习率$\eta$，就可以自动寻找损失函数的最值了。
$\{\begin{array}{l}J(\theta )=\frac{1}{2m}{\sum }_{i=1}^m(y^i-{\hat{y}}^i{)}^2\\ \theta =\theta -\eta {▽}_{J(\theta )}\\ {▽}_{J(\theta )}=(\frac{\partial J}{\partial {\theta }_0},\frac{\partial J}{\partial {\theta }_1},\frac{\partial J}{\partial {\theta }_2},...,\frac{\partial J}{\partial {\theta }_n})={X_b}^T(X_b\theta -y)\\ \hat{y}=X_b\theta \end{array}$
$X_b$上边已经给出。
为了防止梯度太大，最好先将X进行归一化(最值归一化、均方误差归一化)处理。否则，有可能找不到损失函数的最值。这里对比一下最小二乘法是不需要数据归一化的，因为它是用方程的方法来计算的。scikit-Learn

# 使用scikit-learn 封装好的函数，进行数据的归一化。
from sklearn.preprocessing import StandardScaler
st = StandardScaler()
st.fit(X_train)
X_train_standard = st.transform(X_train)

4、随机梯度下降（Stochastic Gradient Descent, SGD）

之前的批量梯度下降法是对所有的样本求梯度，当数据规模很大的时候，整个计算过程是很耗时的。有一种办法，每次只对一个样本求梯度，或者每次只对若干个样本求梯度，这种方法就叫做随机梯度下降法 。

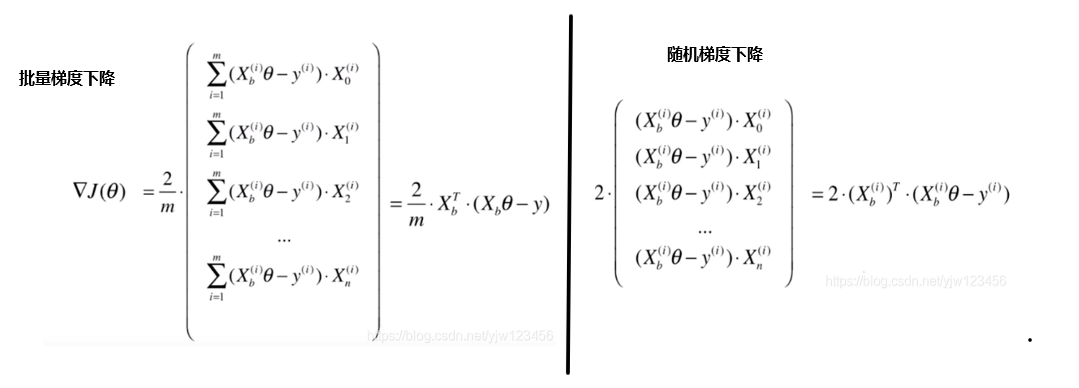
随机梯度下降法无法保证得到的方向一定是损失函数减小的方向，更不能保证是减小最快的方向，所以我们的搜索路径形成了这样的一种趋势。也就是它具有随机的特点，但是实验结论告诉我们，它最终依然可能到达最小值的附近。

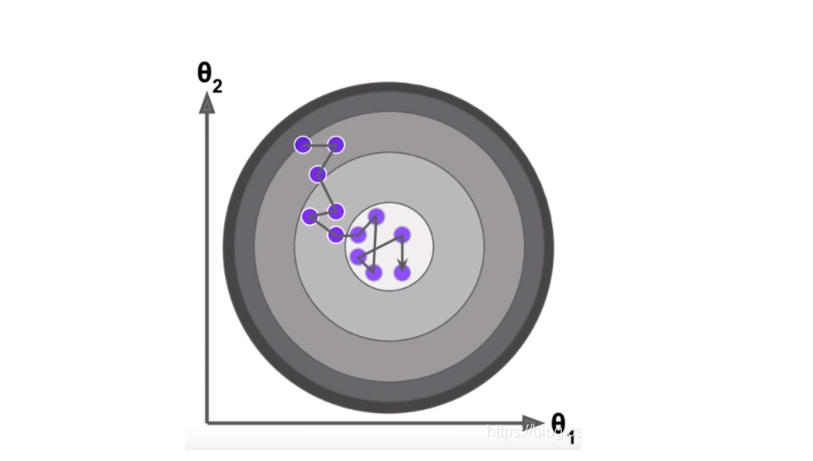
在随机梯度下降法中，学习率的取值很重要。如果我们已经来到了最小值中心的位置了，但是随机的过程不够好，如果学习率是一个固定值的话，有可能会跳出最小值的区域。同时为了避免刚开始的时候梯度下降速度太快，我们通常这样计算学习率:$\eta =\frac{a}{i_{iters}+b}$.
a、b为超参数，通常取a=5,b=50。

5、所有代码实现：

import numpy as np
from sklearn.metrics import r2_score


class LinearRegression:
    def __init(self):
        self.coef_ = None  # 系数
        self.interception_ = None  # 截距
        self._theta = None

    def fit_normal(self, X_train, y_train):
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])  # 构造X_b X_train加上 虚构的都等于1的列
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)  # 通过正规方程解求得theta

        # 分开保存
        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self

    def fit_sgd(self, X_train, y_train, n_iters=5, t0=5, t1=50):

        def dJ_sgd(theta, X_b_i, y_i):
            return X_b_i * (X_b_i.dot(theta) - y_i) * 2.

        def sgd(X_b, y, initial_theta, n_iters, t0, t1):
            # 学习率函数
            def learning_rate(t):
                return t0 / (t + t1)

            theta = initial_theta
            m = len(X_b) #整个样本数
            for cur_iter in range(n_iters): #外层循环代表要看几轮
                indexes = np.random.permutation(m) #对索引进行洗牌操作
                for i,rand_i in enumerate(indexes): # i 代表这一轮中第几次遍历， rand_i是随机索引
                    gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
                    theta = theta - learning_rate(cur_iter * m + i) * gradient  # 每次的随机率都是递减的,cur_iter从0开始，现在要这么计算了
            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.random.randn(X_b.shape[1])
        self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)

        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
        '''
        使用梯度下降法进行训练
        '''

        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
            except:
                return float('inf')

        def dJ(theta, X_b, y):
            return X_b.T.dot(X_b.dot(theta) - y) * 2.0 / len(y)

        def gradient_descent(X_b, y, initial_theta, eta, epsilon=1e-8, n_iters=1e4):
            theta = initial_theta
            i_iter = 0

            while i_iter < n_iters:  # 限定迭代次数
                gradient = dJ(theta, X_b, y)  # 先求出梯度
                last_theta = theta  # 保存之前的theta
                theta = theta - eta * gradient  # 向梯度反方向移动 eta * gradient 这么多
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break
                i_iter += 1
            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])  # 先构造我们的X_b
        initial_theta = np.zeros(X_b.shape[1])  # theta是个向量
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters=n_iters)

        # 分开保存
        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self

    def predict(self, X_predict):
        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression(coef_=%s,interception_=%s)" % (self.coef_, self.interception_)

来源：机器学习入门

最后

以上就是个性手机为你收集整理的线性回归-梯度下降法的全部内容，希望文章能够帮你解决线性回归-梯度下降法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。