多元线性回归实现梯度下降

笔记：


代码实现：

在线性回归模型中使用梯度下降法

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)#数据随机，保持一致
x = 2 * np.random.random(size=100)#100个样本，每个样本有一个特征
y = x * 3. + 4. + np.random.normal(size=100)#均值为0，方差为1

X = x.reshape(-1, 1)#100行，一列数据

X[:20]

array([[ 1.40087424],
       [ 1.68837329],
       [ 1.35302867],
       [ 1.45571611],
       [ 1.90291591],
       [ 0.02540639],
       [ 0.8271754 ],
       [ 0.09762559],
       [ 0.19985712],
       [ 1.01613261],
       [ 0.40049508],
       [ 1.48830834],
       [ 0.38578401],
       [ 1.4016895 ],
       [ 0.58645621],
       [ 1.54895891],
       [ 0.01021768],
       [ 0.22571531],
       [ 0.22190734],
       [ 0.49533646]])

y[:20]

array([ 8.91412688,  8.89446981,  8.85921604,  9.04490343,  8.75831915,
        4.01914255,  6.84103696,  4.81582242,  3.68561238,  6.46344854,
        4.61756153,  8.45774339,  3.21438541,  7.98486624,  4.18885101,
        8.46060979,  4.29706975,  4.06803046,  3.58490782,  7.0558176 ])

plt.scatter(x, y)
plt.show()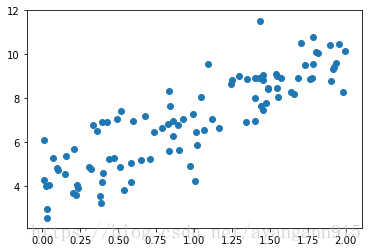

使用梯度下降法训练

#定义损失函数
def J(theta, X_b, y):
    #异常处理，防止溢出
    try:
        return np.sum((y - X_b.dot(theta))**2) / len(X_b)#除以样本数（多少行）
    except:
        return float('inf')

#求导
def dJ(theta, X_b, y):
    res = np.empty(len(theta))#，开一个空间，求导之后结果的长度和x里的元素数目相同
    res[0] = np.sum(X_b.dot(theta) - y)#第0项
    for i in range(1, len(theta)):
        res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])#第i个特征对应的向量即第i列
    return res * 2 / len(X_b)#乘以系数，2/m

#梯度下降过程
def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon=1e-8):

    theta = initial_theta
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta * gradient
        if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
            break

        cur_iter += 1

    return theta

X_b = np.hstack([np.ones((len(x), 1)), x.reshape(-1,1)])#为原先的x添加一列
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01

theta = gradient_descent(X_b, y, initial_theta, eta)

theta

array([ 4.02145786,  3.00706277])

封装我们的线性回归算法

实现：

import numpy as np
from .metrics import r2_score

class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], 
            "the size of X_train must be equal to the size of y_train"

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
        """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], 
            "the size of X_train must be equal to the size of y_train"

        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
            except:
                return float('inf')

        def dJ(theta, X_b, y):
            res = np.empty(len(theta))
            res[0] = np.sum(X_b.dot(theta) - y)
            for i in range(1, len(theta)):
                res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
            return res * 2 / len(X_b)

        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

            theta = initial_theta
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break

                cur_iter += 1

            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, 
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), 
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

from play.LinearRegression import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit_gd(X, y)

LinearRegression()

lin_reg.coef_#系数

array([ 3.00706277])

lin_reg.intercept_#截距

4.021457858204859

最后

以上就是故意小猫咪为你收集整理的多元线性回归实现梯度下降的全部内容，希望文章能够帮你解决多元线性回归实现梯度下降所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。