线性回归模型表达式:
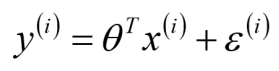
- 其中theta.shape=(1,m),m=数据的特征数量。
- 通过直接求导,可以得到theta的最优解,但是会遇到矩阵求逆的问题,而并不是所有的矩阵都可以求逆。
- 由于矩阵求逆的不确定性,因而想到了用梯度下降法来逐步逼近最优解,梯度下降法又分为BGD、SGD、MBGD。
- BGD每次更新需要用全部数据,计算量大且耗时;SGD每次更新需要用一条数据,计算量小速度快,但是可能在最小值附近波动,不收敛;MBGD每次更新用一部分数据(batch_size),计算速度并不会比SGD慢太多,每次使用一个batch_size可以大大减小收敛所需要的迭代次数。
- batch_size根据GPU来选择,一般是32的倍数。
#coding=utf-8
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
np.random.seed(4)
class LR:
def __init__(self,iter_n=30,learn_rate=0.001,batch_size=2):
self.iter_n = iter_n
self.learn_rate = learn_rate
self.batch_size = batch_size
#线性回归算法模型:theta*x
def model(self,x,theta):
return np.dot(x,theta)
#损失函数(目标函数):选用MSE均方误差
def mse(self,y,y_hat):
return sum((y-y_hat)**2)/len(y)
#计算梯度
def cal_gred(self,y,y_hat,x):
#初始化梯度
gred = np.zeros((x.shape[-1],1))
#计算每个theta的梯度
for index in range(len(gred)):
gred[index][0] = sum((y-y_hat)*x[:,index:index+1]) #损失通过推倒发现是最小二乘法表达式,再求导就是这个式子
return gred
#打乱数据
def shuffle(self,x,y,y_hat):
all_data = np.hstack((x,y,y_hat))
print(all_data)
np.random.shuffle(all_data)
return all_data[:,:x.shape[-1]],all_data[:,x.shape[-1]:x.shape[-1]+1],all_data[:,-1:]
#画损失曲线
def draw_loss(self,count,loss):
plt.plot(range(count+1),loss,color='r',marker='o')
plt.show()
#对新数据预测
def predict(self,x):
x.insert(0,1)
x = np.array(x)
y_pre = self.model(x,self.theta)
#print(y_pre)
return y_pre
#拟合
def fit(self,x,y):
#训练数据增加一列1,因为theta有偏置项
x_ones = np.ones((len(x),1))
x = np.hstack((x_ones,x))
#初始化theta,初始值设为0
theta = np.zeros((x.shape[-1],1)) #theta.shape=(4,1)
#计算预测值(第一次)
y_hat = self.model(x,theta)
#计算损失(第一次)
loss = []
loss.append(self.mse(y,y_hat))
#记录迭代次数
count = 0
while True:
#训练一轮(epoh)数据
for n in range(int(len(x)/self.batch_size)):
gred = self.cal_gred(y[n*self.batch_size:(n+1)*self.batch_size],y_hat[n*self.batch_size:(n+1)*self.batch_size],x[n*self.batch_size:(n+1)*self.batch_size])
theta = theta+self.learn_rate*gred
y_hat = self.model(x,theta)
loss.append(self.mse(y,y_hat))
count += 1
#停止条件 方式1 (用迭代次数控制)
if count >= self.iter_n:
#print(f'停止条件为方式1,迭代次数count={count}')
break
#停止条件 方式2 (用损失不再降低来控制)
if loss[-2]-loss[-1] < 1e-5:
#print(f'停止条件为方式2,迭代次数count={count}')
break
#一轮数据全部使用完后,打乱
x,y,y_hat = self.shuffle(x,y,y_hat)
self.draw_loss(count,loss)
self.theta = theta
if __name__=='__main__':
train_data = pd.read_excel('lr.xlsx',sheet_name='训练数据') #train_data.shape=(10,4)
train_data_x = np.array(train_data.iloc[:,:-1]) #train_data_x.shape=(10,3)
train_data_y = np.array(train_data.iloc[:,-1:]) #train_data_y.shape=(10,1)
#手写代码结果
print('------手写结果:以下是手写的线性回归模型结果------')
lr1 = LR(iter_n=30, learn_rate=0.001, batch_size=4)
lr1.fit(train_data_x, train_data_y)
print('预测值为:',lr1.predict([2,4,3])) #根据拟合的模型,对数据[2,4,3]进行预测,y_hat=1.76261384
print('截距+权重:',lr1.theta.T) # y = theta0*1 + theta1*x1 + theta2*x2 + theta3*x3
# [[theta0 theta1 theta2 theta3]] = [[0.03055664 0.24267117 0.15796392 0.20495306]]
#调包结果
print('------调包结果:以下调用sklearn中线性回归模型结果------')
lr2 = linear_model.LinearRegression()
lr2.fit(train_data_x, train_data_y) # y = intercept_ + theta1*x1 + theta2*x2 + theta3*x3
print('预测值为:',lr2.predict(np.array([[2,4,3]]))) #根据拟合的模型,对数据[2,4,3]进行预测,y_hat=1.62696405
print('权重:',lr2.coef_) # 特征前的系数(权重):[[theta1 theta2 theta3]] = [[0.19642699 0.35235242 0.31708833]]
print('截距:',lr2.intercept_) # 截距:[intercept_] = [-1.12656458]
注:lr.xlsx数据是随便写的,不具有参考价值
| x1 | x2 | x3 | y |
|---|---|---|---|
| 2 | 4 | 3 | 1.3 |
| 3 | 4 | 3 | 2.3 |
| 4 | 5 | 6 | 3.4 |
| 5 | 5 | 0 | 2.1 |
| 6 | 4 | 3 | 1 |
| 7 | 4 | 7 | 5 |
| 8 | 3 | 7 | 4.5 |
| 9 | 4 | 7 | 3 |
| 10 | 7 | 7 | 4 |
| 11 | 7 | 6 | 7 |
最后
以上就是敏感犀牛最近收集整理的关于机器学习算法:线性回归 - MBGD小批量梯度下降法 - 手写代码的全部内容,更多相关机器学习算法:线性回归内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复