【机器学习】【RNN中的梯度消失与梯度爆炸】

学习speech synthesis的Tacotron模型，而Tacotron是基于seq2seq attention，RNN中的一类。所以得先学习RNN，以及RNN的变种LSTM和GRU。

RNN的详细我这里不再介绍了，许多神犇的博客及网上免费的课程讲得都很详细。这里仅说明RNN中的梯度消失与梯度爆炸。文章若有错误，烦请大家批评指正。

以经典RNN为例，

假设我们的时间序列只有三段，S0为给定值，则RNN的前向传播过程：

S1=tanh(Wx*X1+Ws*S0+b1)，O1=Wy*S1+b2，y1=g(O1)=g(Wy*S1+b2)

S2=tanh(Wx*X2+Ws*S1+b1)，O2=Wy*S2+b2，y2=g(O2)=g(Wy*S2+b2)

S3=tanh(Wx*X3+Ws*S2+b1)，O3=Wy*S3+b2，y3=g(O3)=g(Wy*S3+b2)

其中Wx为处理输入的参数，Wy为处理输出的参数，Ws为处理前一个时间序列的参数。

假设损失函数为L=1/2*(Y-y)^2，即在t=3时刻，损失函数为L3=1/2*(Y3-y3)^2

对于每一次训练，损失函数为L=∑(t=0,T)Lt，即每一时刻损失值的累加。

我们训练RNN的目的就是不断调整参数，即Wx、Ws、Wy和b1，b2，使得它们让L尽可能达到最小。

假设我们的三段时间序列为t1，t2，t3。

我们考虑t3时刻，对t3时刻的Wx、Ws、Wy求偏导：

可以看出，时间序列对Wy没有长期依赖，而对Wx和Ws的偏导会随着时间序列的增加，中间的求积过程就会不断增加。

因此，根据上面的求偏导公式，可以得到任意时刻对Wx的求偏导公式：

任意时刻对Ws的的求偏导公式和上面类似。

而其中，Sj对Sj-1的偏导数，就是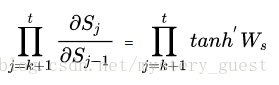

激活函数tanh和它的导数图像如下：（引用自zhihu）

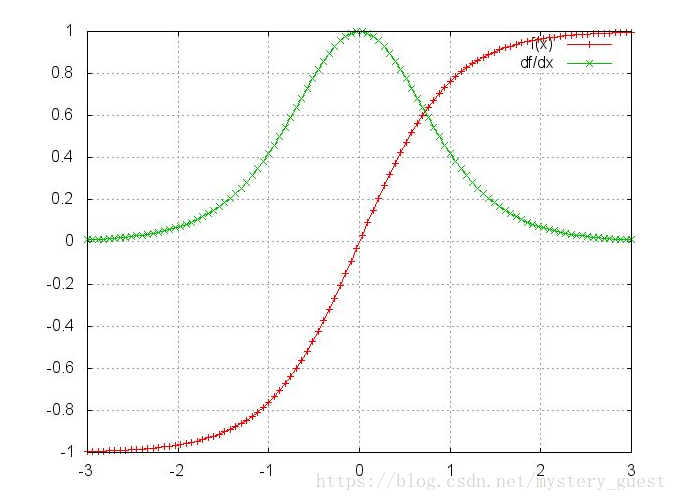
可以看出，激活函数tanh的导数是小于等于1的，训练的过程中大部分情况下也小于1，因为很少出现WxXj+WsSj-1+b1=0的情况。如果Ws是一个大于0小于1的值，那么当t很大时，就会无穷小，即趋于0；当Ws很大时，则会趋于无穷。

因此，梯度消失和梯度爆炸的根本原因就是这一坨连乘，我们要尽量去掉这一坨连乘，一种办法就是使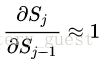另一种办法就是使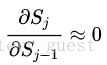其实这就是LSTM做的事情。

最后

以上就是怕孤单指甲油为你收集整理的【机器学习】【RNN中的梯度消失与梯度爆炸】的全部内容，希望文章能够帮你解决【机器学习】【RNN中的梯度消失与梯度爆炸】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。