循环神经网络_基础

处理序列数据：

语言识别、音乐生成、情感分类、机器翻译、视频行为识别、命名实体识别。

前馈神经网络与循环神经网络

前馈神经网络

1. 不考虑上下文信息，输入固定则输出固定；
2. 不同的训练样本，输入、输出序列的长度不同,前馈神经网络不能很好地解决这个问题；
3. 在文本序列不同位置学习到的特征不共享，这指的是比如当人名出现在不同位置，前馈神经网络无法做到一视同仁；

以词汇序列为例，我们想要提取目的地与时间。

1. 将语句转化为向量；
2. 输入Feedforward Network。
3. 输出该词汇属于目的地或时间的概率。

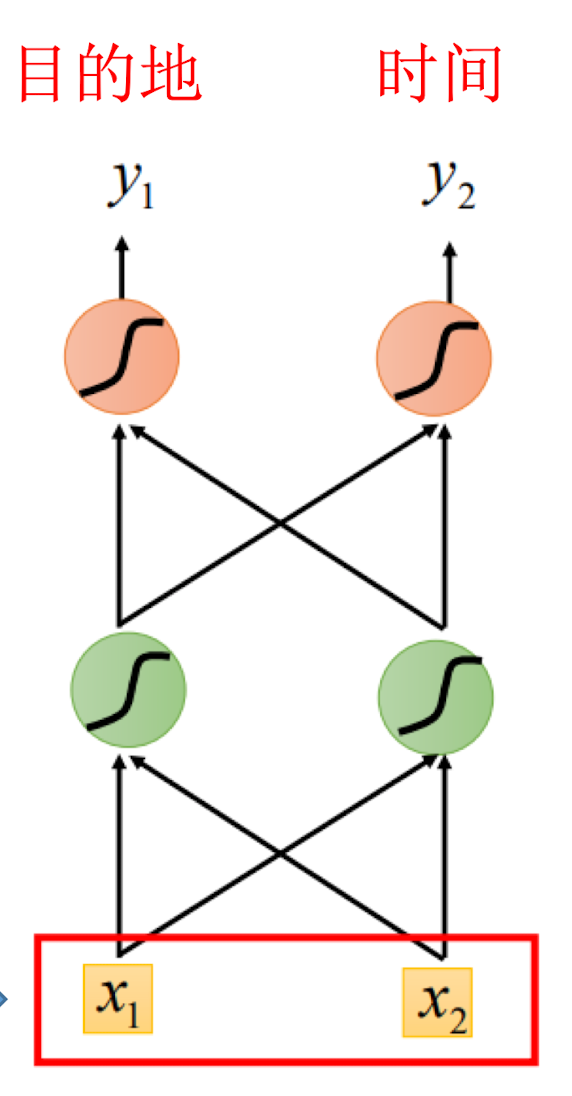
如何用向量表示词汇？

1-of-N encoding：

1. 准备一张词汇表；
2. 对应词汇的位置记录为1；

Beyond 1 of N encoding：
有时会出现词汇表中不出现的词汇，此时为词汇表增添一个other选项，用以表示该类词汇。

循环神经网络——三种简单的RNN

以词汇序列为例，leave for Dalian 和 leave Dalian的意思截然相反，但是Feedforward Netwok无法识别出，因为其不含"记忆"。
神经网络需要记忆功能，捕获历史时刻的信息。

该网络将每一个神经元的输出存到“记忆”中去，当下次再有输入时，一同传导进神经元。起始时，一般将记忆置零。
回顾：

1. 使用自带反馈的神经元，能够处理任意长度的时序数据；
2. 比前馈神经网络更加符合生物神经网络的结构；
3. 网络具有自适应记忆能力。

Elman RNN

我们对于词汇序列的模型测试过程可视化为：

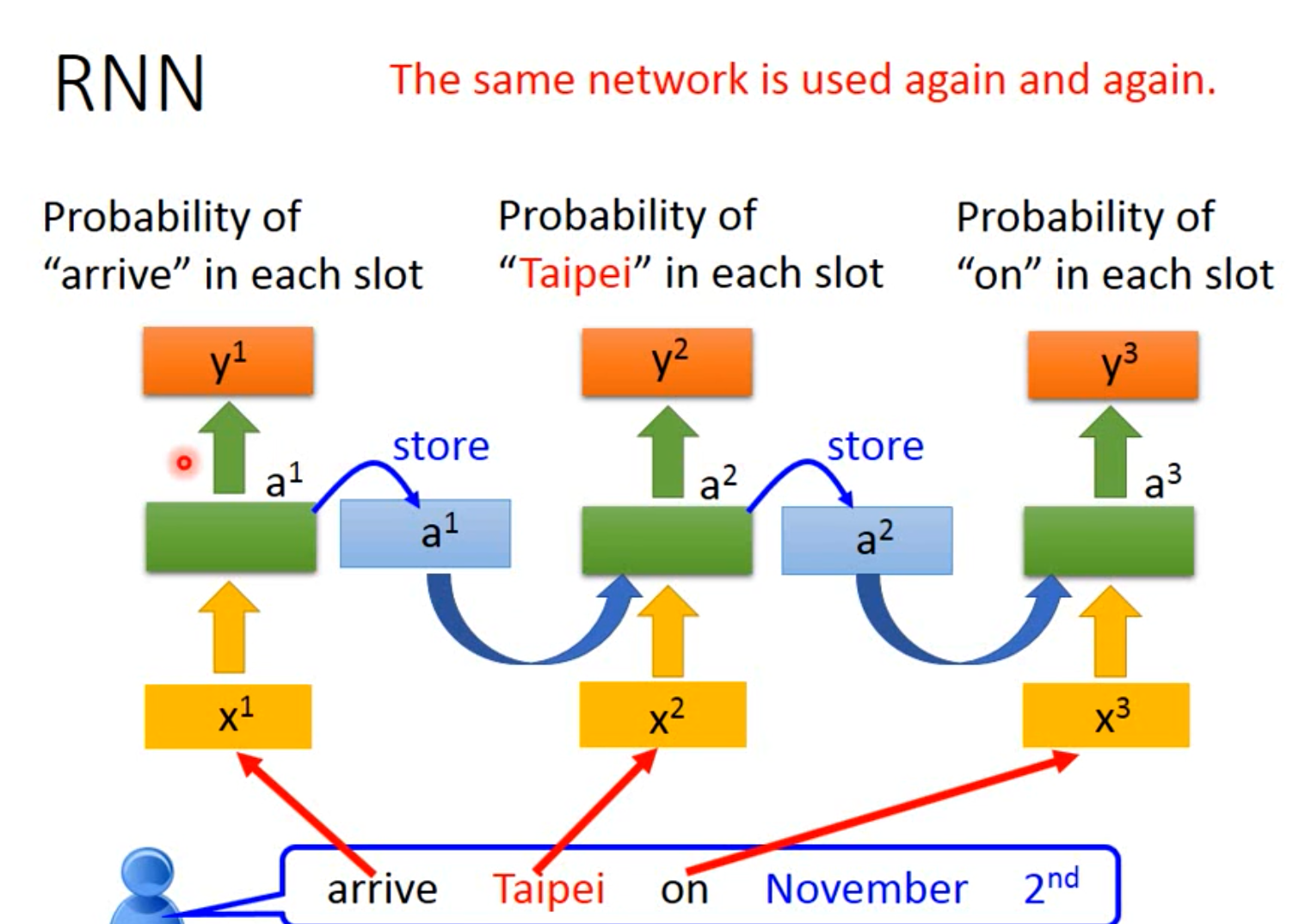
同一个模型执行三次，不是这个模型包含三个层。

以上被称为Elman Network，仅对每一个神经元进行操作；Elman Network 又被称为SRN(Simple Recurrent Network),是在Jordan Network的基础上发展的，其结构具体如下图：

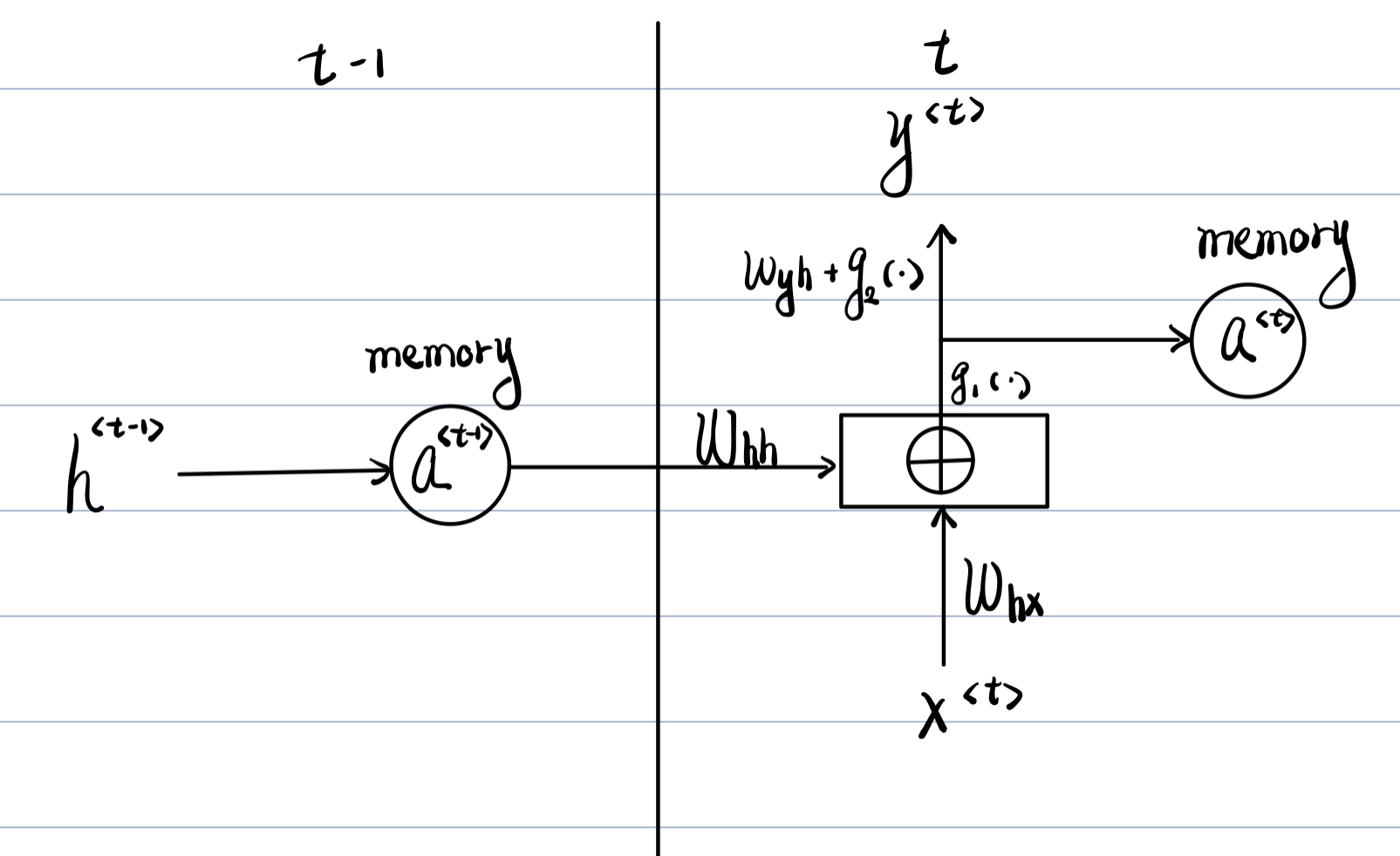
激活函数1为tanh，激活函数2位Softmax。

命名实体识别

识别文本中具有特定意义的实体，比如人名、地名、机构名等。

设定符号：

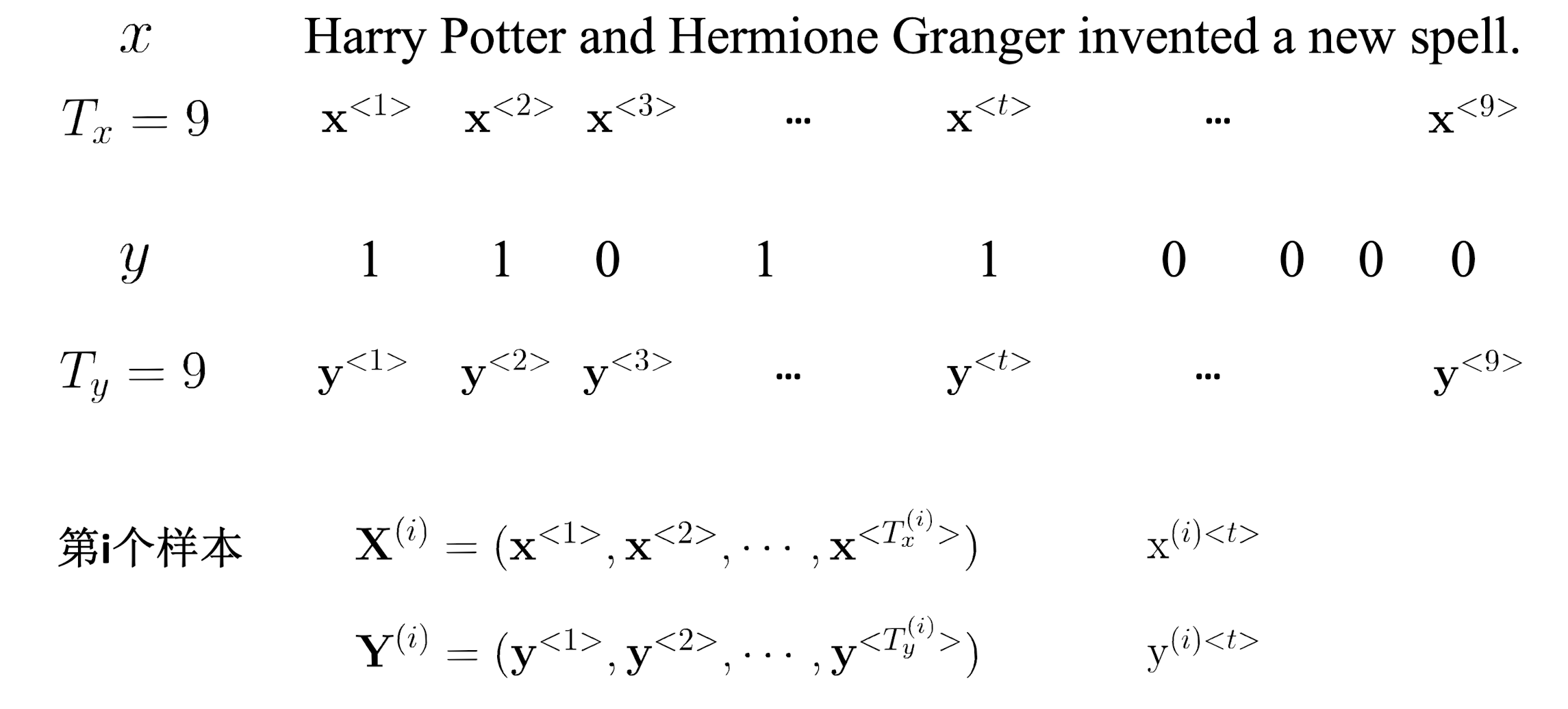
设定词向量：

训练与测试：

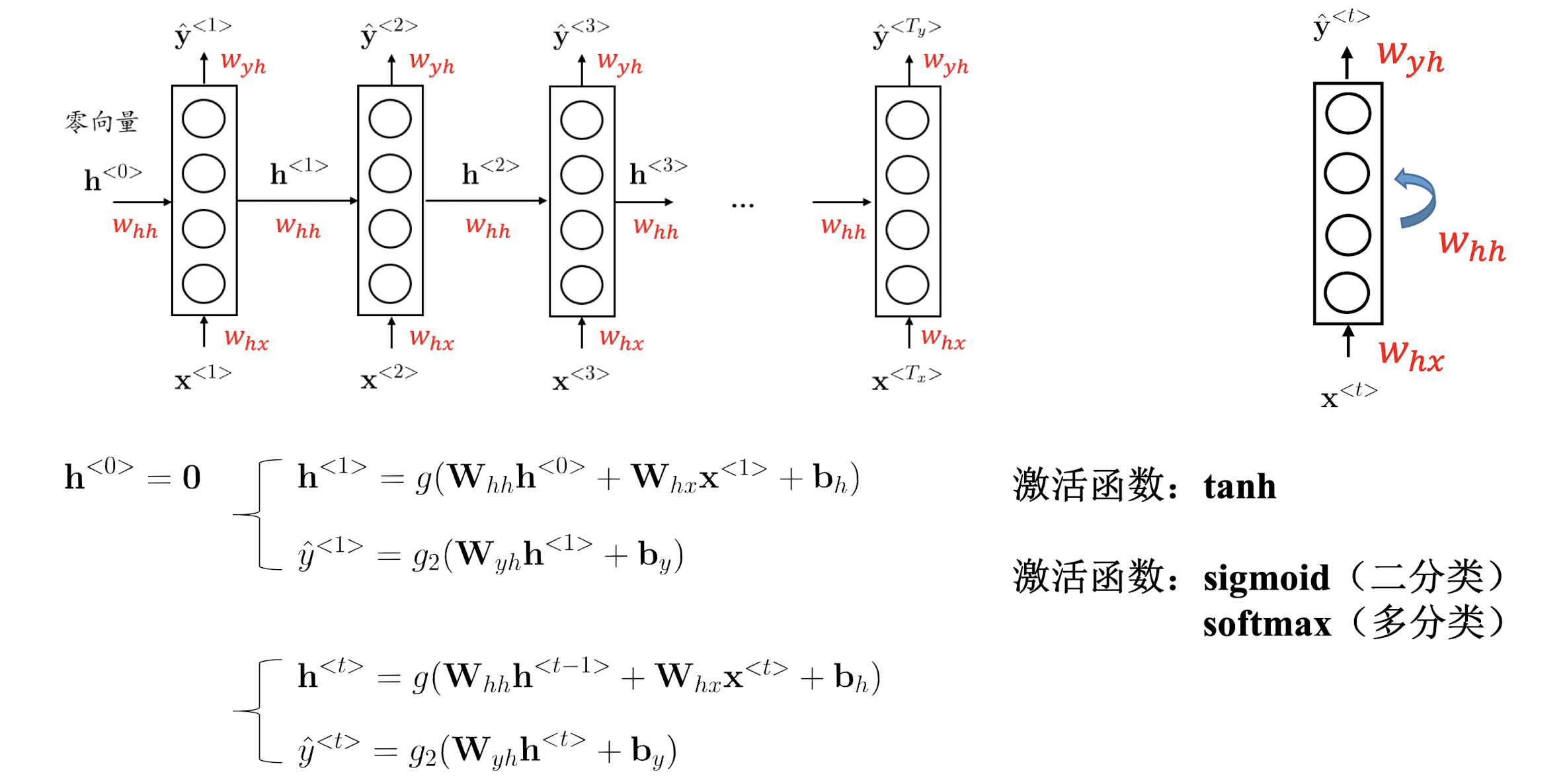
在这样一个问题中，模型从左到右扫描序列数据，每一个时间步都共享参数。
需要注意的是：
隐藏层输出到模型输出，需要进行两次激活函数，且激活函数不一致。

其中，损失函数为BCELoss：

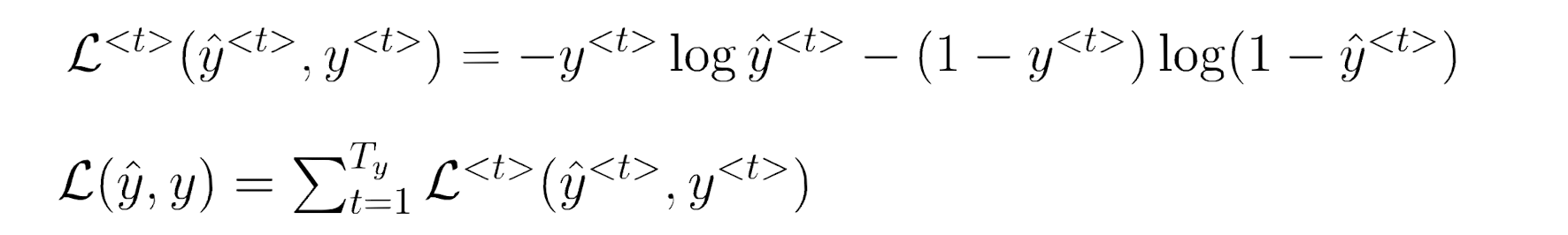
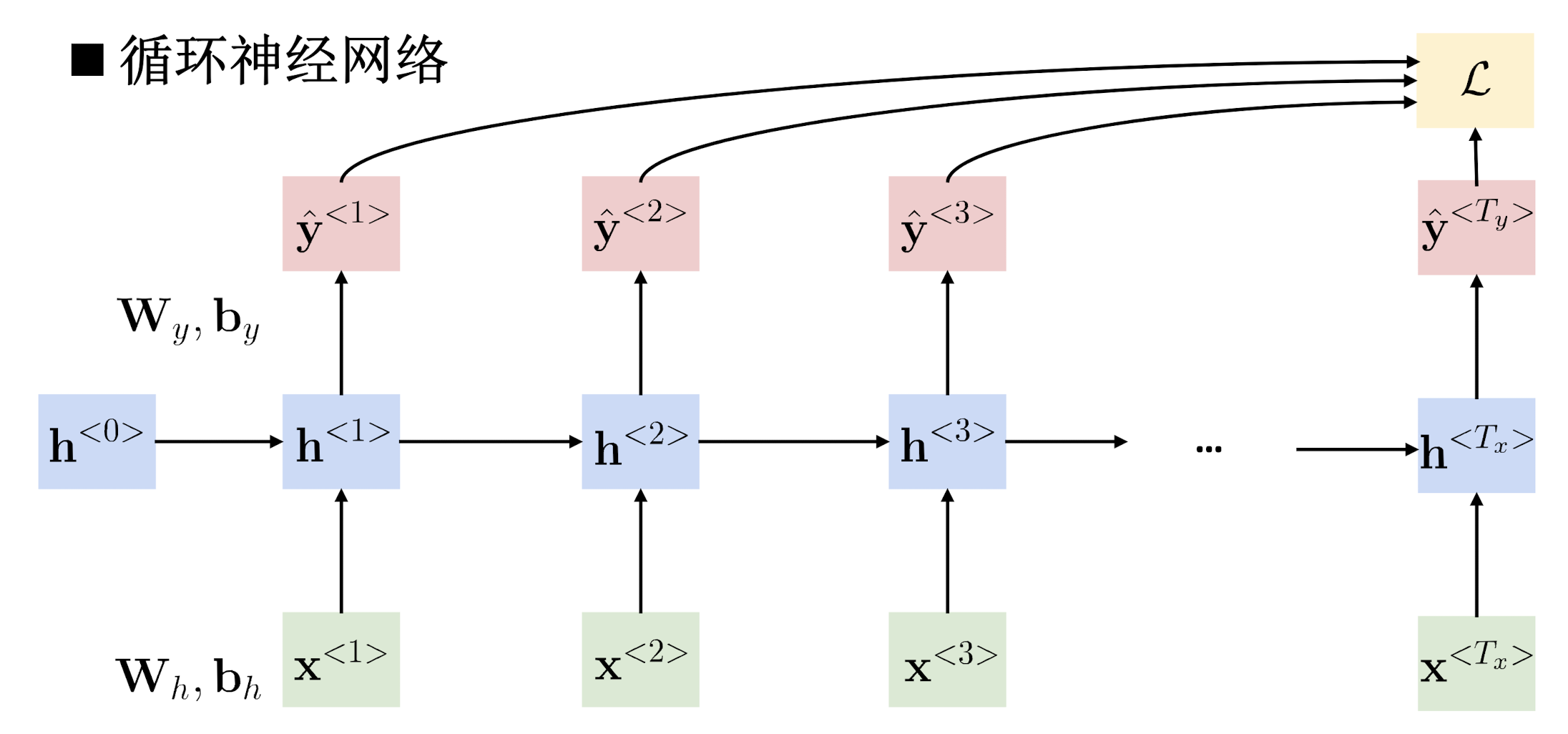
循环神经网络近似定理

Jordan RNN

还有Jordan Network 存储的是模型的输出，对模型整体进行操作。

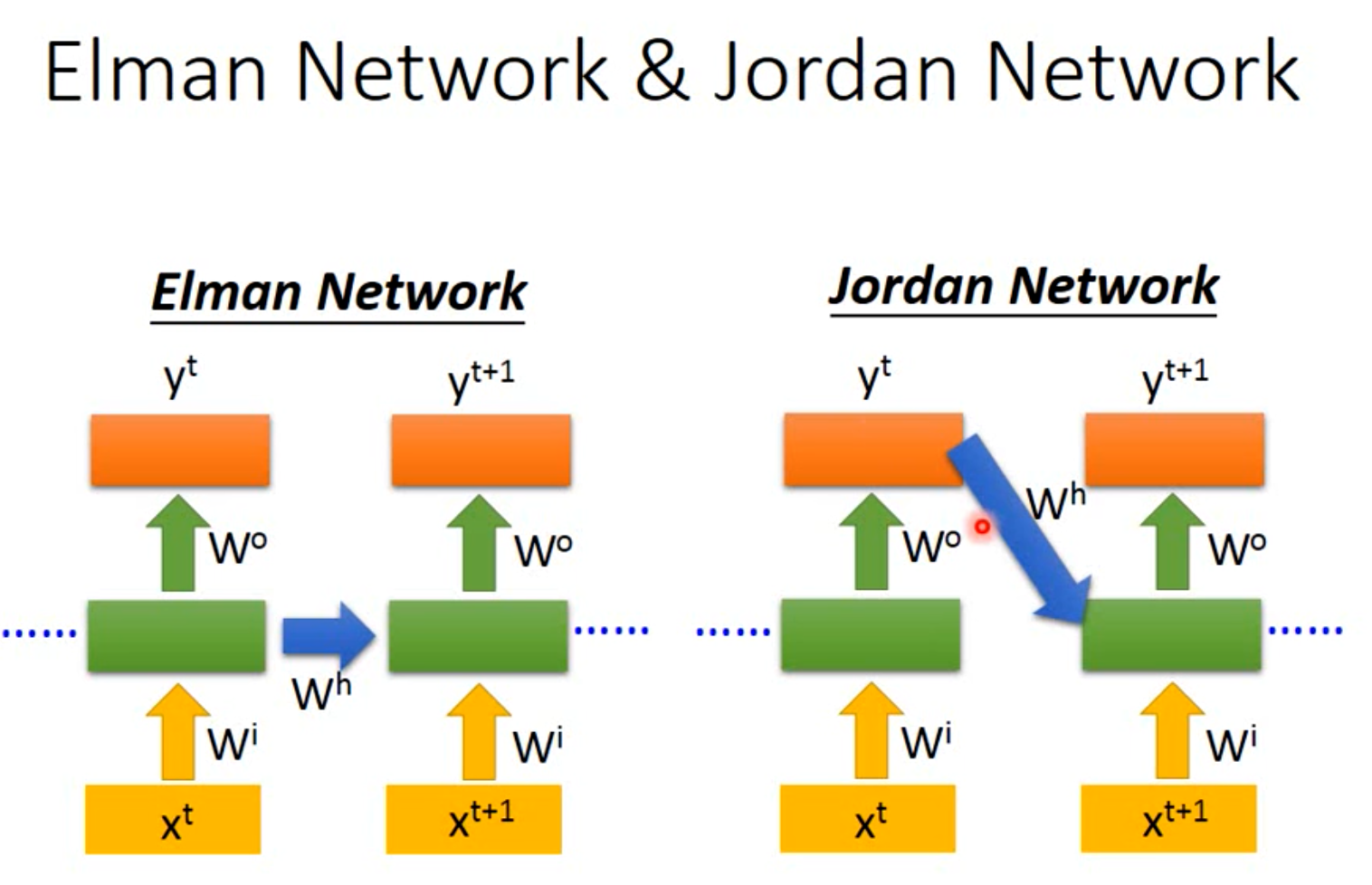
其中，Jordan RNN效果更好。

Bidirectional RNN

双向循环神经网络。

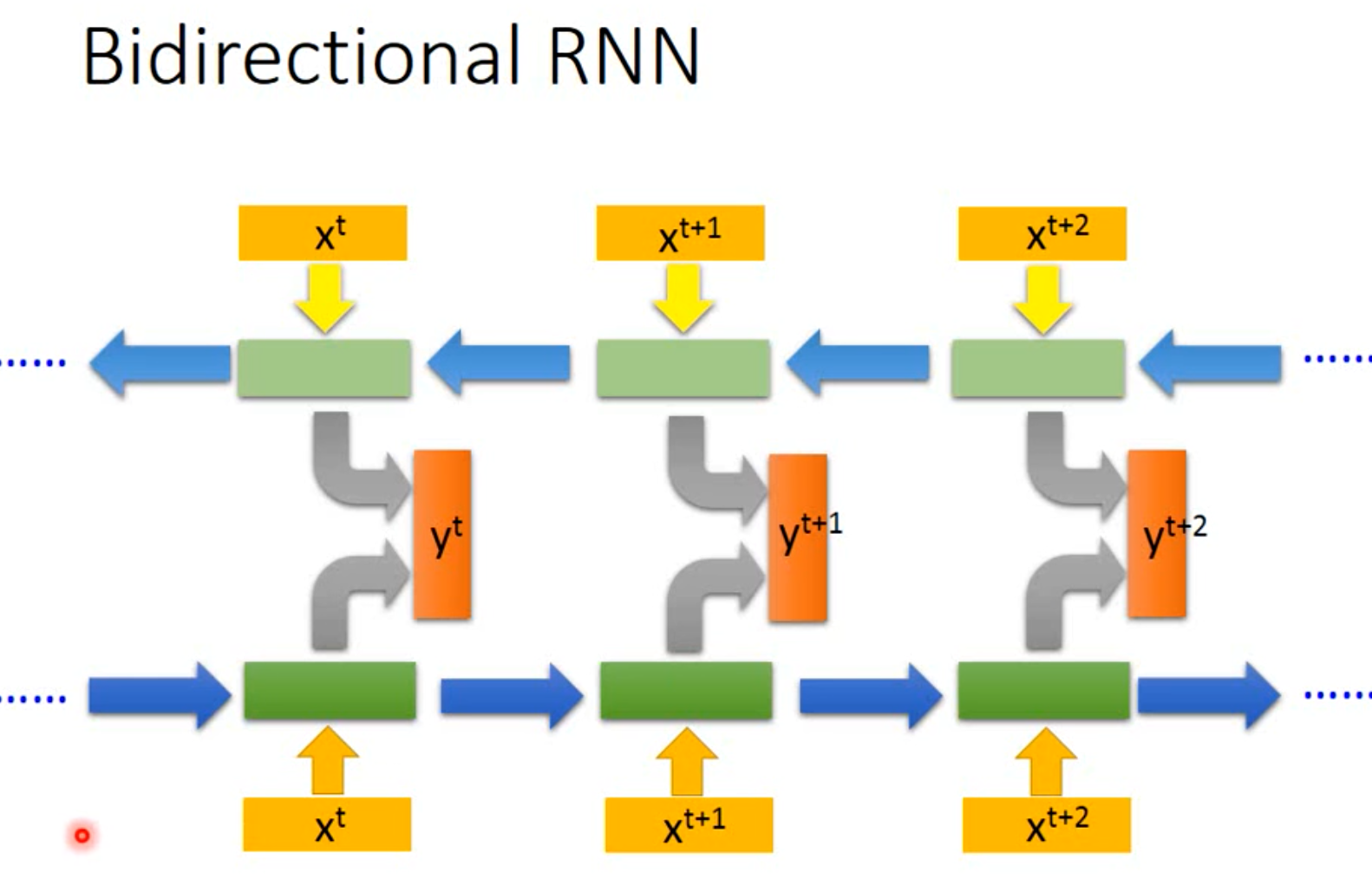
每一个输出，联系了上下文，观测的东西更多。
获取历史数据的信息 + 获取未来数据的信息。
缺点：需要获取完整的序列才能预测，不能实时处理。

不同结构的RNN

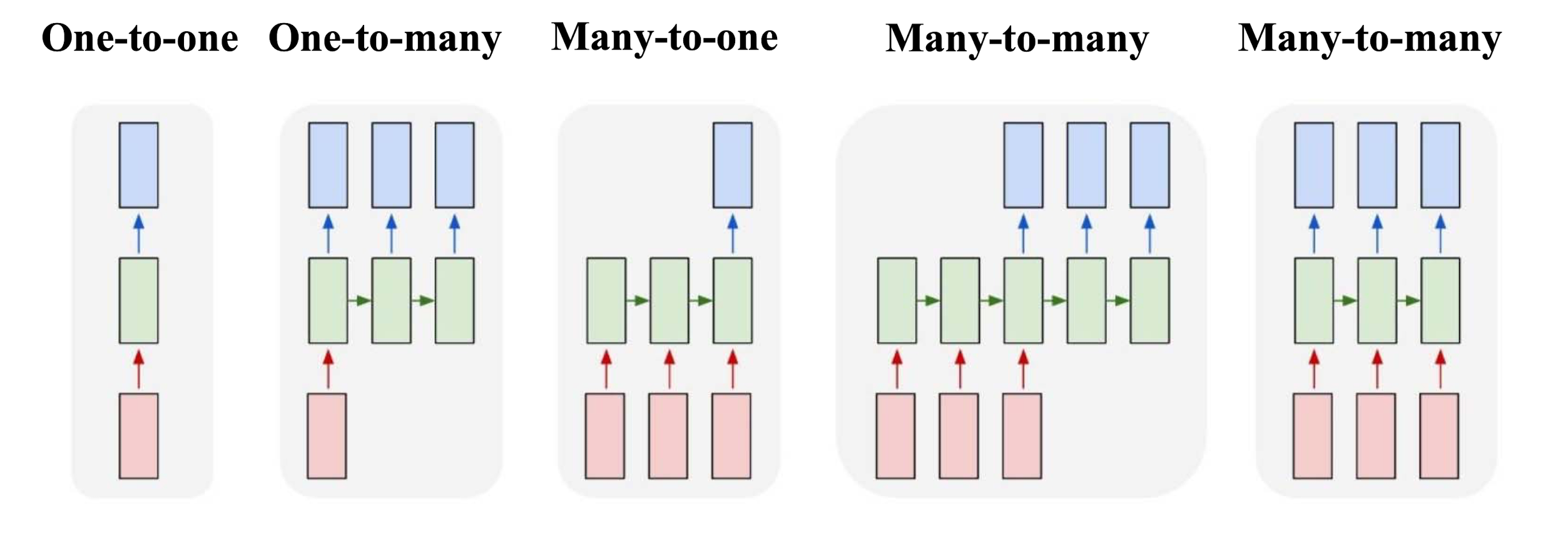
蓝色表示输出，绿色表示隐藏层，红色表示输入。

One to many

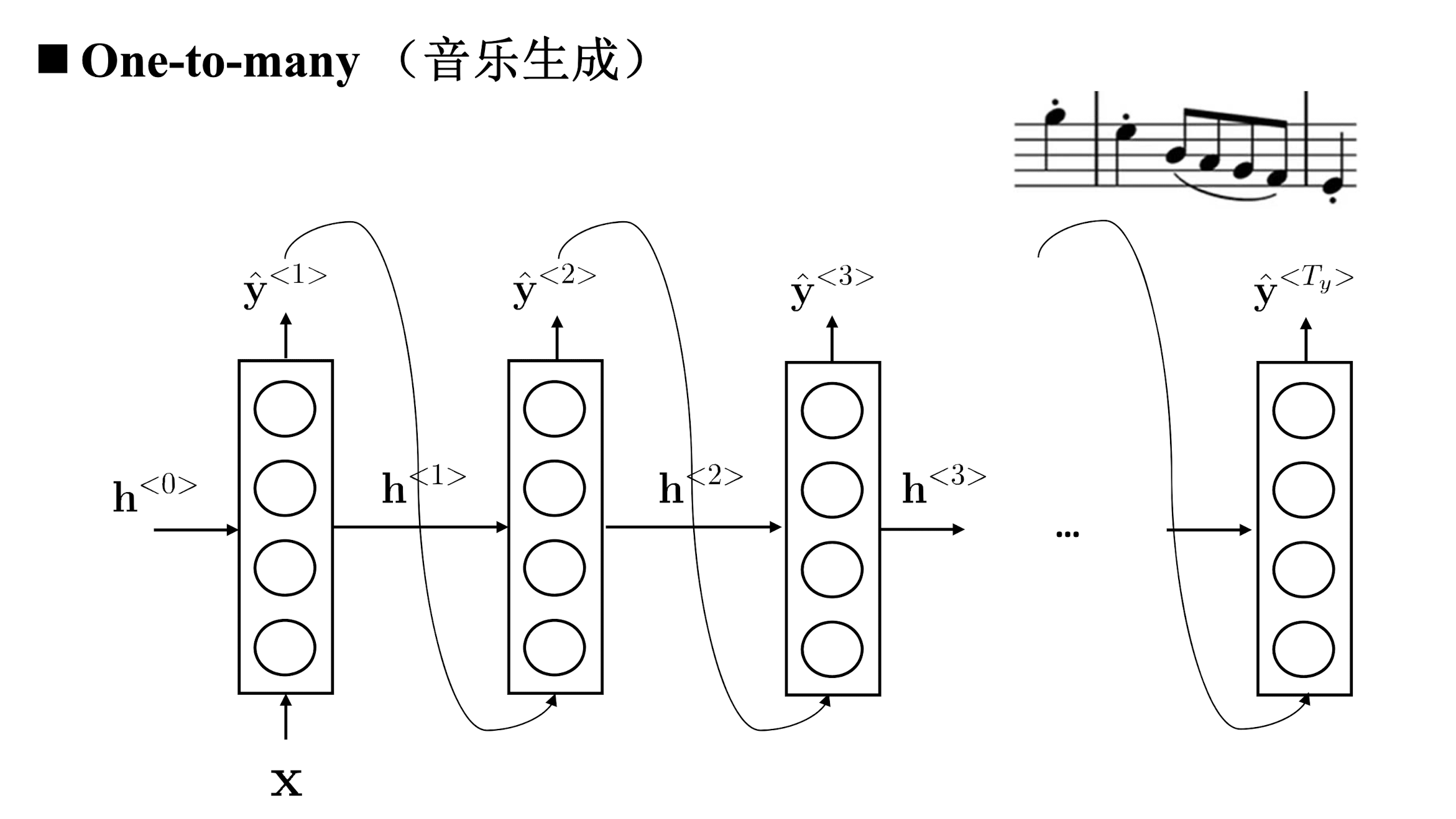
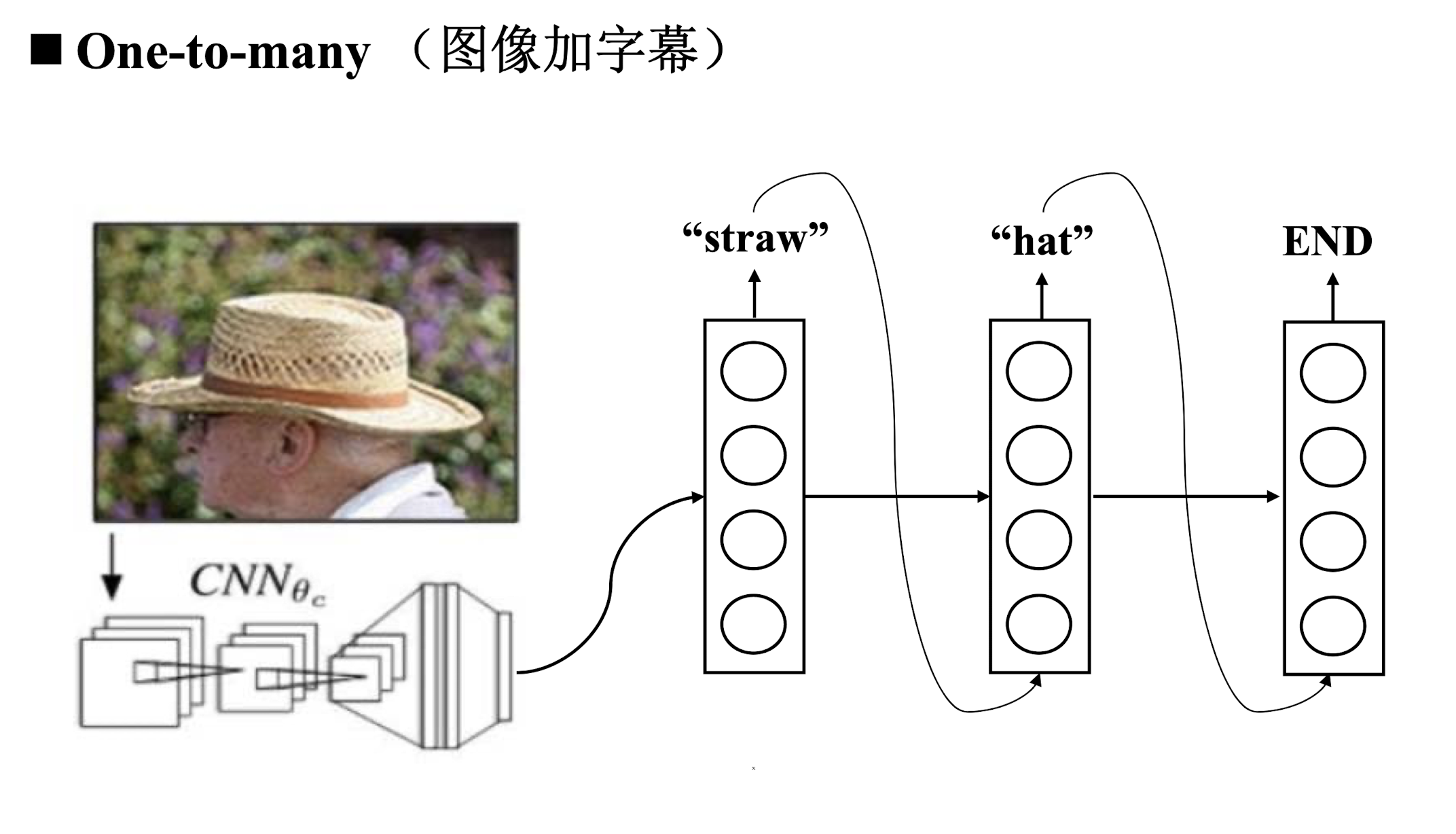
Many to one

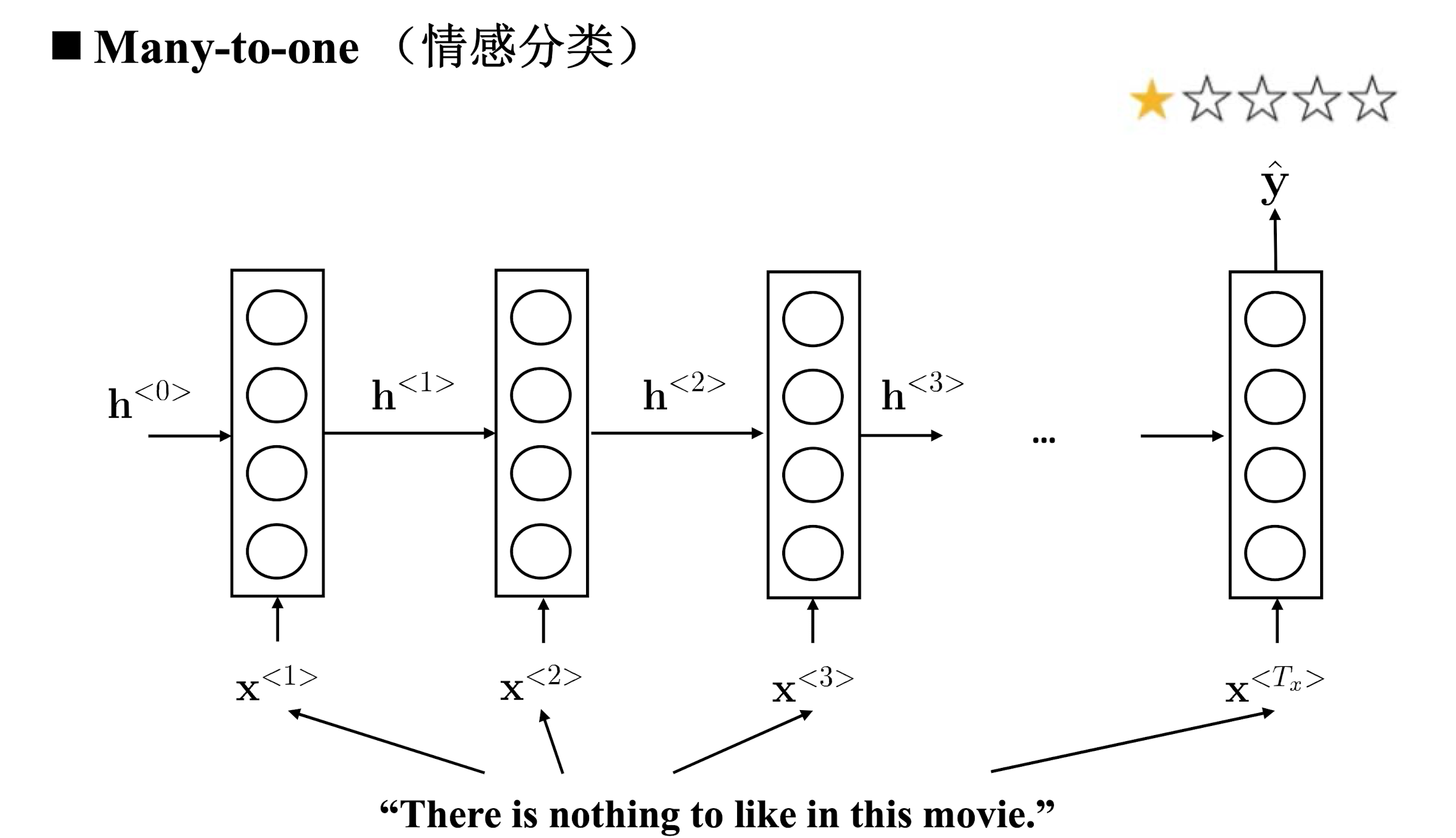
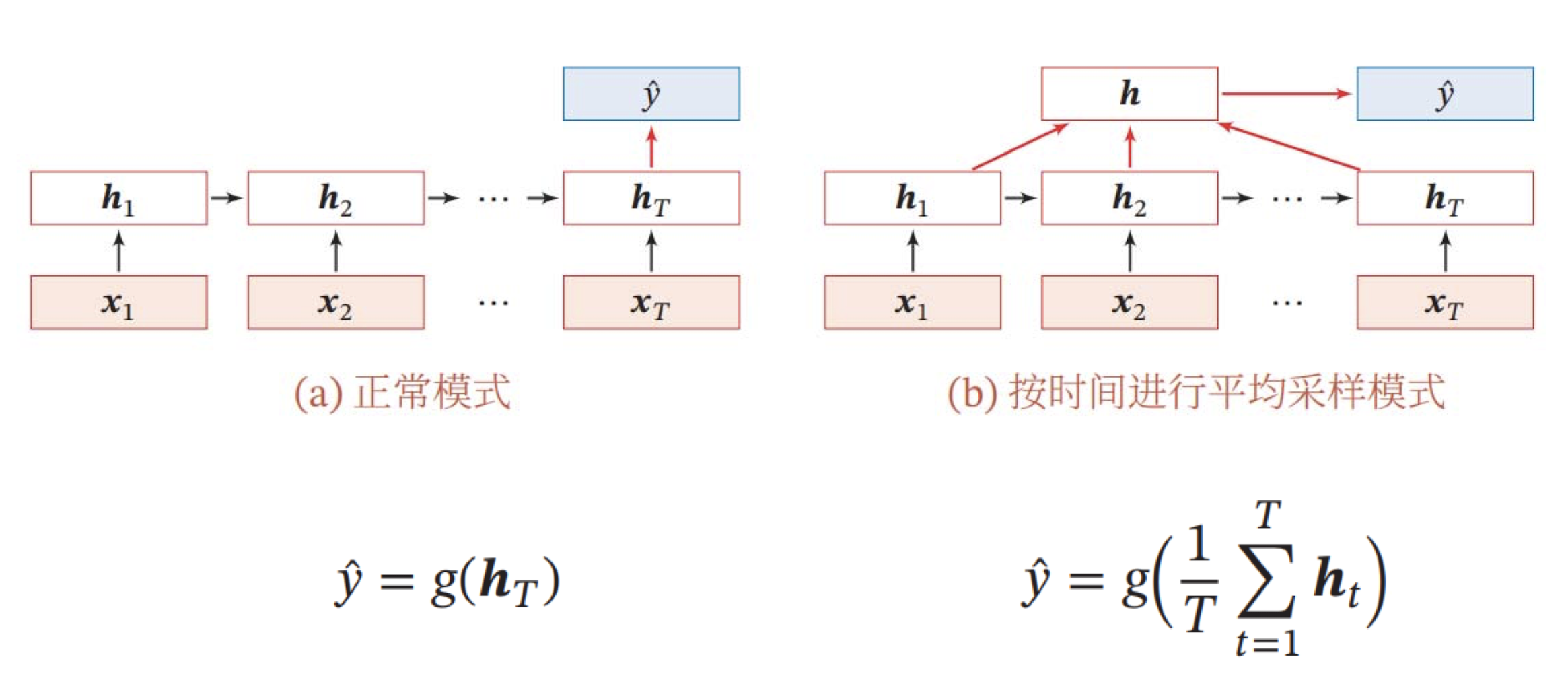
Many to many

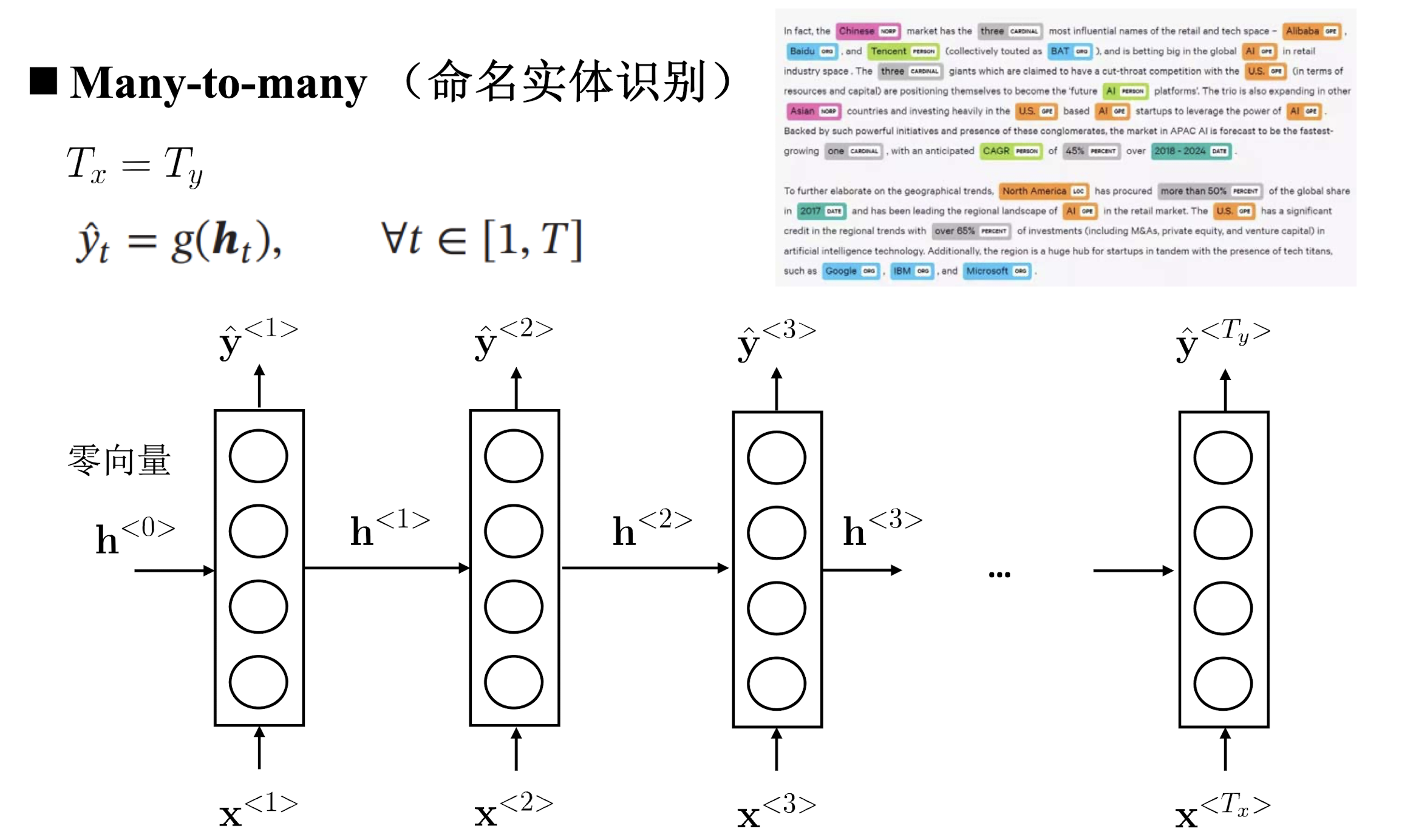
输入输出长度一致。

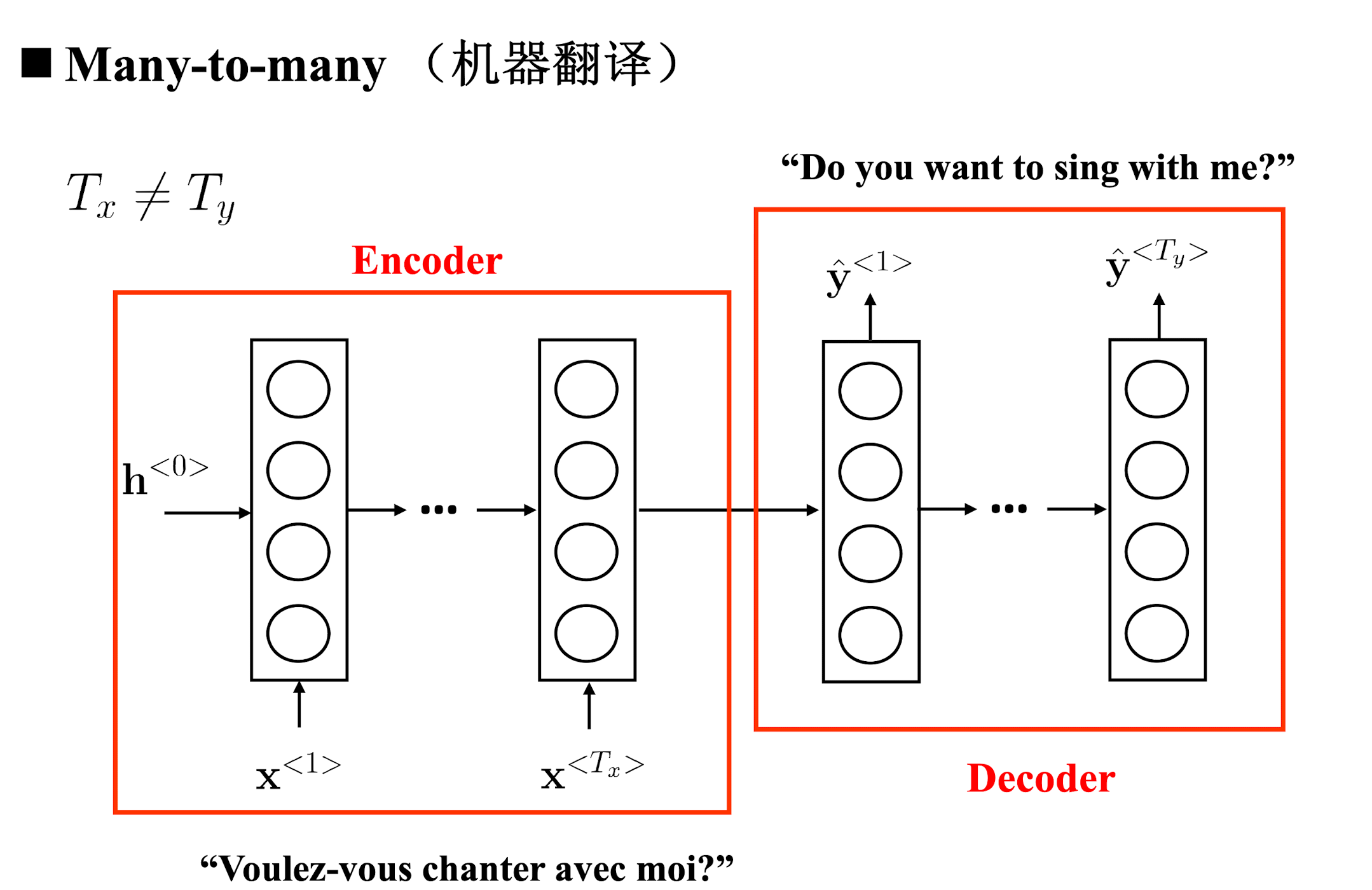
输入输出长度不一致。

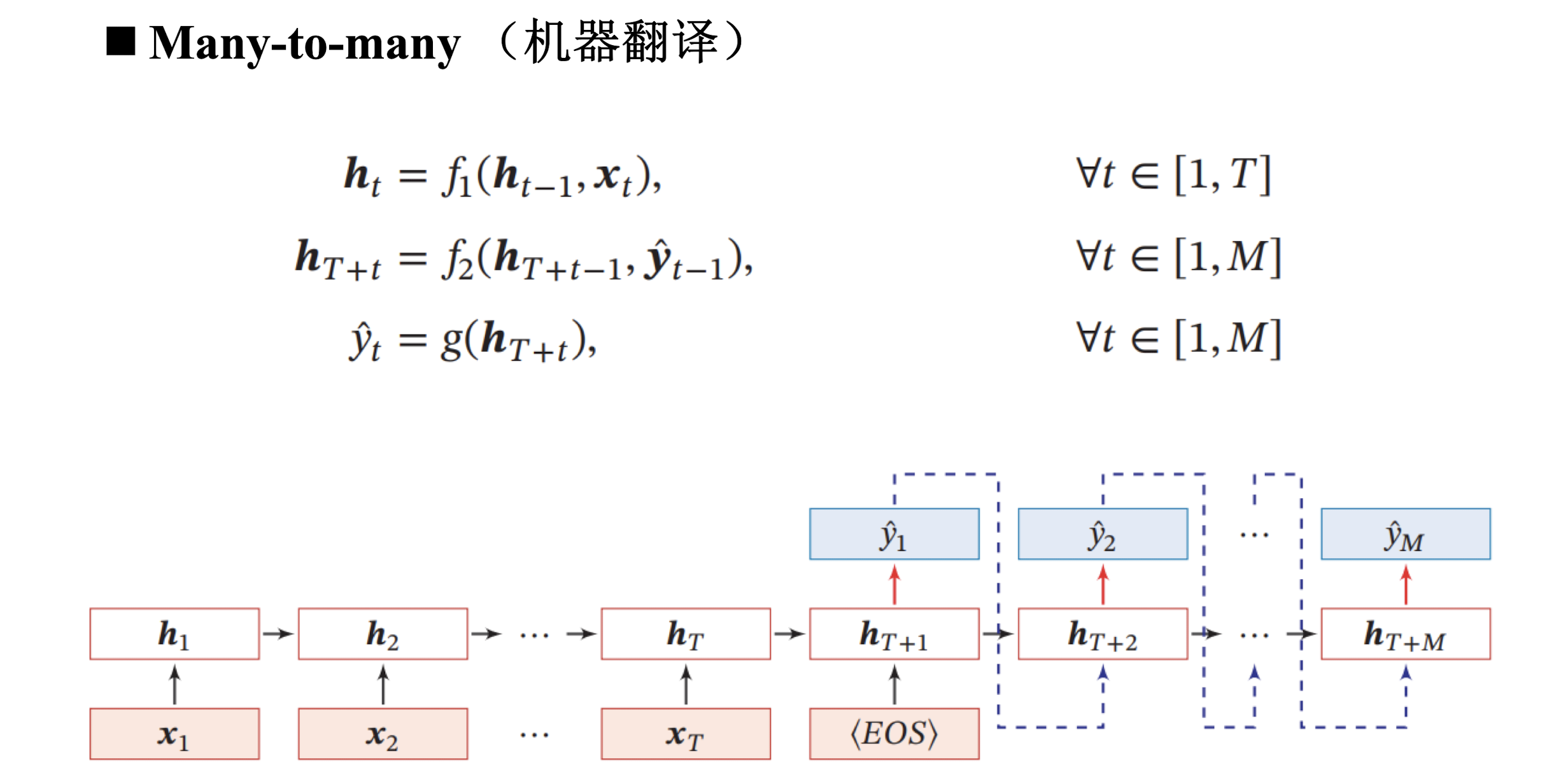
循环神经网络训练

训练很困难；

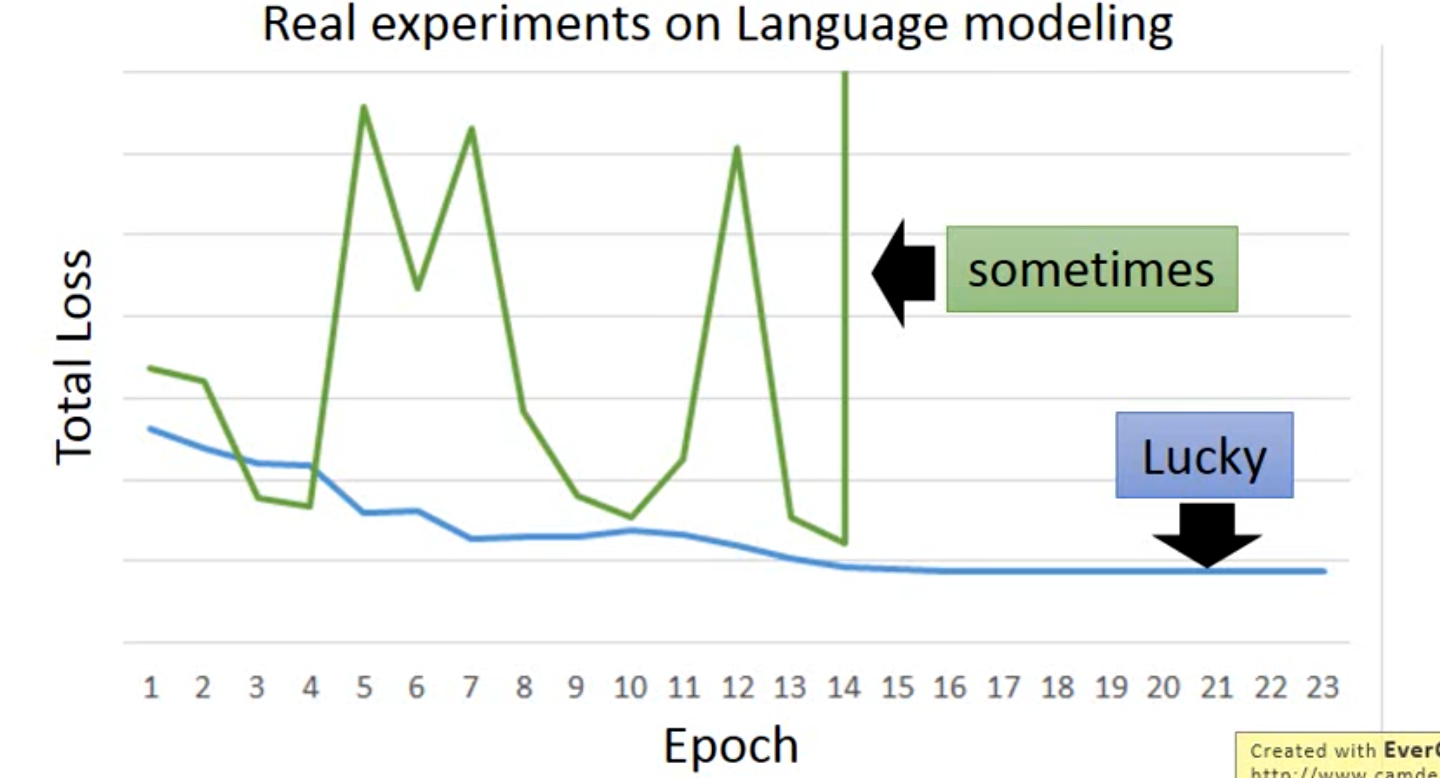
这是因为它的优化平面是很崎岖的，

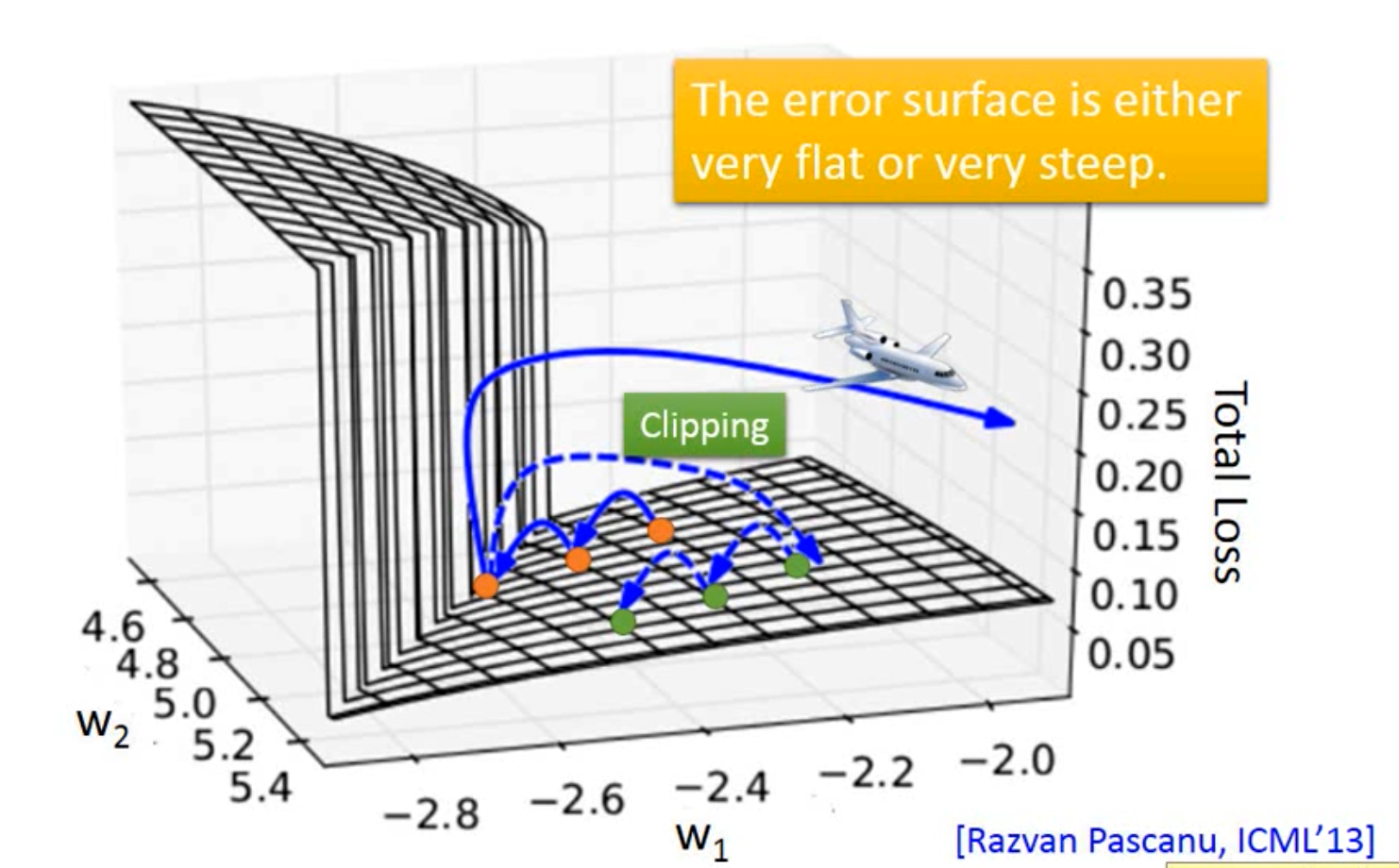
可以采用Clipping解决在崎岖表面学习的问题。

BPTT(Backpropagation through tIme)

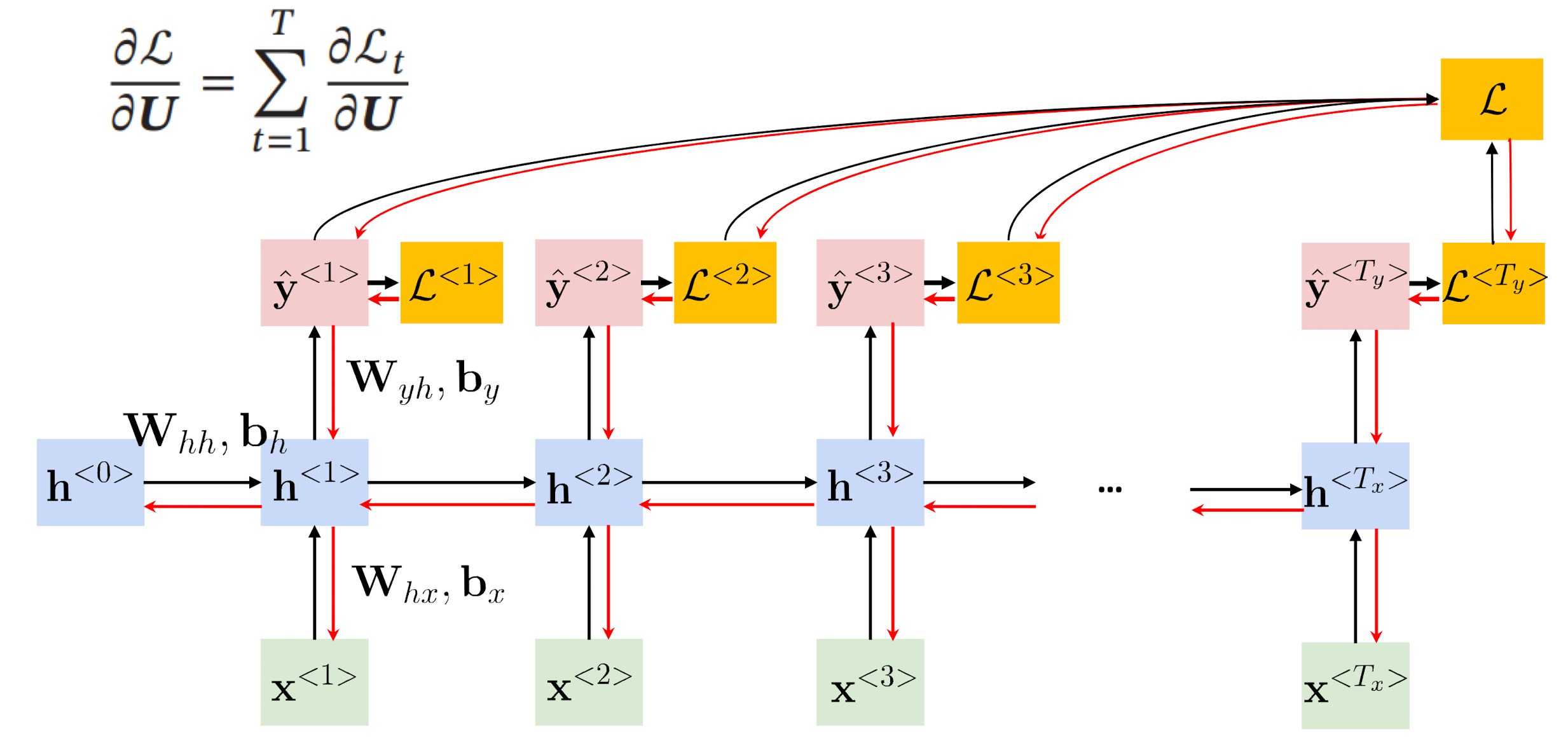
我们以Elman RNN为例
中心思想和BP算法相同，本质是梯度下降法。需要寻优的参数有三个，${\omega }_{hh},{\omega }_{hx},{\omega }_{yh}$。与BP算法不同的是${\omega }_{hh},{\omega }_{hx}$在寻优的过程中，需要追溯之前的历史数据，因此RNN有记忆功能。

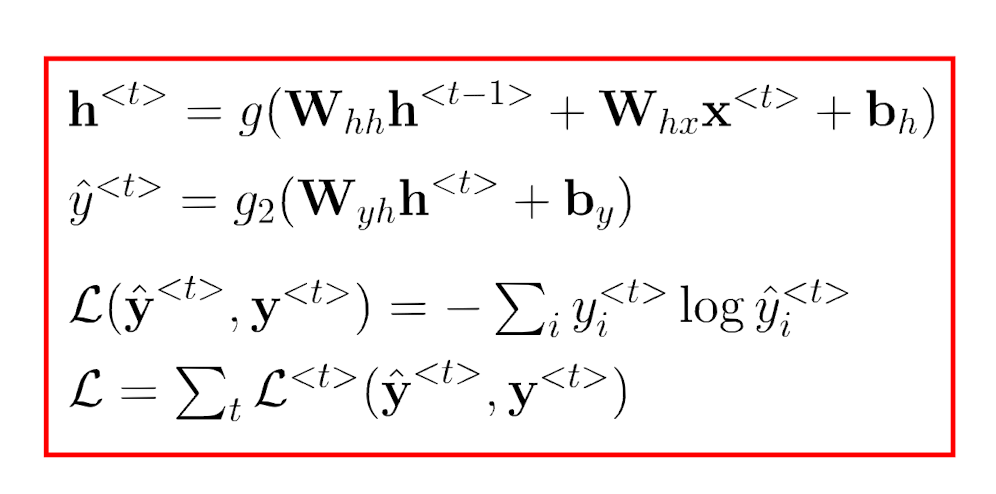
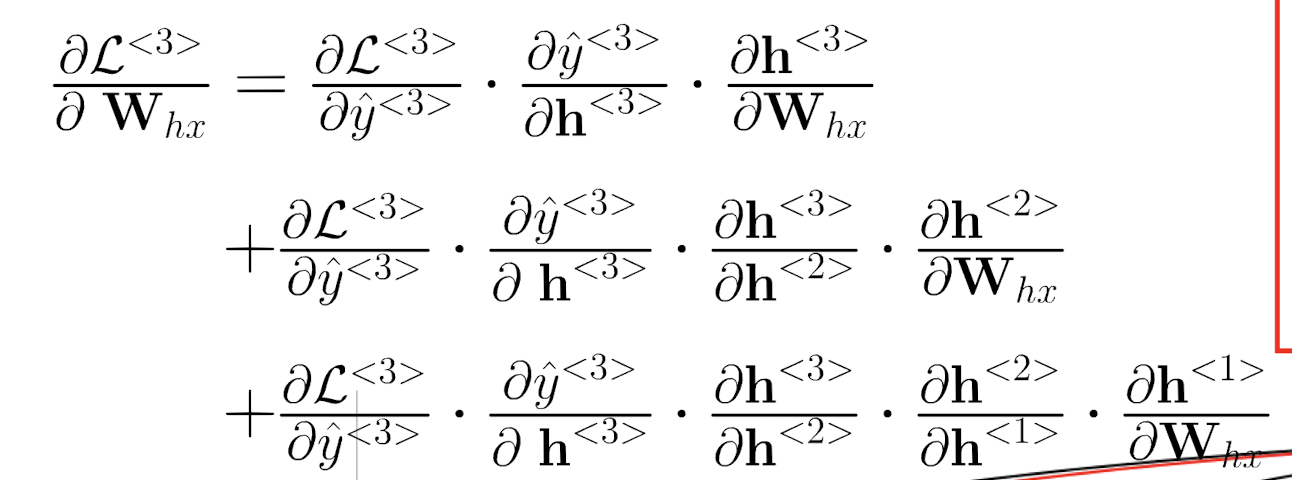
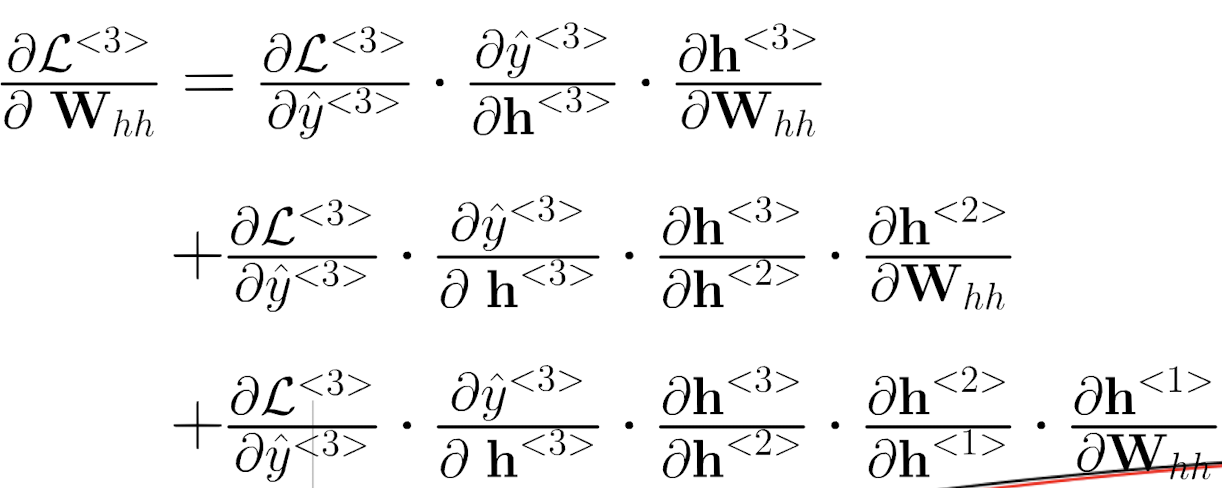
以上两个求导公式是一致的。

h之间的比值就是一个激活函数的导数。

长程依赖问题

1. 梯度爆炸——可以采用梯度削减来缓解
2. 梯度消失——可以选取更好的激活函数或者改变传播结构
3. 记忆容量问题：信息单元输入东西，是一个累加的过程，随着长度增加，值越来越大，造成$tanh$达到饱和。这样的感觉就是容器存储满了，之后的信息产生的影响不大，相当于被舍弃。
   2、3亮点互为表里，是等价的。

当$tanh\times {\omega }_{hh/hx}\ge 1$时，出现梯度爆炸，反之梯度消失。

最后

以上就是雪白豆芽为你收集整理的循环神经网络_基础的全部内容，希望文章能够帮你解决循环神经网络_基础所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。