MATLAB：对于状态空间方程的系统辨识

本文介绍了如何利用MATLAB辨识状态空间方程中的未知参数。

假设我们的被控系统的表达如下：

$$\dot{X}=\left[\begin{array}{cc}0& 1\\ K_1& K_2\end{array}\right]X+BU$$
$$Y=X$$

我们想要通过实验数据辨识出参数$K_1$和$K_2$，方法如下：

第一步，采集实验数据。

需要的数据包括系统一段时间内的系统输出$Y(t_s)$，以及控制量$U(t_s)$，这些数据应该是以某个固定的采样频率进行采集得到的。另外，最好是要采集系统的初始状态（虽然这个初始状态也是可以辨识的，但能采集到尽量就采集到）。

第二步，运用MATLAB进行辨识

代码如下，重要的步骤都体现在注释中了：

clc;
clear all;
close all;
format long

%%  读取数据，这一部分大家按照自己的应用来更改
data = xlsread('nopec-static-4.xlsx');
t = data(:,1) - data(1,1);
x1 = data(:,2)/360*2*pi - 0.1;
x2 = data(:,3)/16.4/57.3;
x = [x1,x2]; 
u1 = zeros(size(x1));
u2 = zeros(size(x2));
u = [u1, u2];

%% 搭建状态空间模型
% dot(X) = AX + BU + Ke
% Y = CX + DU +e
% 上式是idss默认的状态空间模型的形式
A = [0, 1; -0.1, -0.1];
B = zeros(2,2);
C = eye(2,2);
D = zeros(2,2);
K = zeros(2,2);
x0 = [x1(1);0];
m = idss(A,B,C,D,'Ts',0); % 构建模型 % 关键函数

% 变量的优化设置
m.Structure.A.Free(1,1) = false; % 这里设置为false，代表A(1,1)这个变量是不可优化的
m.Structure.A.Free(1,2) = false; 
m.Structure.A.Value(2,1) = -10; % 这里设置的是A(2,1)的初始值
m.Structure.A.Value(2,2) = -10; % 这里参数初始值的设置非常重要，初始值设置得不对，最后辨识的结果往往都不会太好
m.Structure.B.Free = false;
m.Structure.C.Free = false;
m.Structure.D.Free = false;
m.Structure.K.Free = false;

%% 打包用于辨识的数据，x是输出，u是控制输入，0.1是采样时间间隔
z = iddata(x,u,0.1); % 关键函数

%% 模型辨识
% 关于辨识过程中的设置，比如优化的cost容忍范围，以及迭代次数，以及状态X的初始条件等等
% 更多关于辨识和优化过程的设置，可以参考：help ssestOptions
opt = ssestOptions;
% opt.InitialState = idpar(x0); % 这里可以设置初始状态也是可优化的
opt.InitialState = x0; % 设置初始状态
opt.SearchOption.Tolerance = 0.01; %设置误差范围
opt.SearchOption.MaxIter = 500; % 设置最大迭代次数
opt.Display = 'full'; %设置是否显示辨识过程
% 模型辨识
m = ssest(z,m,opt); % 关键函数

%% 模型验证 
uu = idinput([150,2]);
simdat = iddata([],uu,'Ts',0.1);
simopt = simOptions('InitialCondition', x0);
y = sim(m,simdat,simopt); % 关键函数
y1 = y.OutputData(:,1);
y2 = y.OutputData(:,2);

%% 绘图
figure(1)
subplot(2,1,1)
plot(x1,'r','LineWidth',3)
hold on
plot(y1,'g','LineWidth',3)
hold on
grid on
xlabel('X1')
legend('实际系统','辨识系统')
subplot(2,1,2)
plot(x2,'r','LineWidth',3)
hold on
plot(y2,'g','LineWidth',3)
hold on
grid on
xlabel('X2')
legend('实际系统','辨识系统')

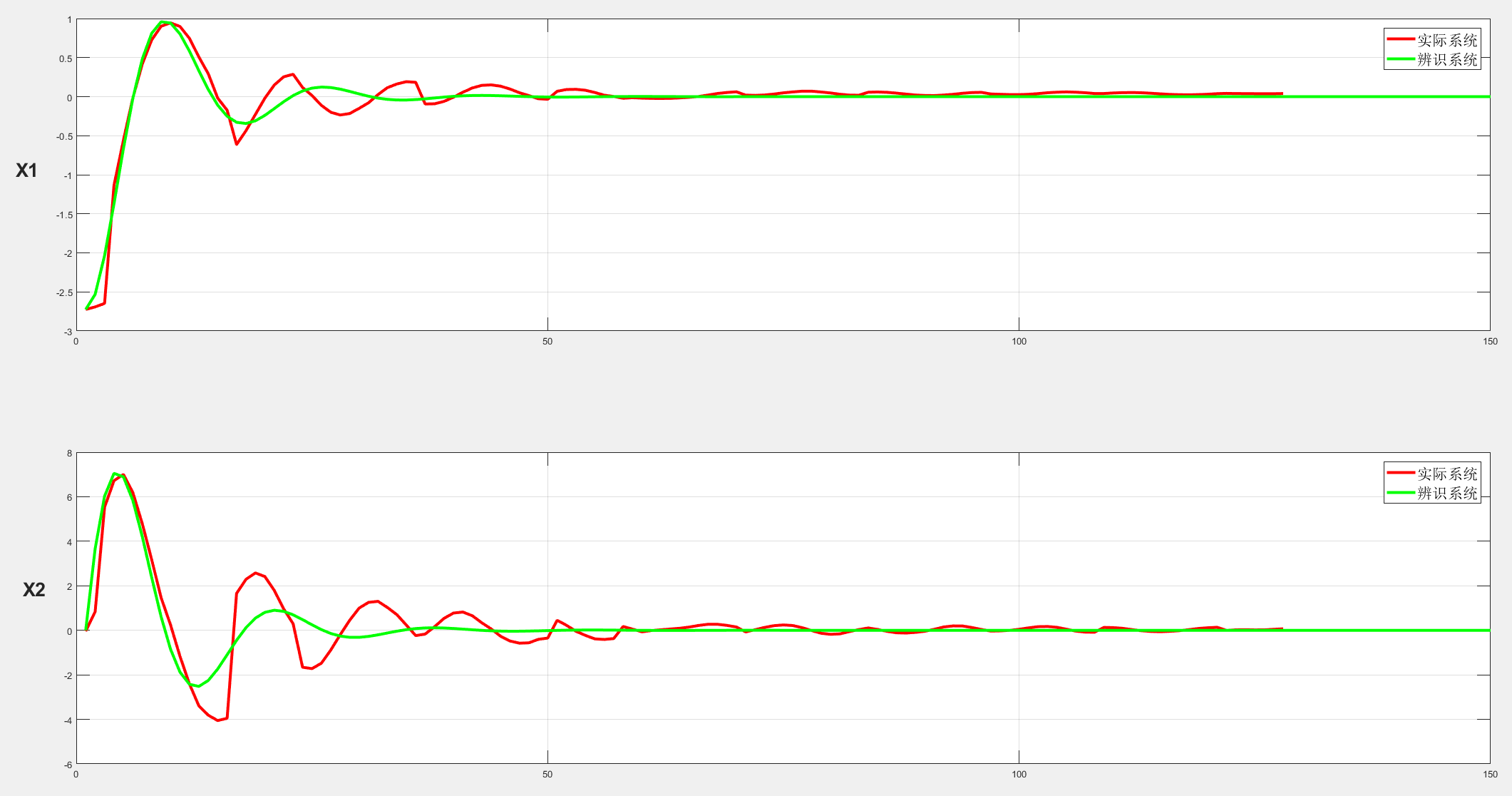
第三步，检查辨识结果

这是我的实验数据，辨识得到的结果，我还是比较满意的，大家可以在自己的应用中，多试几组数据，对比每次辨识出的参数结果，看看是否稳定。

推荐资料

Estimate State-Space Models with Structured Parameterization

最后

以上就是活泼含羞草为你收集整理的MATLAB：对于状态空间方程的系统辨识MATLAB：对于状态空间方程的系统辨识的全部内容，希望文章能够帮你解决MATLAB：对于状态空间方程的系统辨识MATLAB：对于状态空间方程的系统辨识所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。