一、功能部件——加法器
1. 全加器
全加器——将两位本地二进制数和1位低位进位的数进行相加,求的1位本地结果以及1位向高位进位的结果。简单来说就是3个input,2个output,这里的逻辑比较简单,我就不具体介绍了。
下图所示的数全加器的逻辑图,这里我们需要分析一下门的延迟,得到进位Cout需要2级门的延迟,得到结果S需要3级门的延迟。这个延迟需要特别留意,对后面分析问题比较重要‼️
图1:
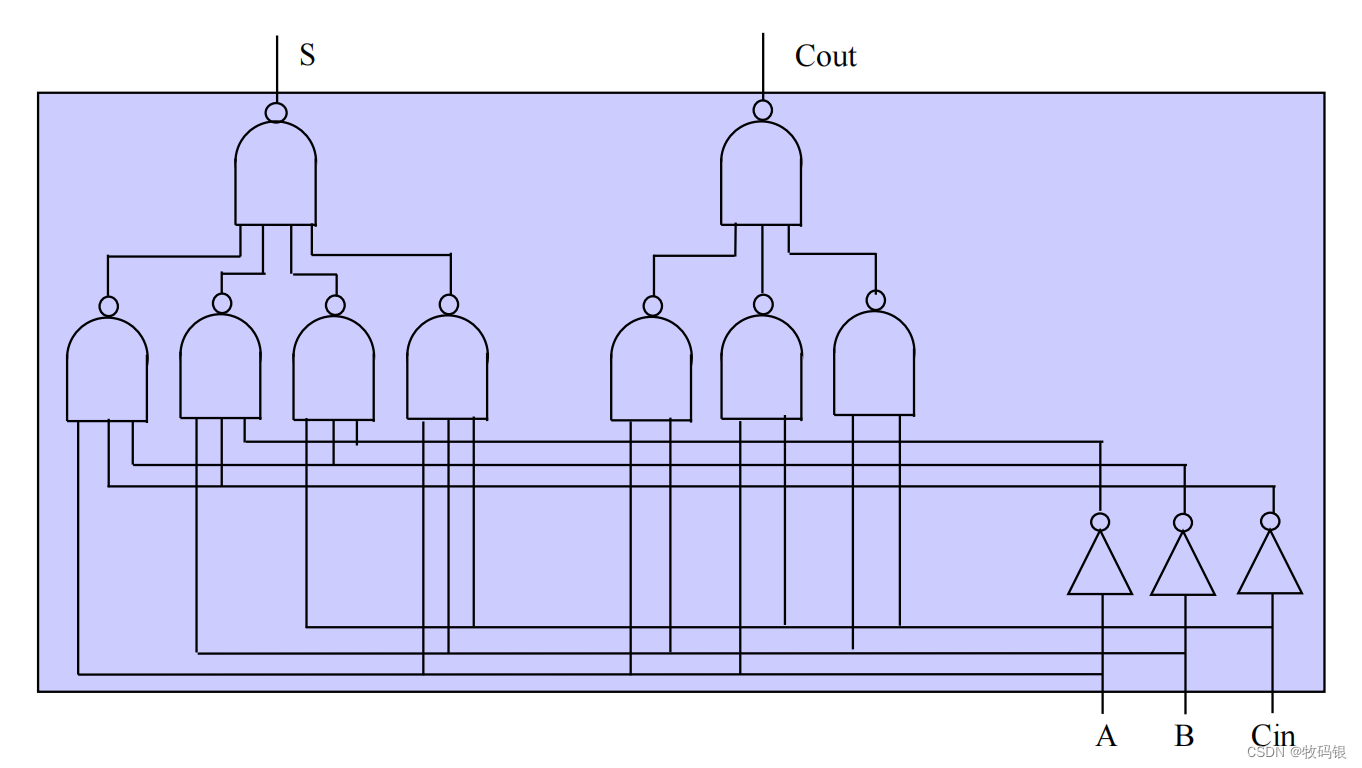
图2:
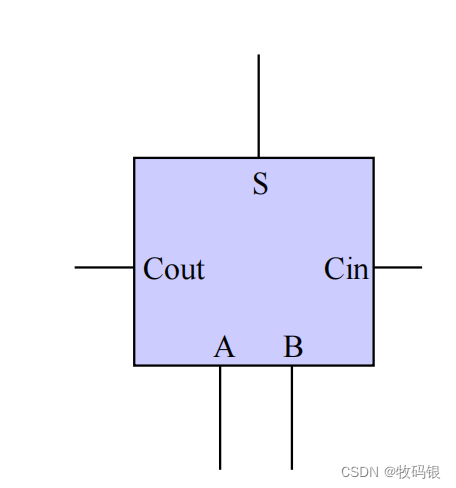
2 串行进位加法器
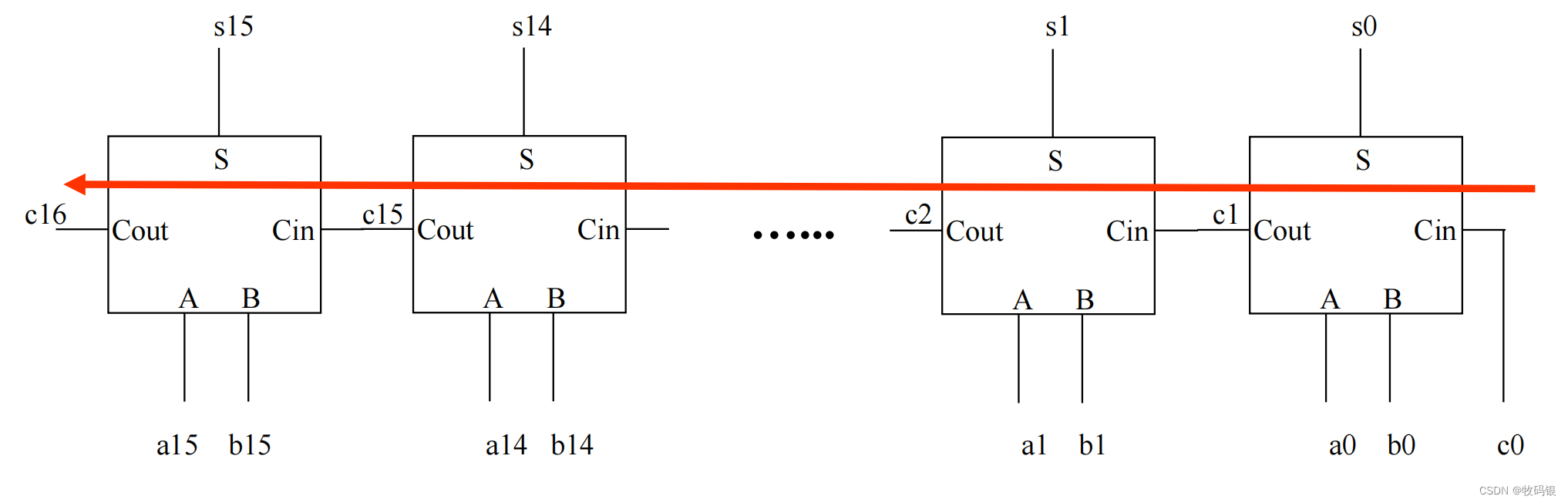
所谓串行进位加法器就是把多个全加器进行串接起来,低位的Cout接到高位的Cin,依次串联。
下图所示即为串行进位加法器,从我们刚才分析全加器的门延迟来看,这里得到c16需要(16 * 2)=32级门延迟,得到s15则需要(15 * 2+3)=33级门延迟。
解释:这里我稍微解释一下怎么计算的,得到c16我想大家能想明白,就是每一级的Cin到Cout都需要2级门的延迟,所以一共16个全加器就是32级门的延迟。s15的计算就是到c15的时候是30级门的延迟,再加上最后这个全加器,Cin到S的这个3级门的延迟,所以总共是33级门延迟。
图3:
3 先行进位加法器
工程师说这个串行进位的32级门延迟太慢了,所以又进行了改进。
这里的先行进位加法器,就是通过加快进位传递来加快速度的加法器。主要思想就是并行计算每一位的进位。
下面就开始比较绕了,要慢慢理解。
首先假设有两个N位数相加,被加数为A = a
N
−
1
_{N-1}
N−1a
N
−
2
_{N-2}
N−2……a
i
_{i}
ia
i
−
1
_{i-1}
i−1……a
1
_{1}
1a
0
_{0}
0 ,加数为B = b
N
−
1
_{N-1}
N−1b
N
−
2
_{N-2}
N−2……b
i
_{i}
ib
i
−
1
_{i-1}
i−1……b
1
_{1}
1b
0
_{0}
0 ,相加的和为S = s
N
−
1
_{N-1}
N−1s
N
−
2
_{N-2}
N−2……s
i
_{i}
is
i
−
1
_{i-1}
i−1……s
1
_{1}
1s
0
_{0}
0 ,第i位的进位输入为c
i
_{i}
i,进位输出为c
i
+
1
_{i+1}
i+1。
首先介绍几个概念:
进位生成因子:g
i
_i
i = a
i
_i
i & b
i
_i
i
进位传递因子:p
i
_i
i = a
i
_i
i|b
i
_i
i
我们在没有进位生成因子和进位传递因子之前,我们是如何来表示c
i
+
1
_{i+1}
i+1的呢?
c
i
+
1
_{i+1}
i+1 =( a
i
_i
i & b
i
_i
i) | (a
i
_i
i & c
i
_i
i) | (b
i
_i
i & c
i
_i
i) = (a
i
_i
i & b
i
_i
i) | (a
i
_i
i | b
i
_i
i) & c
i
_i
i
但是当引入g
i
_i
i和p
i
_i
i之后,我们就可以简化这个表达式:
c
i
+
1
_{i+1}
i+1 = g
i
_i
i|p
i
_i
i & c
i
_i
i
如果还不是很懂,那么我举个例子来帮助理解
就用一个四位加法器来解释:
首先我们罗列出c
i
_i
i的展开式:
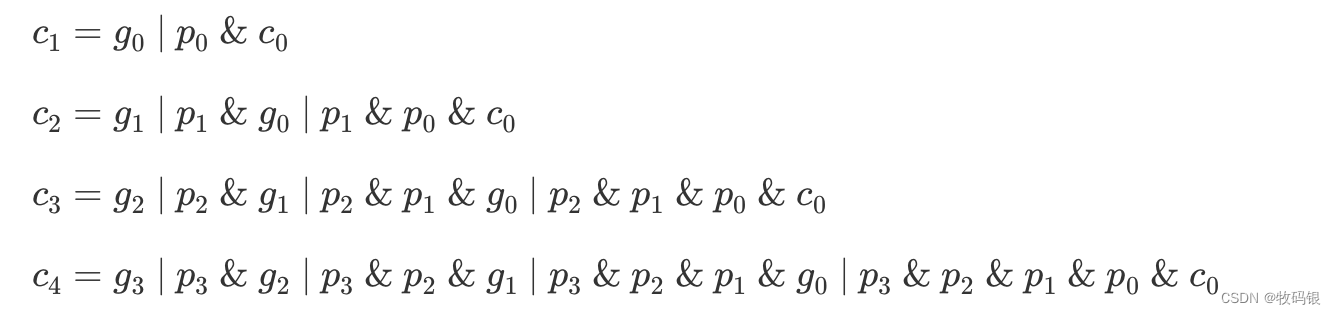
解释:
拿c1来看,有两种情况c1能为1 ,第一种情况,就是a
0
_0
0和b
0
_0
0都为1,也就是生成因子g
0
_0
0为1,那肯定能生成进位;第二种情况就是a
0
_0
0和b
0
_0
0中只有一个为1,也就是p
0
_0
0为1,再另加上c
0
_0
0为1 ,这样也能生成进位。其他c
i
_i
i类似。
下图4是一个4位的并行进位的逻辑图
首先我要说的是,产生p
i
_i
i 和 g
i
_i
i 是两级门延迟,为什么呢?因为在cmos实现的时候 与门 = 与非门+非门 、 或门 = 或非门 + 非门,所以是两级门的延迟。
再来对比一下,这里产生c 4 _4 4是2级门的延迟,而串行进位则是8级门的延迟,确实是减少了很多的延迟。那就会有同学问,能不能做成64位的?emmm,答案是理论上可以但现实不可以,为什么,看这个例子中,有一个5输入的与非门,这个多输入与非门的延迟是非常大的,一般我们最多用4级,所以我们不能无限扩展位数。那怎么才能实现64位的呢?往下看。
图4:
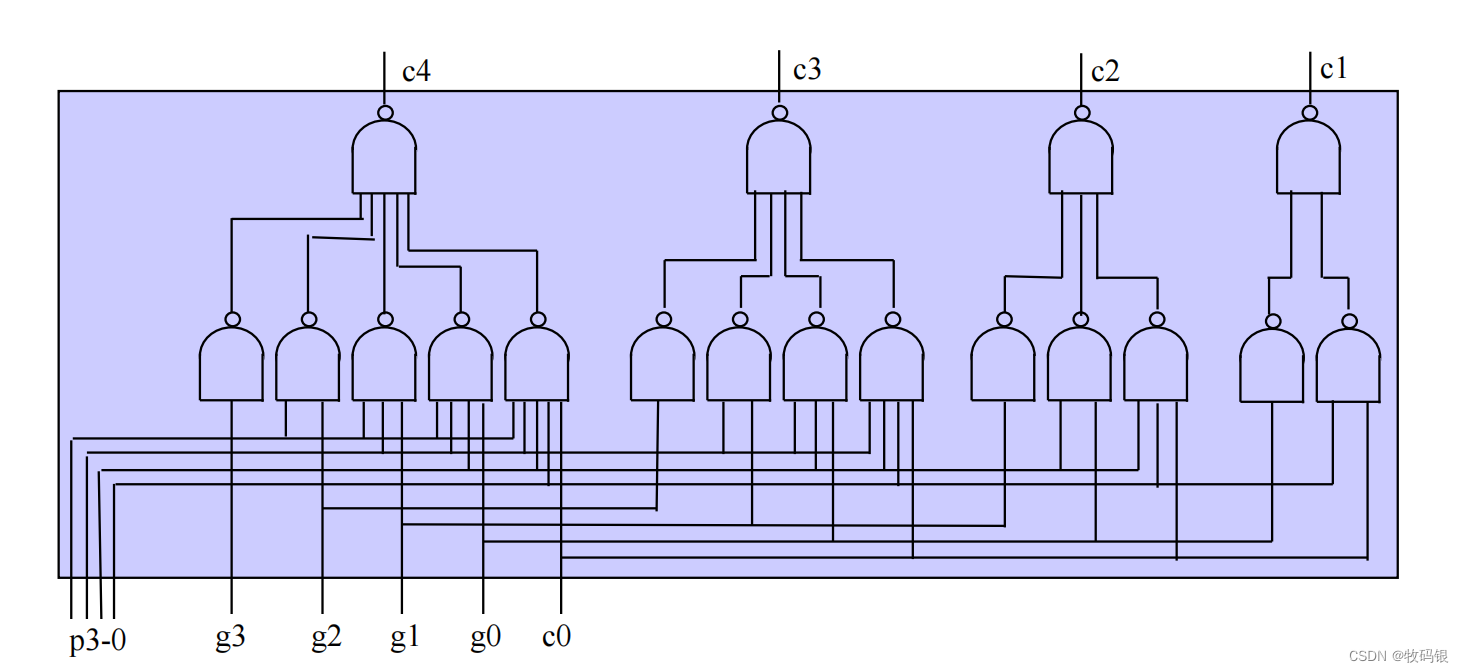
图5:
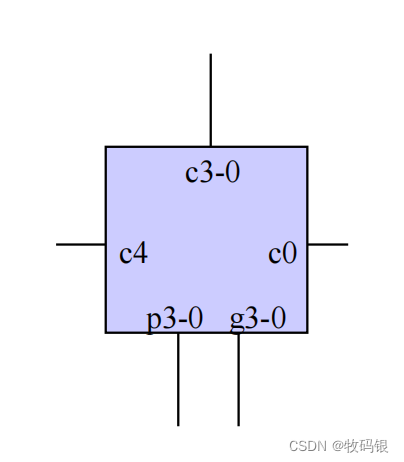
刚才我们说不能无限扩展位数,那还有什么其他办法能做到呢?
那工程师又提出一个解决办法:分块,实现块内并行,块间串行的加法器。
如图6是一个16位加法器逻辑图:
图6:
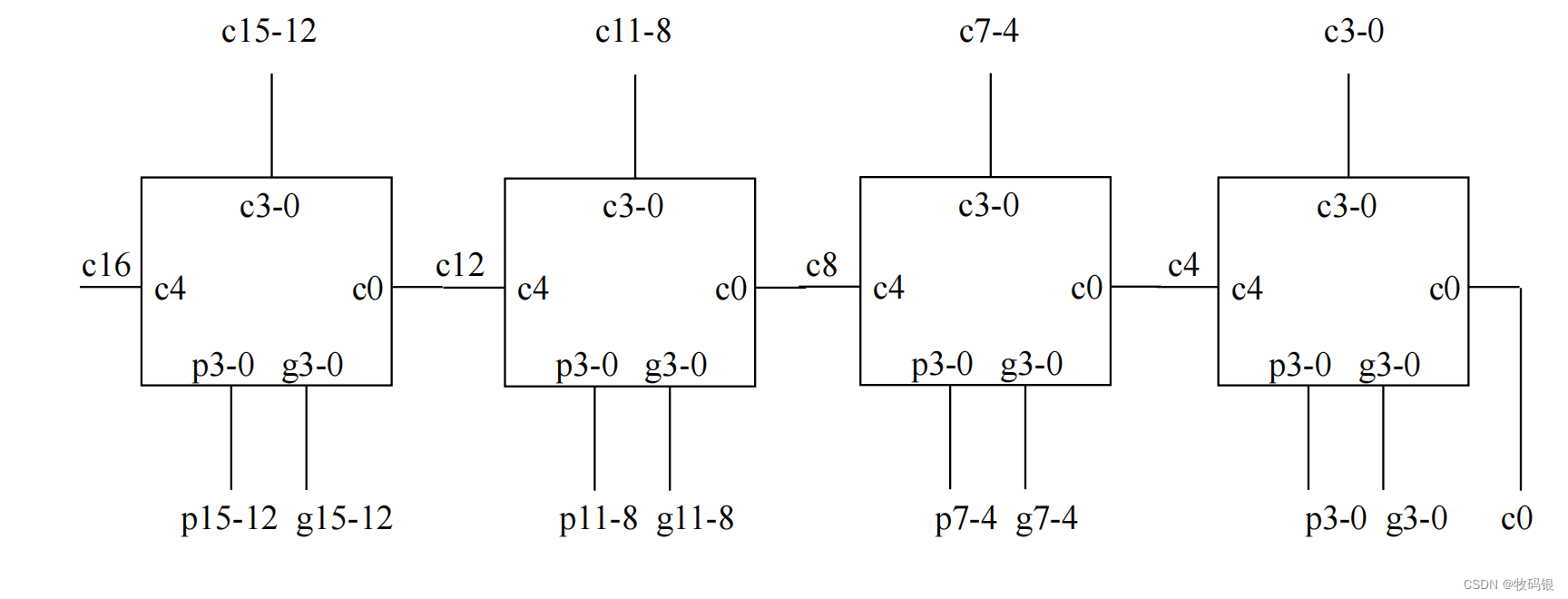
这里采用的是块内并行,块间串行,那得到c15的门延迟为(4 * 2) = 8级门延迟,因为块内产生4位进位只需要2级门的延迟。还不懂的往上看一下图4,从p
i
_i
i 、 g
i
_i
i到c
1
−
4
_{1-4}
1−4是不是只需要2级门的延迟。对比一下,从串行进位的32级门,到现在的8级门延迟,好像已经降低了很多很多了,但是还不够,继续优化。
为了进一步提升加法器的速度,我们在块间也采用了先行进位的方法。
块间也采用先行进位,那么跟上面产生p
i
_i
i 、 g
i
_i
i一样,这里块间进位也需要进位生成因子G 和进位传递因子 P。
块间进位生成因子:G = g
3
_3
3|( p
3
_3
3 & g
2
_2
2 )|( p
3
_3
3 & p
2
_2
2 & g
1
_1
1 ) | ( p
3
_3
3 & p
2
_2
2 & p
1
_1
1 & g
0
_0
0 );
块间进位传递因子:P = p
3
_3
3 & p
2
_2
2 & p
1
_1
1 & p
0
_0
0 ;
图7:
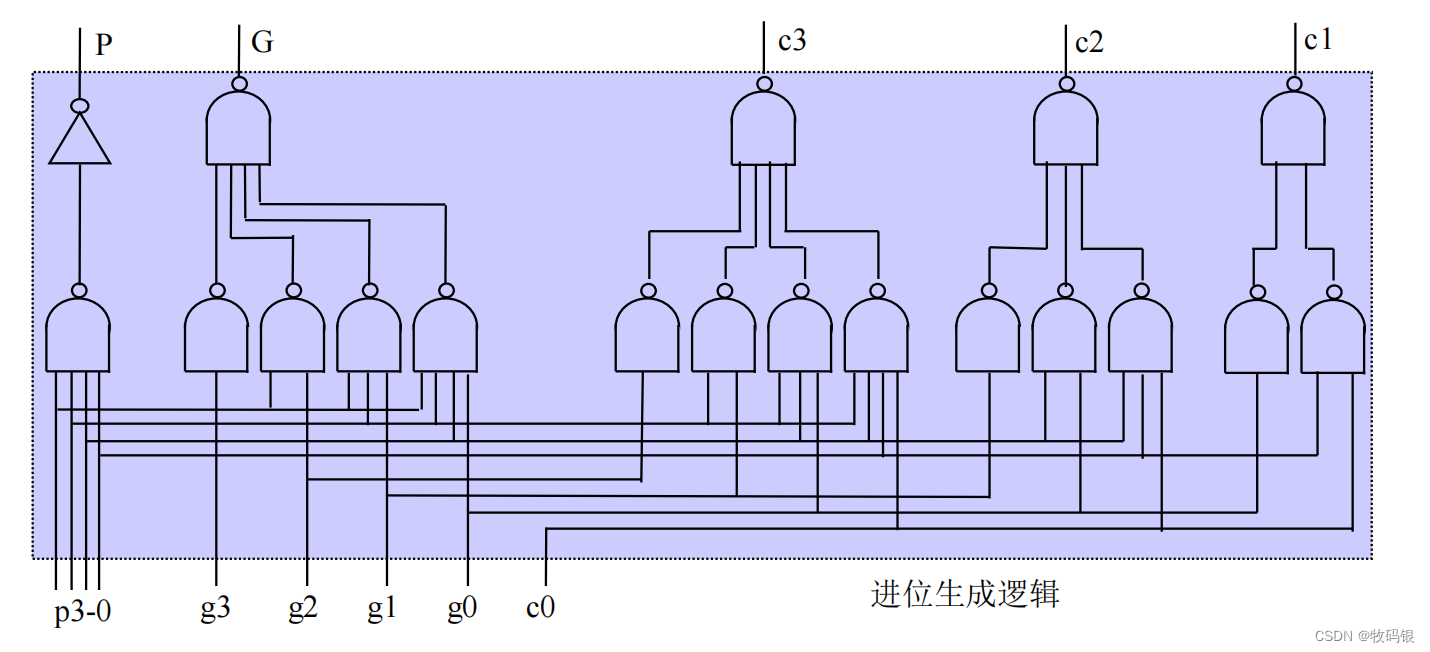
图8:
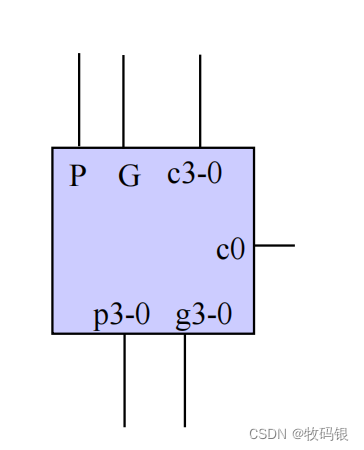
图7是一个四位的进位生成逻辑,而且是包含了P和G。
那一起看一下16位的块内并行、块间并行的逻辑图。
图8:
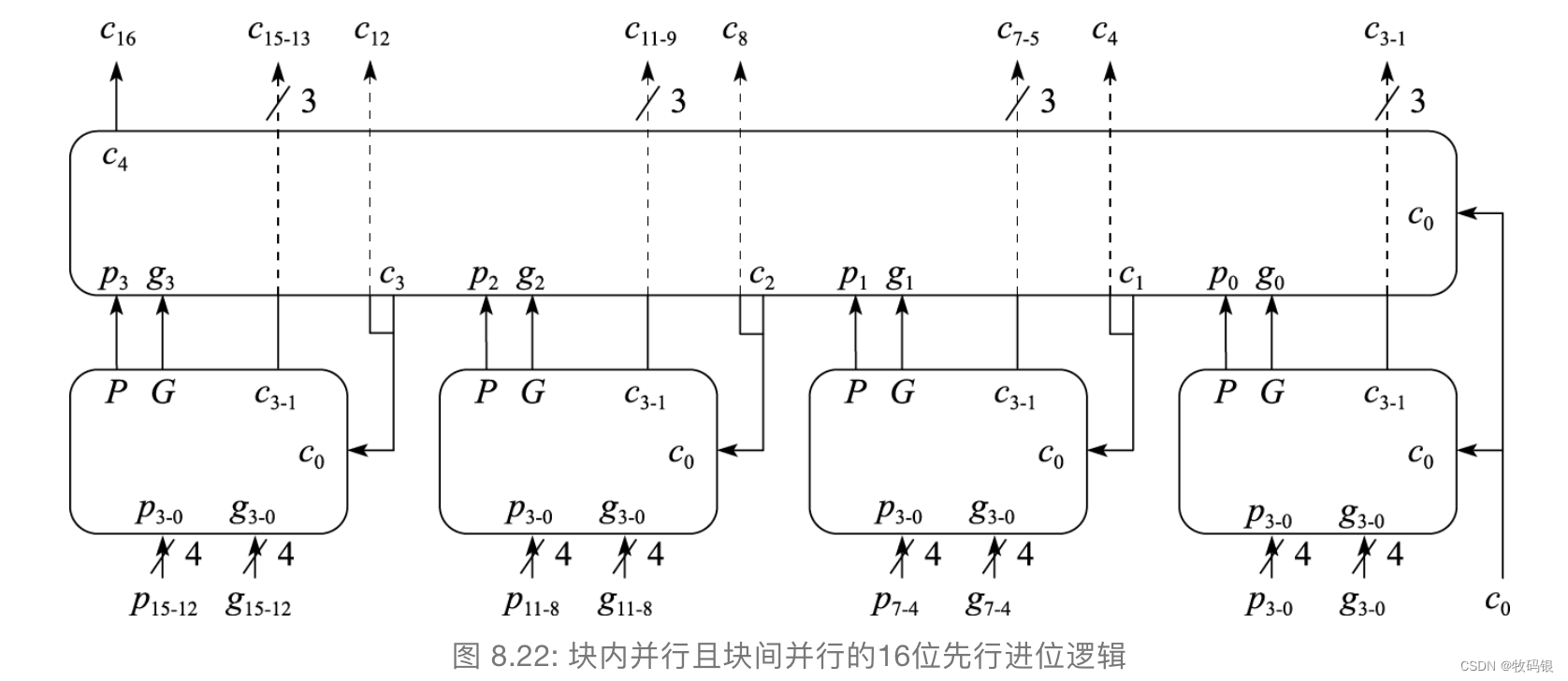
看这张图需要看两层,底下这一层是4个4位的进位逻辑,产生了第二层的p
i
_i
i 和 g
i
_i
i。
这里比较难理解,我重点解释一下。
图8:
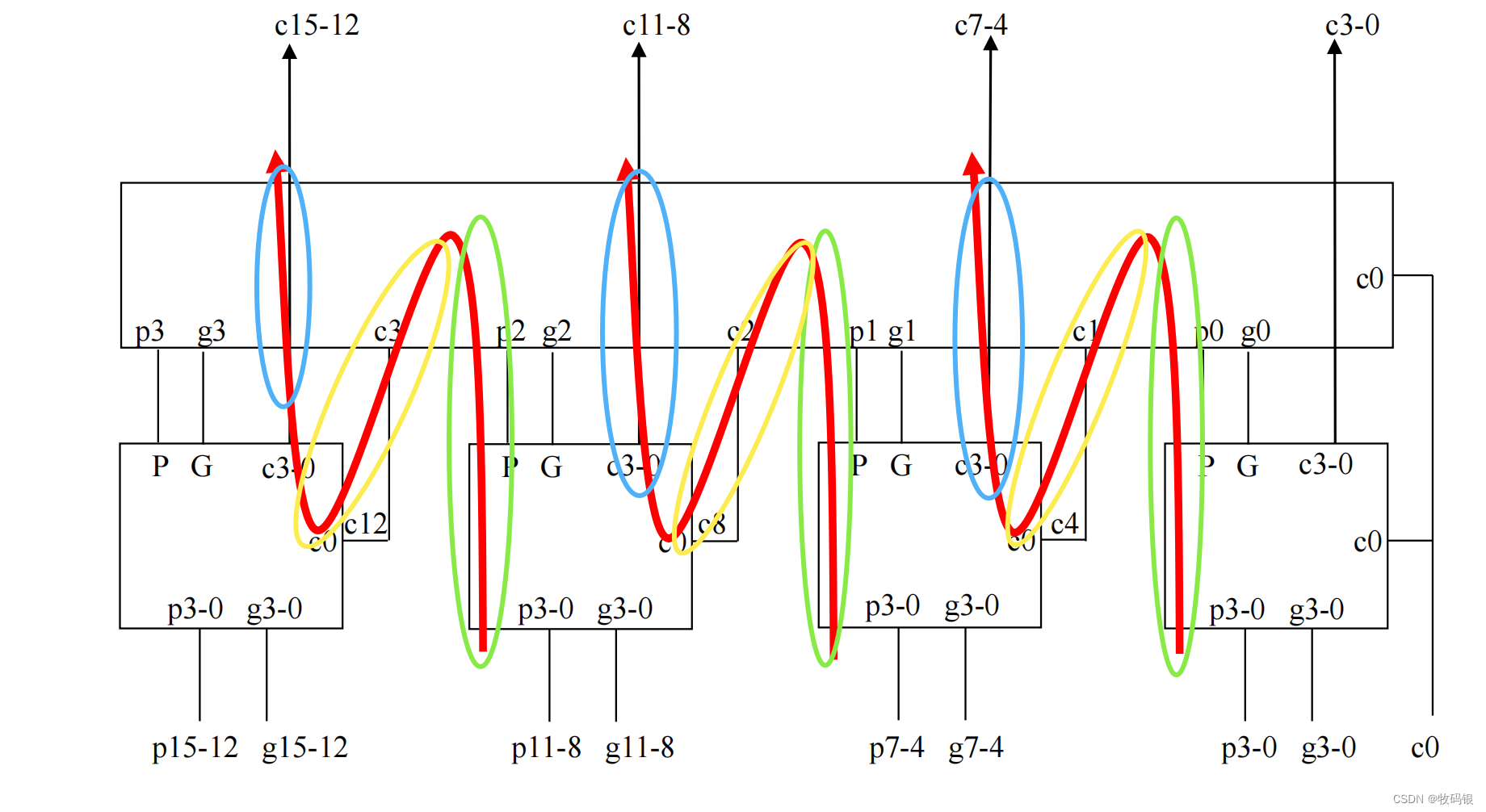
结合这张图,我们来看这个执行过程,首先是每一个块内由p
i
_i
i 和 g
i
_i
i生成P 、G,这里可以看图7,一共是2级门的延迟,对应的是图8绿圈部分。第二步是通过第二层(上层)的这个4位进位逻辑产生了c
4
_4
4、c
8
_8
8、c
12
_{12}
12,这里不知道大家能不能理解,因为第一层(底层)的P和G是作为第二层(上层)的p
i
_i
i 和 g
i
_i
i输入的,所以可以由此产生进位c,这步操作也是2级门的延迟,对应的是黄圈部分。第三步是由底层的这4个进位逻辑,产生c
5
−
7
_{5-7}
5−7、c
9
−
11
_{9-11}
9−11、c
13
−
15
_{13-15}
13−15,这个也是2级门的延迟,对应的图中是蓝圈部分。
所以综上,得出块内并行、块间并行进位逻辑总共的延迟为6级门的延迟,也就是说一个16位先行进位加法器一共需要(2 + 6 + 3) = 11级门延迟,这里的2是产生p
i
_i
i 和 g
i
_i
i的,6是先行进位逻辑产生的,3是从c到结果s产生的。
好啦,我们从串行进位的32级门延迟——>块内并行,块间串行8级门延迟——>块内并行、块间并行6级门延迟,那么优化也到这里就告一段落了。
检测一下大家有没有真的学懂,采用块内并行、块间并行实现64位加法器一共是多少级门延迟呢?
解答一下吧:
答案是(2+10+3) = 15级门延迟。
不会算的话我再简单教一下:
图9:
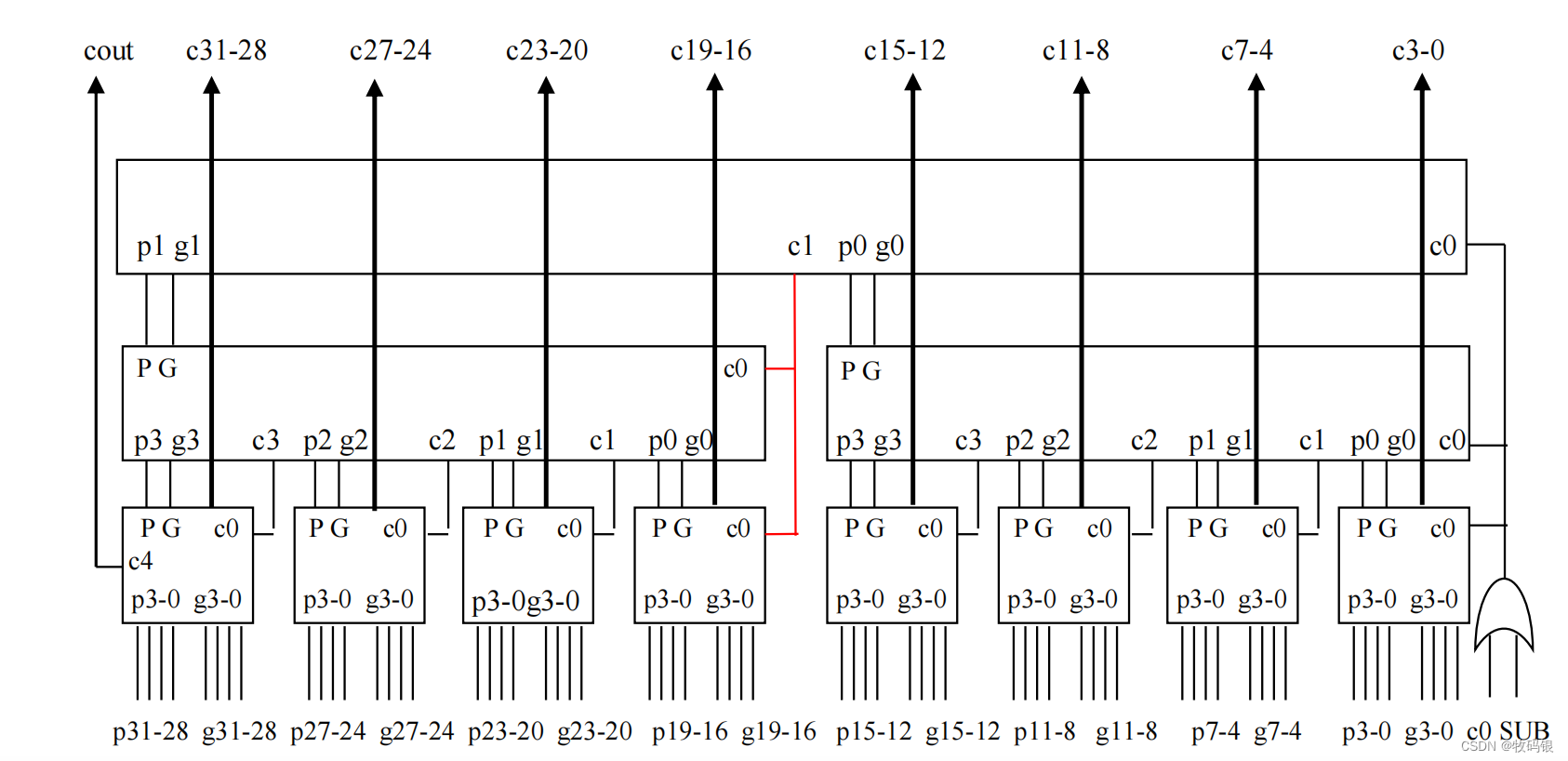
这是一个块内并行、块间并行32位的加法器,和64的原理一样,我就拿这个图来解释。(从下往上依次为第一、第二、第三层)
第一层的p
i
_i
i 和 g
i
_i
i产生P和G传递给第二层的p
i
_i
i 和 g
i
_i
i,这里需要2级门的延迟;
第二层的p
i
_i
i 和 g
i
_i
i生成P和G传递给第三层的p
i
_i
i 和 g
i
_i
i,这里需要2级门的延迟;
第三层的p
i
_i
i 、g
i
_i
i 以及 c
0
_0
0 产生c
16
_{16}
16 传递给第二层,也就是图中的红线部分,这里需要2级门的延迟;
第二层的p
i
_i
i 、g
i
_i
i 以及 c
16
_{16}
16 产生c
16
_{16}
16、c
20
_{20}
20、c
24
_{24}
24、c
28
_{28}
28传递给第一层,这里需要2级门的延迟;
第一层通过p
i
_i
i 、g
i
_i
i 以及 c
0
_0
0产生了c
16
−
19
_{16-19}
16−19、c
20
−
23
_{20-23}
20−23等等进位信号,这里需要2级门的延迟;
这样这个32/64位的先行进位加法器的进位逻辑部分就是10级门的延迟,加上之前说的,产生第一层p
i
_i
i 、g
i
_i
i 时需要的2级门延迟,加上第三层进位信号c
i
_i
i到结果S需要的3级门延迟,就是一共15级门的延迟。
图10:
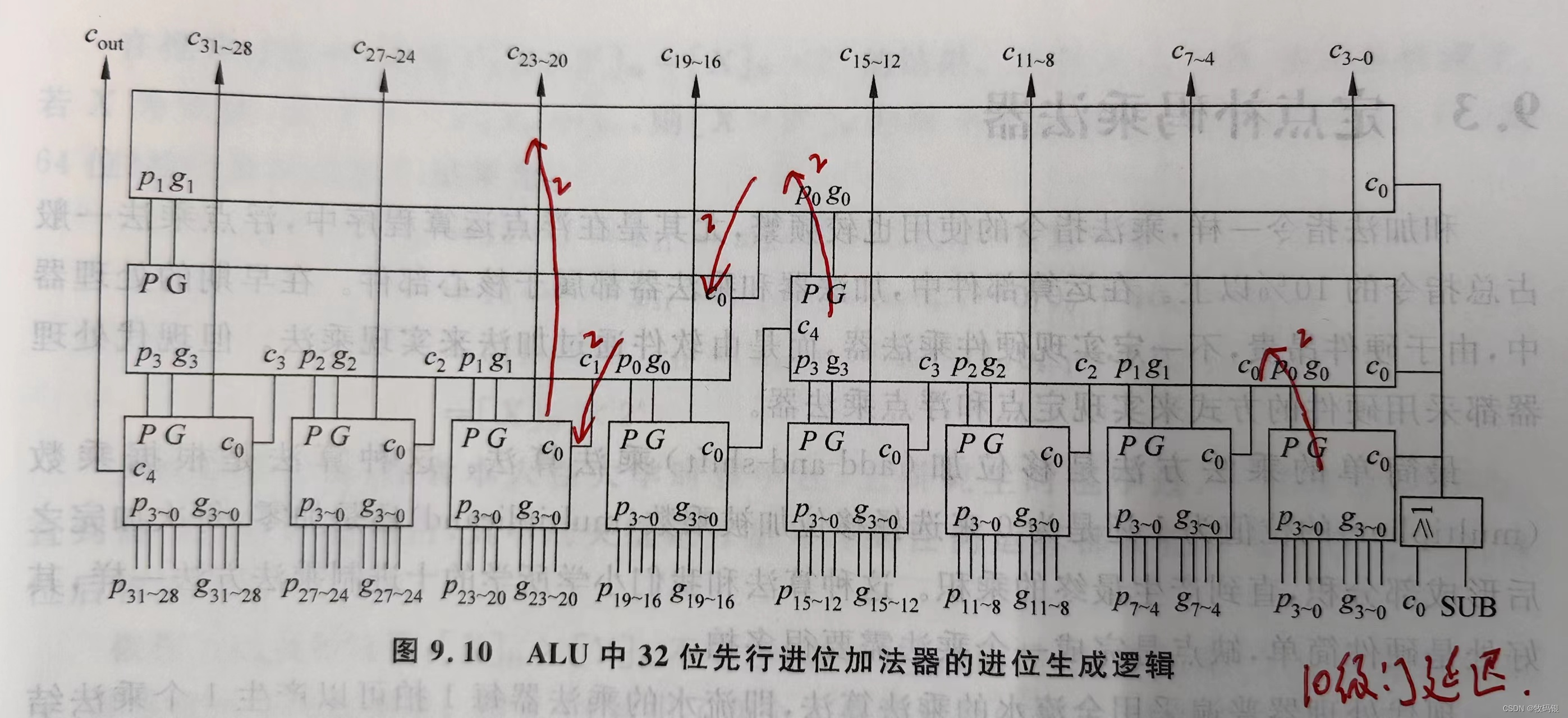
图11:

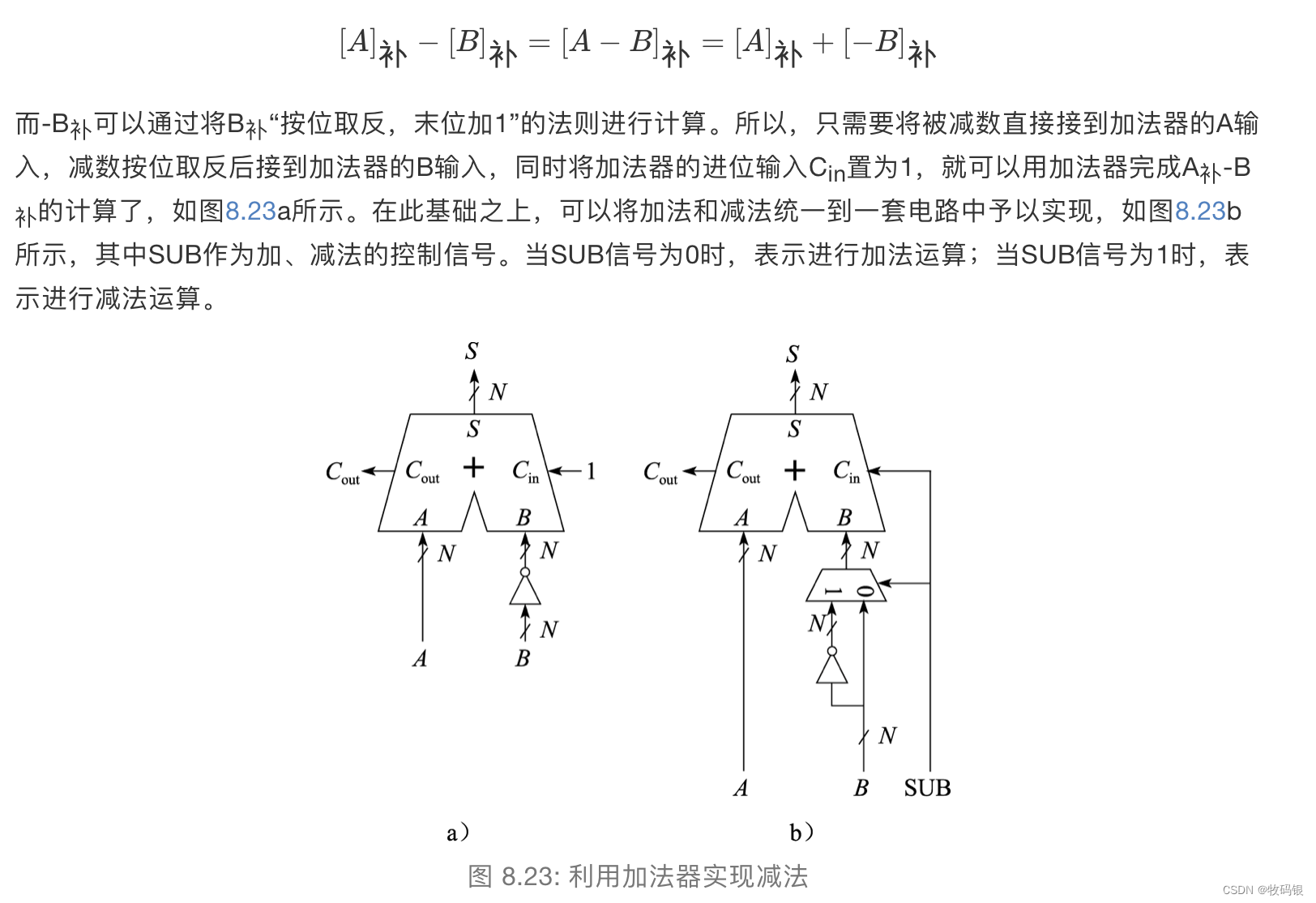
4 减法操作
这应该不用详细介绍了,就是利用加法器来实现减法操作,贴张图简单看一看就行,就是在加法器之前加一个二选一的逻辑,是减法的话就把被加数[B]
补
_补
补取反加1即可。
二、功能部件——乘法器
这是一个难点,在学这个之前,我们先来了解一下补码的定义。
补码的定义是什么?
假设 [Y]
补
_补
补 = y
31
_{31}
31y
30
_{30}
30……y
1
_{1}
1y
0
_{0}
0 ,那么我们怎么计算这个Y的值呢?
Y = - y
31
_{31}
31 * 2
31
^{31}
31 + y
30
_{30}
30 * 2
30
^{30}
30 + …… + y
1
_{1}
1 * 2
1
^{1}
1 + y
0
_{0}
0 * 2
0
^{0}
0
知道了Y的值是怎么计算的,那么我们是不是就能求[X*Y]
补
_补
补了呢?
[X * Y]
补
_补
补 = [X]
补
_补
补 * Y
其实很简单,我们知道 [X + Y]
补
_补
补 = [X]
补
_补
补 + [Y]
补
_补
补,那么[X * Y]
补
_补
补就是Y个 [X]
补
_补
补相加的结果。
图12:

举个例子,我们根据补码的定义,我们可以非常方便的计算两个数的相乘,只不过这里需要注意的是一定要进行符号扩展后才可以进行相加,而且只需要对y的最高位进行减操作,其他位都是加操作,最后这个减操作也很简单,只需要“按位取反,末尾加1”即可。
1 一位Booth算法
Booth夫妇把补码乘法的每一位的部分积都统一成相同的形式,通过每次扫描乘数的2位来确定乘积项。
图13:
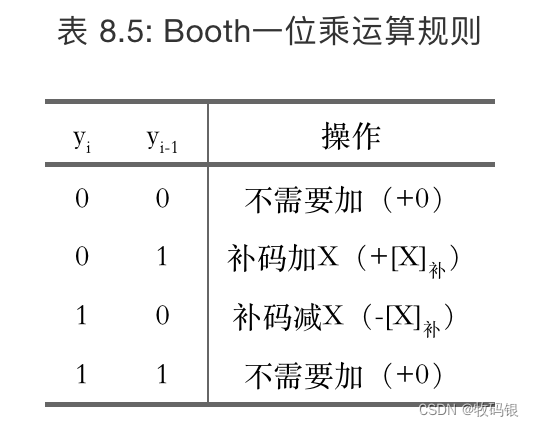
为什么数这样的运算规则呢?
来看看Booth夫妇对补码定义公式进行的改动。
Y = - y 31 _{31} 31 * 2 31 ^{31} 31 + y 30 _{30} 30 * 2 30 ^{30} 30 + …… + y 1 _{1} 1 * 2 1 ^{1} 1 + y 0 _{0} 0 * 2 0 ^{0} 0
===> Y = ( y 30 _{30} 30 - y 31 _{31} 31) * 2 31 ^{31} 31 + ( y 29 _{29} 29 - y 30 _{30} 30 ) * 2 30 ^{30} 30 + …… + ( y 0 _{0} 0 - y 1 _{1} 1 ) * 2 1 ^{1} 1 + ( y − 1 _{-1} −1 - y 0 _{0} 0) * 2 0 ^{0} 0
其中y − 1 _{-1} −1 为0
来看刚才两个四位数相乘的例子:
图14:

其实改动并不大,这个一位Booth乘法只是把部分积形式统一了一下而已,并没有加快多少运算速度。
2 两位Booth算法
这算是非常大的优化了,首先让我们看一下如何优化表达式的:
Y = - y
31
_{31}
31 * 2
31
^{31}
31 + y
30
_{30}
30 * 2
30
^{30}
30 + …… + y
1
_{1}
1 * 2
1
^{1}
1 + y
0
_{0}
0 * 2
0
^{0}
0
===> Y = ( y 30 _{30} 30 - y 31 _{31} 31) * 2 31 ^{31} 31 + ( y 29 _{29} 29 - y 30 _{30} 30 ) * 2 30 ^{30} 30 + …… + ( y 0 _{0} 0 - y 1 _{1} 1 ) * 2 1 ^{1} 1 + ( y − 1 _{-1} −1 - y 0 _{0} 0) * 2 0 ^{0} 0
===> Y = ( y 29 _{29} 29 + y 30 _{30} 30 - 2 * y 31 _{31} 31) * 2 30 ^{30} 30 + ( y 27 _{27} 27 + y 28 _{28} 28 - 2 * y 29 _{29} 29 ) * 2 28 ^{28} 28 + …… + ( y 1 _{1} 1 + y 2 _{2} 2 -2 * y 3 _{3} 3 ) * 2 2 ^{2} 2 + (y − 1 _{-1} −1 + y 0 _{0} 0 - 2 * y 1 _{1} 1) * 2 0 ^{0} 0
每次可以扫描乘数的3位来确定乘积项,这样乘积项就少了一半。
图15:
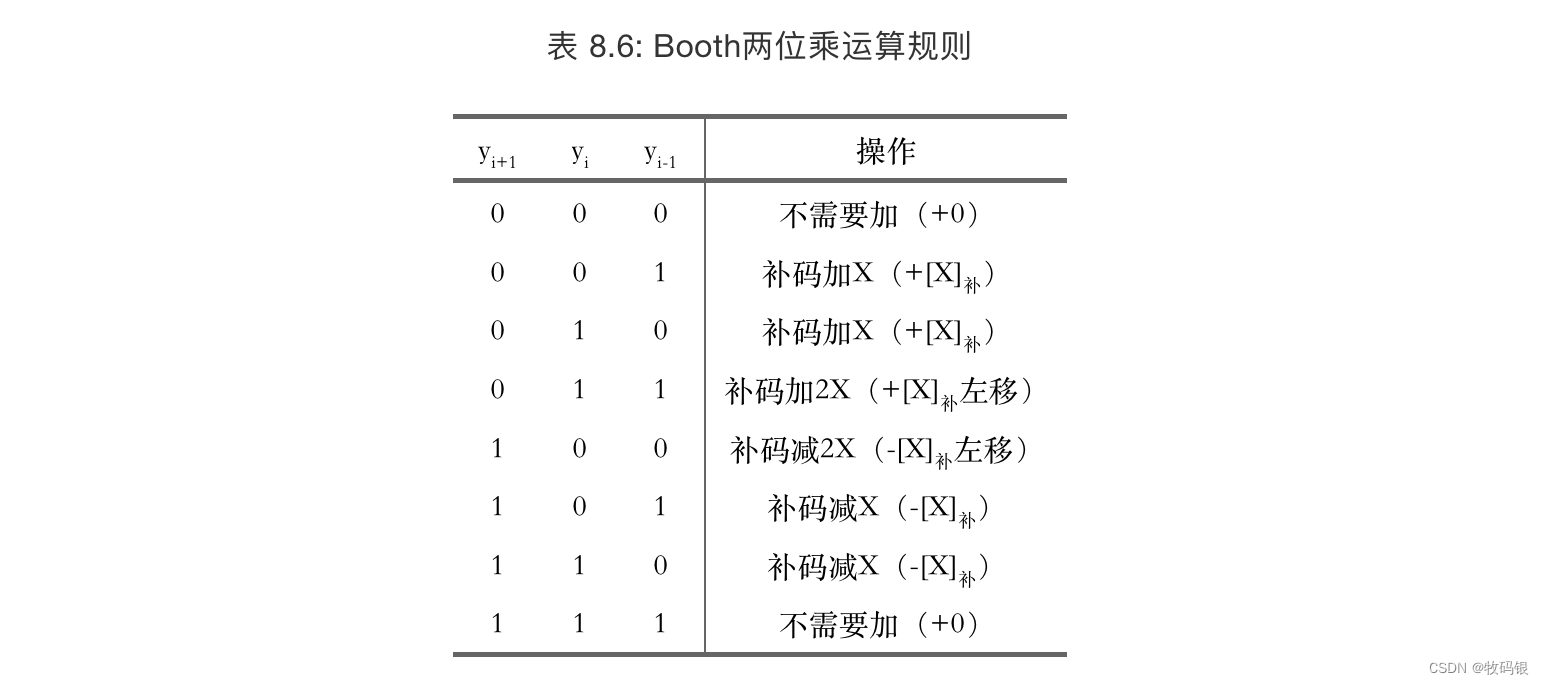
来看看具体例子:
是不是相较于上面的一位Booth运算量减少了很多
图16:
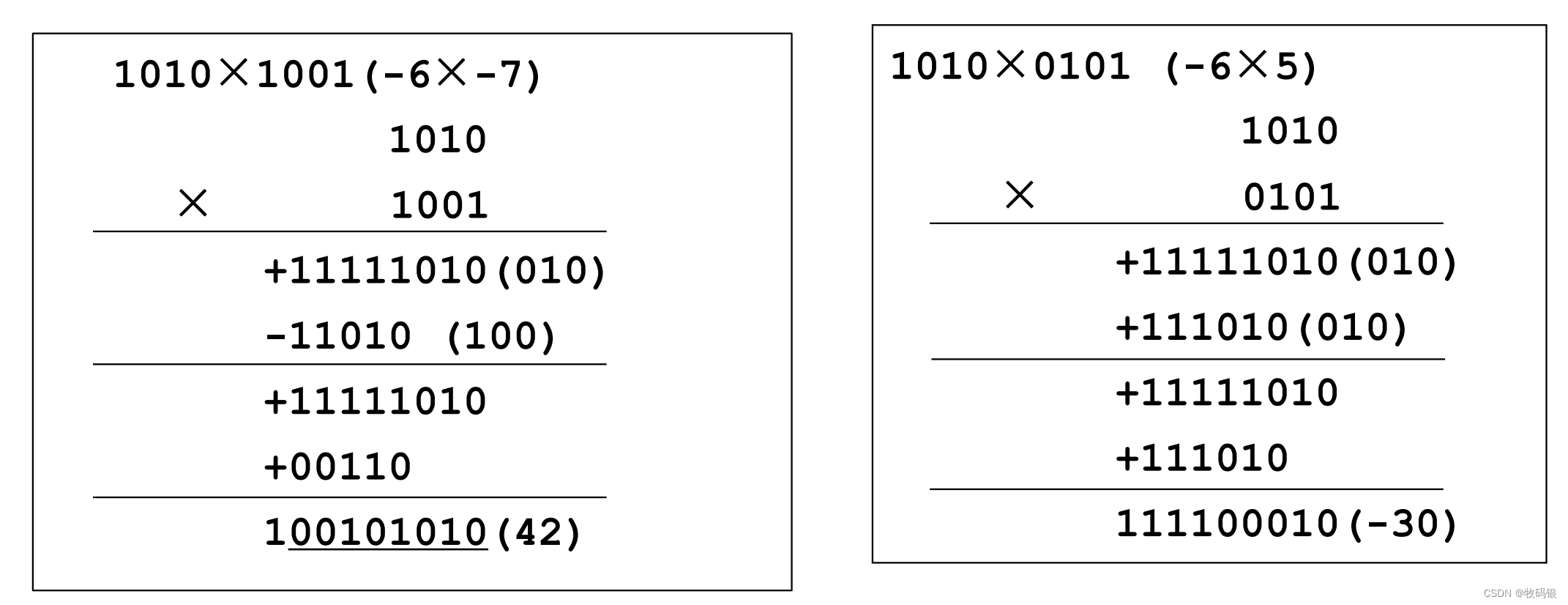
这里有几点需要注意:
1、每一次运算后是左移2位;(图16中的右边)这个地方指的是部分积的对齐;
2、加减2倍的[X]
补
_补
补时,另外再多左一1位,因为左一和乘2是等效的;(图16中的左边)
3、-[X]
补
_补
补就是“按位取反,末尾加1”
4、相加时依旧需要符号扩展后再相加
3 Booth的实现
我们知道两位Booth算法部分积一共会产生五种结果:
+[X]
补
_补
补 —— 对应的是x
i
_i
i
-[X]
补
_补
补 —— 对应的是-x
i
_{i}
i
+2[X]
补
_补
补 —— 对应的是x
i
−
1
_{i-1}
i−1
-2[X]
补
_补
补 —— 对应的是-x
i
−
1
_{i-1}
i−1
0 —— 可以不管
图17:
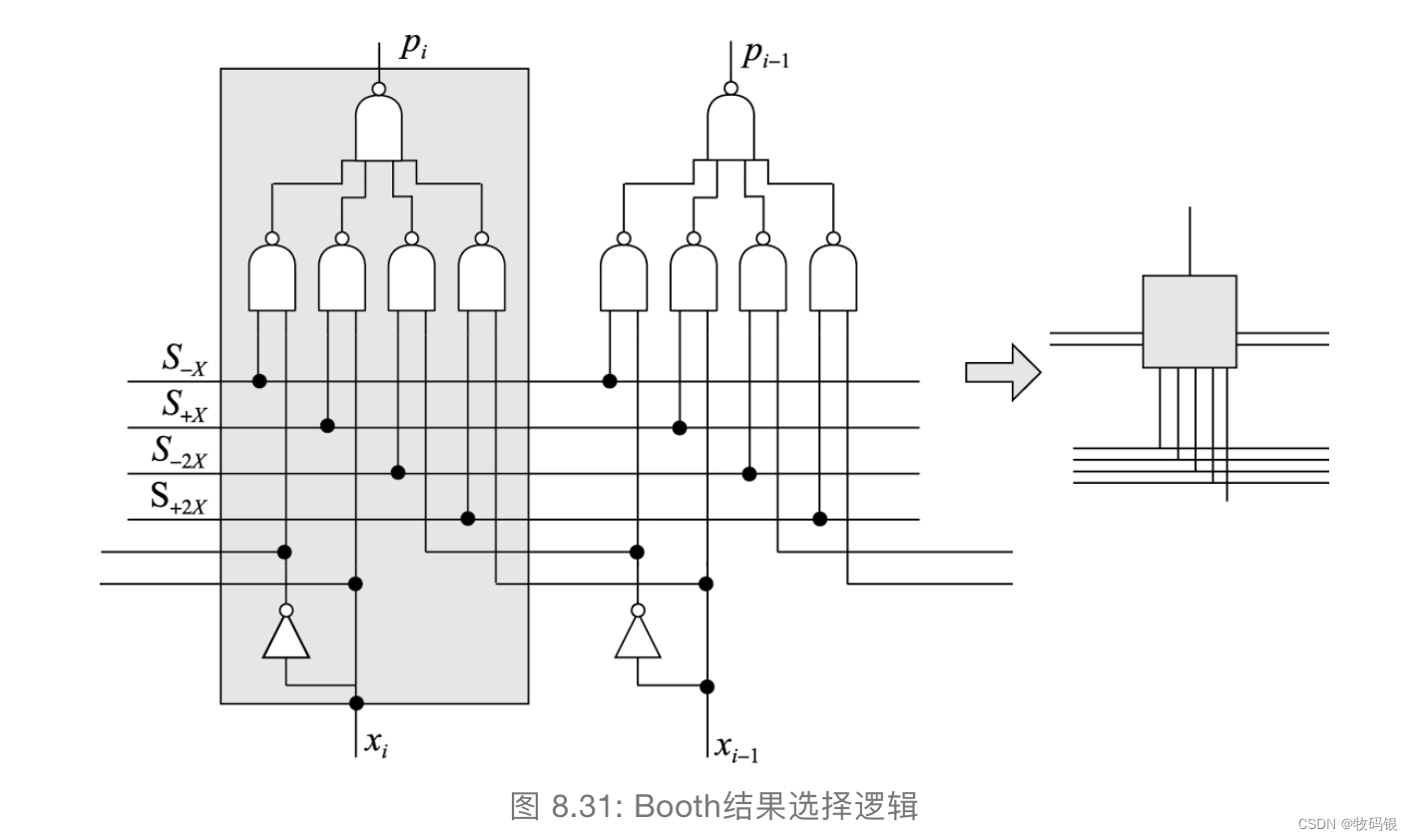
其实实现两位Booth最重要的就是选择。
图18:
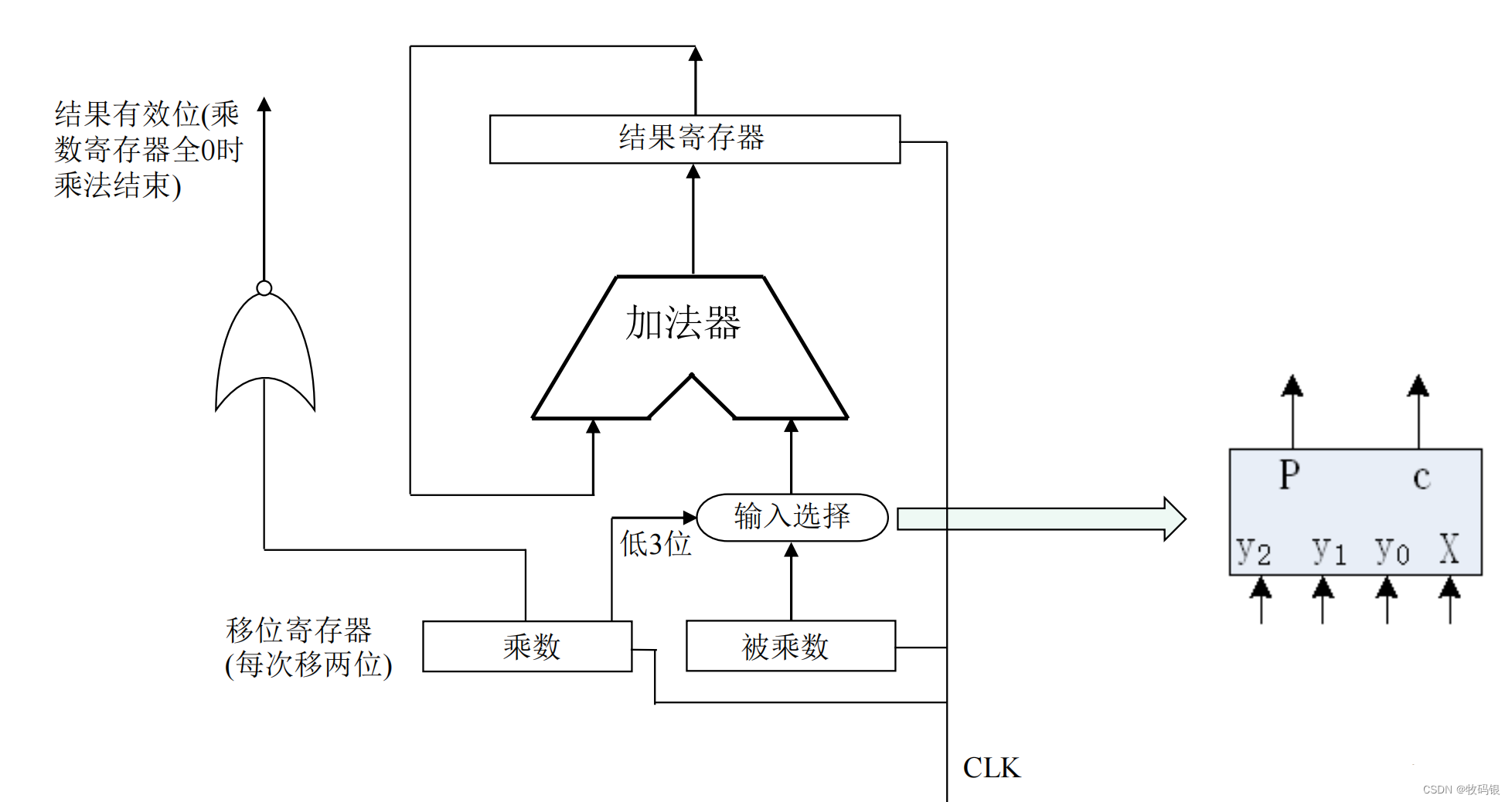
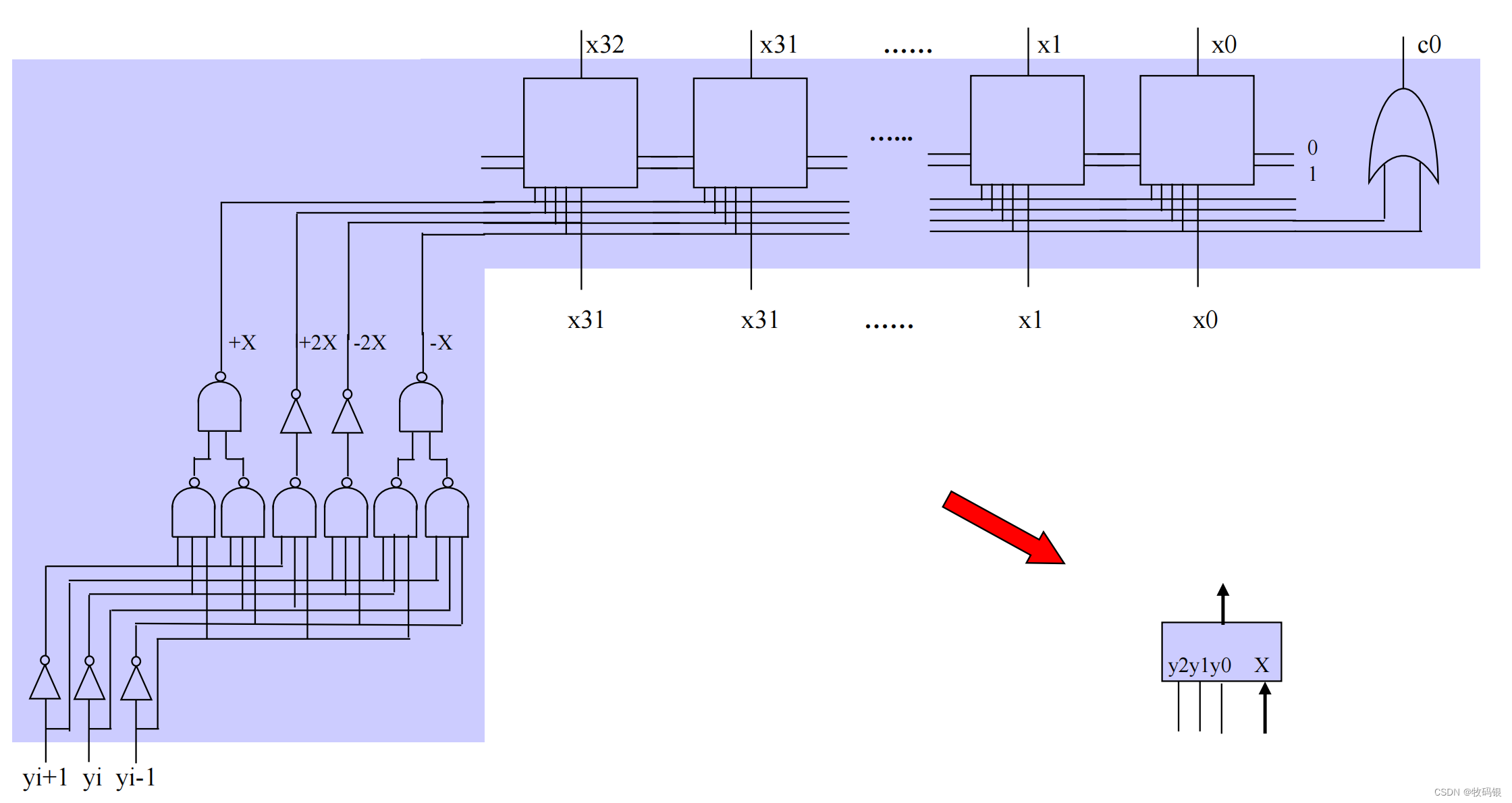
图19:
4 华莱士树(Wallace tree)
核心思想:
图20:
图21:
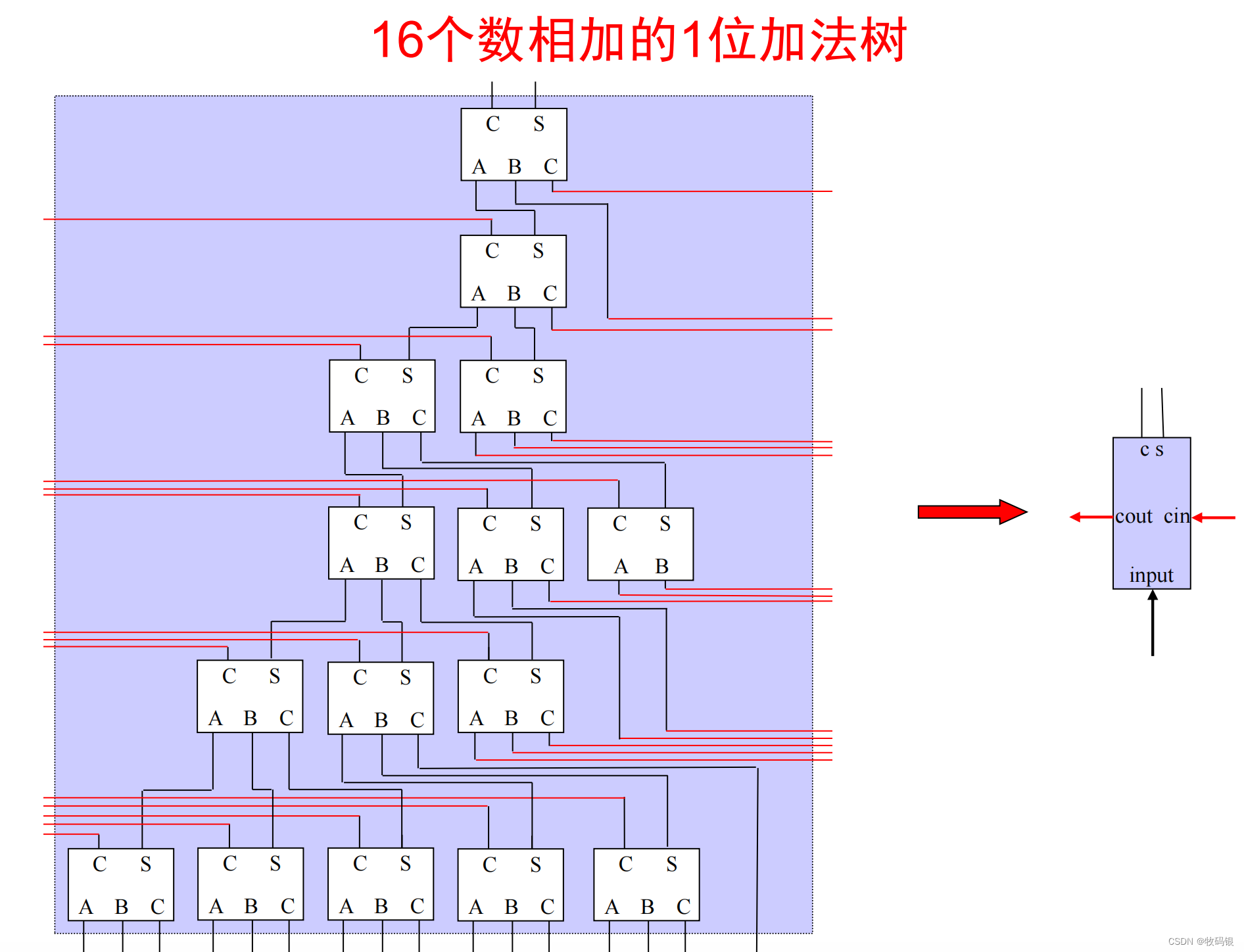
这里解释一下16个数相加的1位华莱士树,就是第一层,把16个数使用5个全加器变成11个数相加,第二层用3个全加器,把11个数变成了8个数相加,第三层使用2个全加器和1个半加器把8个数变成6个数相加,第四层用2个全加器把6个数变成4个数相加,第五层用一个全加器把4个数变成3个数相加,第六层用一个全加器把3个数变成2个数相加,然后最后可以通过一个加法器实现两个数相加便成一个数。这里只需要12级门延迟就可以完成16个数相加转换成2个数相加。
图22:
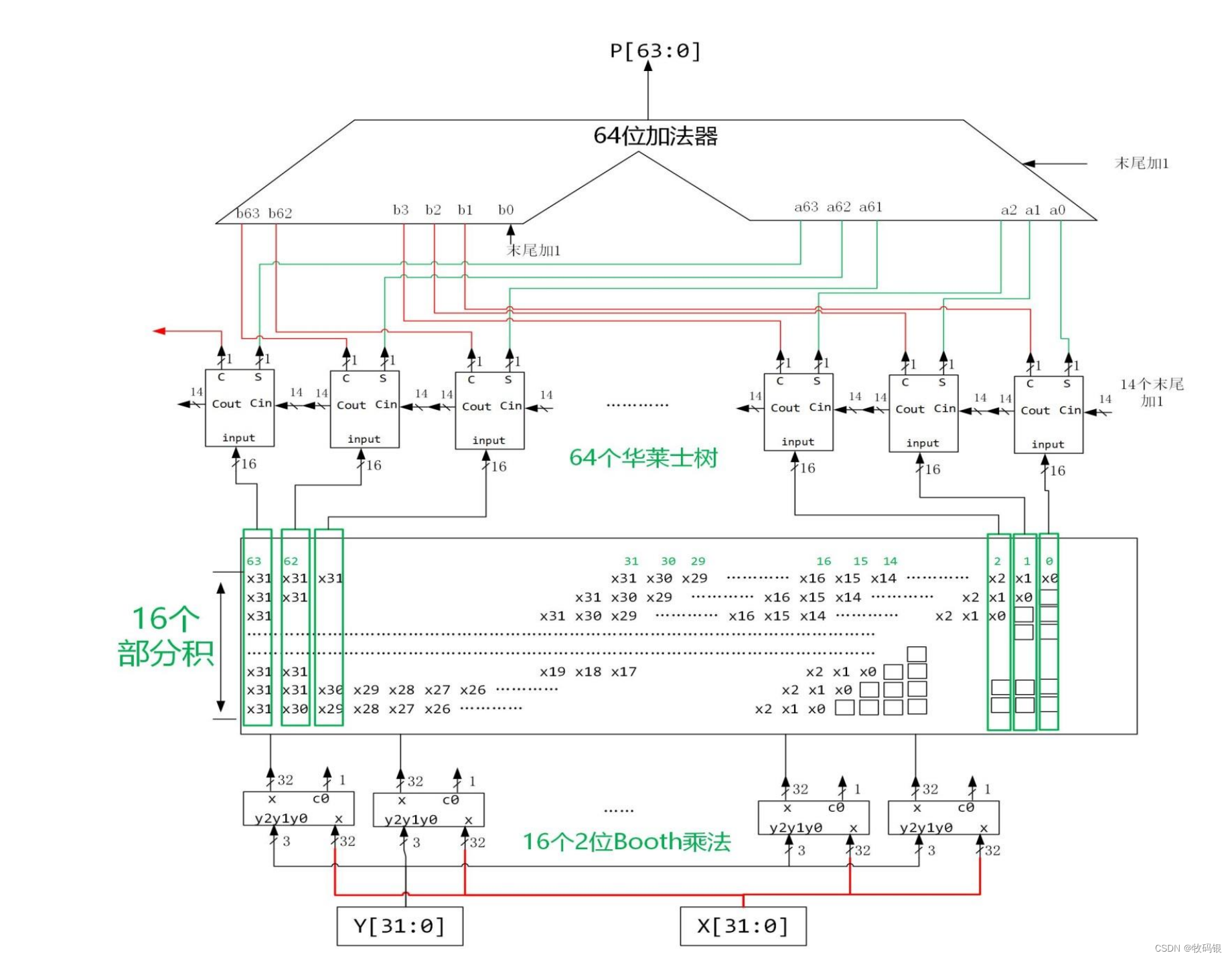
其实说简单也是比较简单的,看这幅图就比较清晰明了,两个32位数相乘。使用16个2位Booth算法形成16个部分积,再用64个1位华莱士树(这里不知道大家有没有疑问,为什么数64个?其实是因为32+32 = 64位,因为2个32位数相乘的结果是64位的),这里是把每一位的16个部分积送到一个华莱士树中,比如第0位的16个部分积送到第0棵华莱士树中;每棵华莱士树会产生两位结果,其中s是送入a中相应位,比如0号就是送入a0,但是c就要送到b中高一位,这样最后再通过一个加法器就能求出结果。
这里需要注意16个末尾加1信号的位置,图中已经注明。因为在Booth算法时加-[X] 补 _补 补和-2[X] 补 _补 补时只取反,而没有加1,所以这里需要加上。
三 、Verilog实现
实现一个16位的先行进位加法器
module add16(a, b, cin, out, cout);
input [15:0] a;
input [15:0] b;
input cin;
output [15:0] out;
output cout;
wire [15:0] p = a|b;
wire [15:0] g = a&b;
wire [3:0] P, G;
wire [15:0] c;
assign c[0] = cin;
C4 C0_3(.p(p[3:0]),.g(g[3:0]),.cin(c[0]),.P(P[0]),.G(G[0]),.cout(c[3:1]));
C4 C4_7(.p(p[7:4]),.g(g[7:4]),.cin(c[4]),.P(P[1]),.G(G[1]),.cout(c[7:5]));
C4 C8_11(.p(p[11:8]),.g(g[11:8]),.cin(c[8]),.P(P[2]),.G(G[2]),.cout(c[11:9]));
C4 C12_15(.p(p[15:12]),.g(g[15:12]),.cin(c[12]),.P(P[3]),.G(G[3]),.cout(c[15:13]));
C4 C_INTER(.p(P),.G(G),.cin(c[0]),.P(),.G(),.cout({c[12],c[8],c[4]}));
assign cout = (a[15]&b[15]) | (a[15]&c[15]) | (b[15]&c[15]);
assign out = (~a&~b&c)|(~a&b&~c)|(a&~b&~c)|(a&b&c);
endmodule
module C4(p,g,cin,P,G,cout)
input [3:0] p, g;
input cin;
output P,G;
output [2:0] cout;
assign P=&p;
assign G=g[3]|(p[3]&g[2])|(p[3]&p[2]&g[1])|(p[3]&p[2]&p[1]&g[0]);
assign cout[0]=g[0]|(p[0]&cin);
assign cout[1]=g[1]|(p[1]&g[0])|(p[1]&p[0]&cin);
assign cout[2]=g[2]|(p[2]&g[1])|(p[2]&p[1]&g[0])|(p[2]&p[1]&p[0]&cin);
endmodule
最后
以上就是唠叨小鸭子最近收集整理的关于计算机体系结构——功能部件一、功能部件——加法器二、功能部件——乘法器三 、Verilog实现的全部内容,更多相关计算机体系结构——功能部件一、功能部件——加法器二、功能部件——乘法器三内容请搜索靠谱客的其他文章。








发表评论 取消回复