文章目录
- 补码一位乘法
- 补码二位乘法
- 布斯算法的硬件实现
A.D. Booth提出了一种算法:相乘二数用补码表示,它们的符号位与数值为一起参与乘法运算的过程,直接得出用补码表示的乘法结果,且正数和负数同等对待。这种算法被称之为布斯算法。
下面讨论的都是带有符号位的数字。
补码一位乘法
补码乘法规则如下:
- 乘数的最低位增加一辅助位yn+1 = 0,下标n是从0开始,而不是从1开始。
- 判断yn-i yn-i+1的值,决定是“+X”或者“-X",或仅右移一位,得部分积。
- 重复第二步,直到最高位参见操作(y1-y0)* X,但不做位移,结果得[X*Y]补
| yn-i | yn-i+1 | |
|---|---|---|
| 1 | 0 | +[-X]补 |
| 0 | 1 | +[X]补 |
| 0 | 0 | 直接右移 |
| 1 | 1 | 直接右移 |
下面举一个例子:
- 已知 X=13,Y=-10,用布斯乘法求[X*Y]补
解:求得[X]补=01101,[Y]补=10110,[-X]补=10011,假设一个P初始化全为0,位数为两位符号位和四位有效位。

所以布斯算法的算法过程为n+1次的”判断→加减→右移“的循环,右移的次数为n次。
补码二位乘法
补码二位乘法的运算过程与布斯算法是相似的。其区别知识判断三位一组,加减运算+[X]补,+2[X]补,+2[-X]补,+[-X]补一共四种情况。每次部分积和乘数一般共同右移两位。
- 设乘数[Y]补=y0y1…yn
1.当n为偶数时,乘法运算过程中的总循环次数为n/2+1。最后一次不右移,因为最后一次是仅仅对符号位的运算。
2.当n为奇数时,乘法运算过程中的总循环次数为(n+1)/2。最后一次右移一位,因为最后一次是对符号位和最高数值位的运算,符号位的原酸不需要右移。
| yn-i-1 | yn-i | yn-i+1 | 加减规则 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | +[X]补 |
| 0 | 1 | 0 | +[X]补 |
| 0 | 1 | 1 | +2[X]补 |
| 1 | 0 | 0 | +2[-X]补 |
| 1 | 0 | 1 | +[-X]补 |
| 1 | 1 | 0 | +[-X]补 |
| 1 | 1 | 1 | 0 |
下面举个例子:
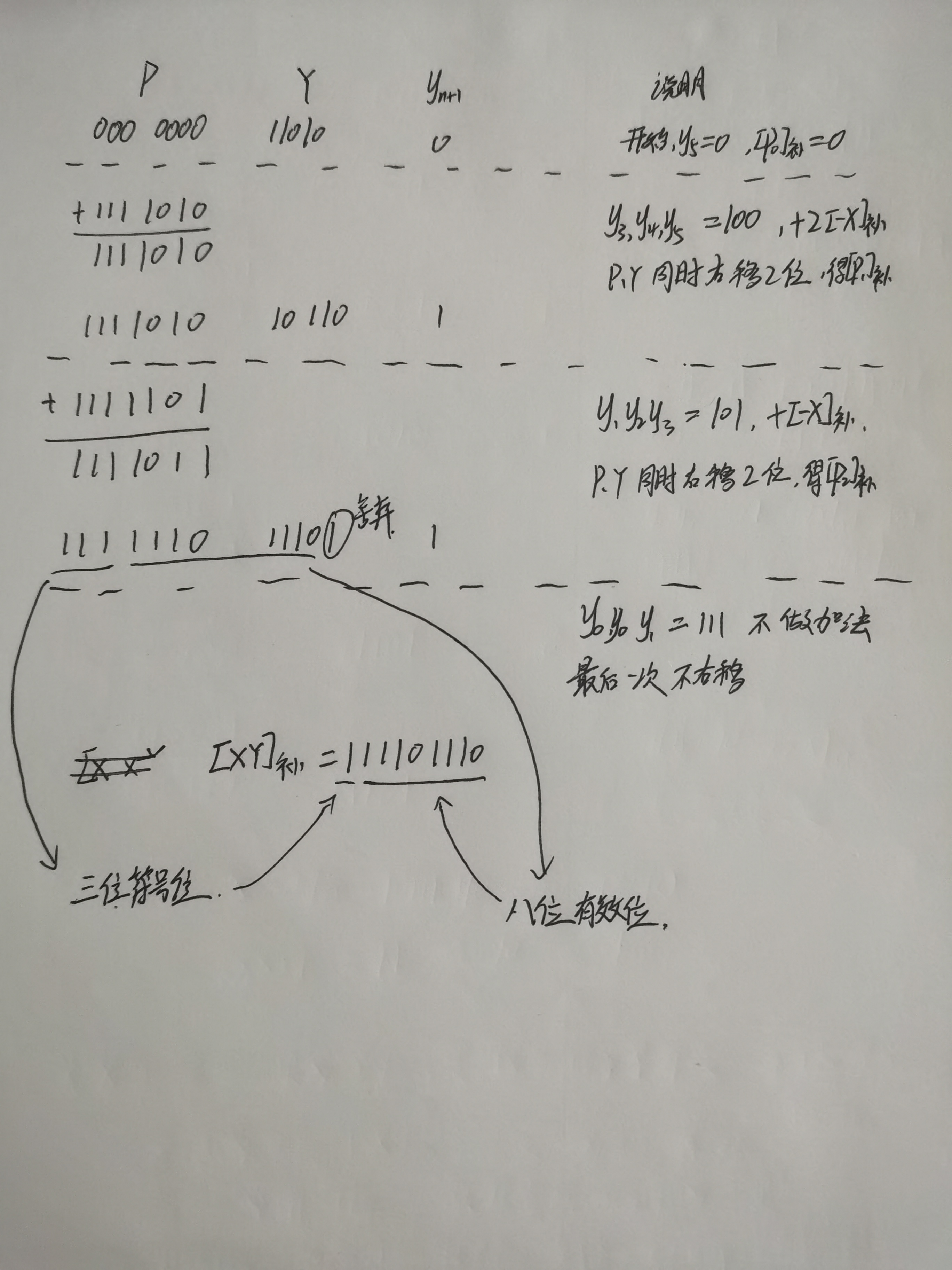
已知[X]补=00011,[Y]补=11010,则[-X]补=11101。用补码二位乘法计算[XY]补。
解:P的位数为三位符号位和四位有效位。
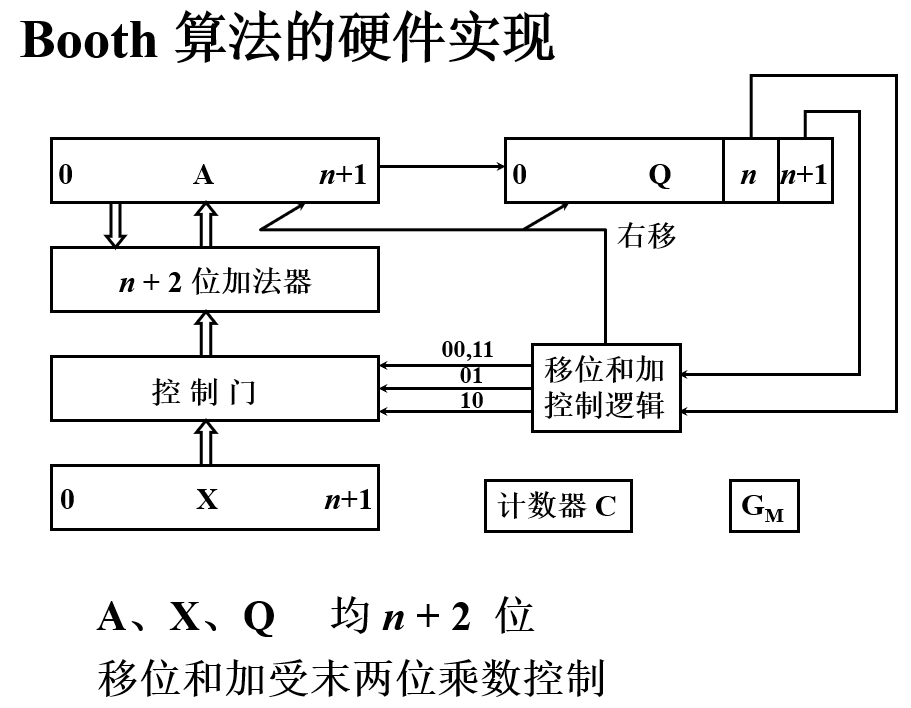
布斯算法的硬件实现
最后
以上就是细腻钢笔最近收集整理的关于补码一位乘法(Booth算法)和补码二位乘法详解补码一位乘法补码二位乘法布斯算法的硬件实现的全部内容,更多相关补码一位乘法(Booth算法)和补码二位乘法详解补码一位乘法补码二位乘法布斯算法内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复