通信原理系列文章:
通信原理之模拟幅度调制(线性调制)
通信原理之模拟角度调制(非线性调制)
通信原理之模拟调制系统信号的抗造性能
通信原理之数字调制原理
通信原理之模拟角度调制(非线性调制)详解
- 1、FM和PM
- 2、FM参数与带宽
- 2.1、调频指数和最大频偏
- 2.2、FM的频谱
- 2.3、FM带宽
- 3、FM的产生与解调
- 3.1、FM的产生
- 3.2、FM的解调(鉴频)
- 4、FM的特点与应用
正弦载波有三个参量: 幅度、频率、相位。
c ( t ) = A c o s [ w c t + ψ ] c(t)=Acos[w_ct+ψ] c(t)=Acos[wct+ψ]
这三个参量都可以用来携载消息信息 m(t) 。若 m(t) 被载在 幅度上,则为 幅度调制,AM(Amplitude Modulation);若在 频率上,则为 频率调制,简称调频 Frequncy Modulation,FM;若为 相位调制,则为 相位调制, Phase Modulation, PM。因为频率和相位是微积分的关系,故不管是调频还是调相都会是载波的角度 w c t + ψ w_ct+ψ wct+ψ 发生变化,故调频和调相统称为 角度调制。
1、FM和PM
设一般表达式为:
s m ( t ) = A c o s [ w c t + ψ ( t ) ] s_m(t)=Acos[w_ct+ψ(t)] sm(t)=Acos[wct+ψ(t)]
若幅度 A 恒定,而 ψ(t) 随消息信号 m(t) 变化,则改信号为角调信号。其中,
w
c
t
+
ψ
(
t
)
w_ct+ψ(t)
wct+ψ(t) 为已调信号的瞬时相位,ψ(t) 是相对于载波相位
w
c
t
w_ct
wct 的瞬时相位偏移,对瞬时相位求微分则可得到已调信号的瞬时角频率
w
c
+
d
ψ
(
t
)
d
t
w_c+frac{dψ(t)}{dt}
wc+dtdψ(t) ,
d
ψ
(
t
)
d
t
frac{dψ(t)}{dt}
dtdψ(t) 是相对于载频
w
c
w_c
wc 的瞬时角频偏。
若相位偏移正比于消息信号的变化规律
ψ
(
t
)
=
K
p
m
(
t
)
ψ(t)=K_pm(t)
ψ(t)=Kpm(t),则已调信号为调相信号,表达式为:
s P M ( t ) = A c o s [ w c t + K p m ( t ) ] s_{PM}(t)=Acos[w_ct+K_pm(t)] sPM(t)=Acos[wct+Kpm(t)]
其中,
K
p
K_p
Kp 为相移常数(rad/V)。
若角频偏正比于消息函数,
d
ψ
(
t
)
d
t
=
2
π
K
f
m
(
t
)
frac{dψ(t)}{dt}=2pi K_fm(t)
dtdψ(t)=2πKfm(t),而相位偏移正比于 m(t) 的积分
φ
(
t
)
=
2
π
K
f
∫
m
(
τ
)
d
τ
varphi (t)=2pi K_fint m(tau )d tau
φ(t)=2πKf∫m(τ)dτ,则已调信号为调频信号,表达式为:
s F M ( t ) = A c o s [ w c t + 2 π K f ∫ m ( τ ) d τ ] s_{FM}(t)=Acos[w_ct+2pi K_fint m(tau )d tau] sFM(t)=Acos[wct+2πKf∫m(τ)dτ]
其中,
K
f
K_f
Kf 为频偏常数 (Hz/V) ,表示单位调制电压产生的频偏量,也称调频灵敏度。
因为频率和相位是微分积分关系,故调频和调相可以相互转换。若将调制信号m(t) 通过微分器后再调频 FM,则可得到调相信号
s
P
M
(
t
)
s_{PM}(t)
sPM(t)。

调相波是频率正比于 m(t) 微分的等幅波。

若将调制信号 m(t) 经过微分器后,再调相 PM,则得到调频信号
s
F
M
(
t
)
s_{FM}(t)
sFM(t)。

调频波是频率正比于m(t) 的等幅波,其疏密随 m(t) 的大小变化。
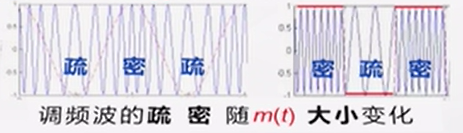
但若预先不知道消息信号 m(t) 的变化规律,不能直接判断是 PM还是 FM信号。
2、FM参数与带宽
2.1、调频指数和最大频偏
设 单音(单频正弦型信号) m ( t ) = A m c o s w m t m(t)=A_mcosw_mt m(t)=Amcoswmt,其中 w m = 2 π f m w_m=2pi f_m wm=2πfm,则有对应的角频偏为:
d ψ ( t ) d t = 2 π K f m ( t ) = 2 π K f A m c o s w m t frac{dψ(t)}{dt}=2pi K_fm(t)=2pi K_fA_mcosw_mt dtdψ(t)=2πKfm(t)=2πKfAmcoswmt
其中,
Δ
f
=
K
f
A
m
Delta f=K_fA_m
Δf=KfAm 称为最大频偏。
对应的相偏为:
ψ ( t ) = 2 π K f ∫ m ( τ ) d τ = 2 π K f A m w m s i n w m t = 2 π K f A m 2 π f m s i n w m t = Δ f f m s i n w m t ψ(t)=2pi K_fint m(tau )d tau=2pi K_f frac{A_m}{w_m}sinw_mt=2pi K_f frac{A_m}{2 pi f_m}sinw_mt=frac{Delta f}{f_m}sinw_mt ψ(t)=2πKf∫m(τ)dτ=2πKfwmAmsinwmt=2πKf2πfmAmsinwmt=fmΔfsinwmt
故,单音调频的表达式为:
s F M ( t ) = A c o s [ w c t + m f s i n w m t ] s_{FM}(t)=Acos[w_ct+m_f sinw_mt] sFM(t)=Acos[wct+mfsinwmt]
其中, m f m_f mf 称为调频指数 , m f = Δ f f m = K f A m f m m_f=frac{Delta f}{f_m}=frac{K_fA_m}{f_m} mf=fmΔf=fmKfAm,其物理含义是最大相位偏移,与调制信号的振幅 A m A_m Am 成正比,与调制频率 f m f_m fm 成反比,它涉及到 FM的传输带宽、功率分配和抗噪性能,是FM的一个重要参量。
2.2、FM的频谱
设单音调制信号为 m ( t ) = A m c o s w m t = A m c o s 2 π f m t m(t)=A_mcosw_mt=A_mcos2 pi f_mt m(t)=Amcoswmt=Amcos2πfmt,对应的单音调制FM信号的时域表达式为:
s F M ( t ) = A c o s [ w c t + m f s i n w m t ] s_{FM}(t)=Acos[w_ct+m_f sinw_mt] sFM(t)=Acos[wct+mfsinwmt]
利用三角公式展开,有
s F M ( t ) = A c o s w c t ⋅ c o s ( m f s i n w m t ) − A s i n w c t ⋅ s i n ( m f s i n w m t ) s_FM(t)=Acosw_ct cdot cos(m_fsinw_mt)-Asinw_ct cdot sin(m_fsinw_mt) sFM(t)=Acoswct⋅cos(mfsinwmt)−Asinwct⋅sin(mfsinwmt)
对两个因子分别展开成傅里叶级数:
c o s ( m f s i n w m t ) = J 0 ( m f ) + ∑ n = 1 ∞ 2 J 2 n ( m f ) c o s 2 n w m t cos(m_fsinw_mt)=J_0(m_f)+sum_{n=1}^{infty }2J_{2n}(m_f)cos2nw_mt cos(mfsinwmt)=J0(mf)+∑n=1∞2J2n(mf)cos2nwmt
s i n ( m f s i n w m t ) = 2 ∑ n = 1 ∞ J 2 n − 1 ( m f ) s i n ( 2 n − 1 ) w m t sin(m_fsinw_mt)=2sum_{n=1}^{infty }J_{2n-1}(m_f)sin(2n-1)w_mt sin(mfsinwmt)=2∑n=1∞J2n−1(mf)sin(2n−1)wmt
式中,
J
n
(
m
f
)
J_n(m_f)
Jn(mf) 为第一类 n 阶贝塞尔 (Bessel) 函数,它是调频指数
m
f
m_f
mf 的函数,
J
n
(
m
f
)
J_n(m_f)
Jn(mf) 随
m
f
m_f
mf 变化的关系曲线如下所示:
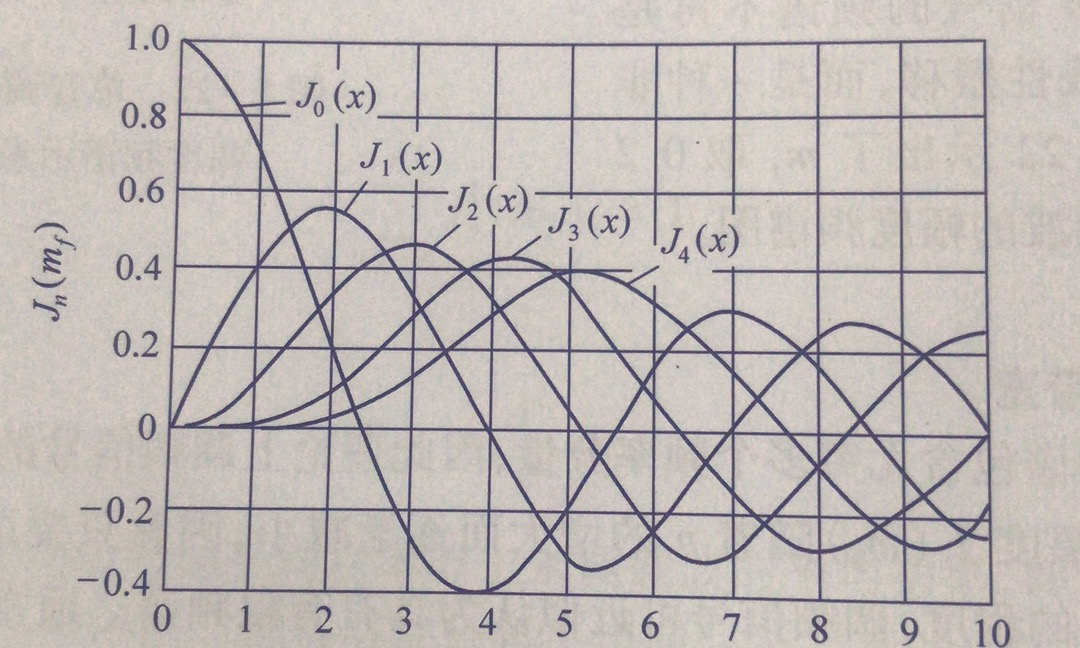
阶贝塞尔 (Bessel) 函数的主要特性为:
J
−
n
(
m
f
)
=
−
J
n
(
m
f
)
n
为
奇
数
时
J
−
n
(
m
f
)
=
J
n
(
m
f
)
n
为
偶
数
时
begin{matrix} J_{-n}(m_f)=-J_n(m_f) & n为奇数时\ J_{-n}(m_f)=J_n(m_f) & n为偶数时 end{matrix}
J−n(mf)=−Jn(mf)J−n(mf)=Jn(mf)n为奇数时n为偶数时
带入两个因子后得到FM信号的级数展开式为
s F M ( t ) = A J 0 ( m f ) c o s w c t − A J 1 ( m f ) [ c o s ( w c − w m ) t − c o s ( w c + w m ) t ] + A J 2 ( m f ) [ c o s ( w c − 2 w m ) t + c o s ( w c + 2 w m ) t ] − A J 3 ( m f ) [ c o s ( w c − 3 w m ) t + c o s ( w c + 3 w m ) t ] + . . . = A ∑ n = − ∞ ∞ J n ( m f ) c o s ( w c + n w m ) t begin{matrix} s_{FM}(t) & =AJ_0(m_f)cosw_ct-AJ_1(m_f)[cos(w_c-w_m)t-cos(w_c+w_m)t] & +\ & AJ_2(m_f)[cos(w_c-2w_m)t+cos(w_c+2w_m)t] & - \ & AJ_3(m_f)[cos(w_c-3w_m)t+cos(w_c+3w_m)t] & +... \ & =Asum_{n=-infty }^{infty }J_n(m_f)cos(w_c+nw_m)t end{matrix} sFM(t)=AJ0(mf)coswct−AJ1(mf)[cos(wc−wm)t−cos(wc+wm)t]AJ2(mf)[cos(wc−2wm)t+cos(wc+2wm)t]AJ3(mf)[cos(wc−3wm)t+cos(wc+3wm)t]=A∑n=−∞∞Jn(mf)cos(wc+nwm)t+−+...
再进行傅里叶变换,得到FM信号的频域表达式为
S F M ( w ) = π A ∑ − ∞ ∞ J n ( m f ) [ δ ( w − w c − n w m ) + δ ( w + w c + n w m ) ] S_{FM}(w)=pi Asum_{-infty }^{infty }J_n(m_f)[delta (w-w_c-nw_m)+delta (w+w_c+nw_m)] SFM(w)=πA∑−∞∞Jn(mf)[δ(w−wc−nwm)+δ(w+wc+nwm)]
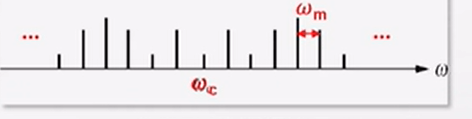
可见,调频信号FM的频谱是由载波分量
w
c
w_c
wc 和其两侧的无数边频
w
c
±
n
w
m
w_cpm nw_m
wc±nwm 组成,且频谱的幅度取决于
m
f
m_f
mf。当 n=0 时是载波分量
w
c
w_c
wc,其幅度为
A
J
0
(
m
f
)
AJ_0(m_f)
AJ0(mf) ;当 n≠0 时就是对称分布在载频两侧的边频分量
w
c
±
n
w
m
w_cpm nw_m
wc±nwm ,其幅度为
A
J
n
(
m
f
)
AJ_n(m_f)
AJn(mf) ,相邻边频之间的间隔为
w
m
w_m
wm;且当 n 为奇数时,上、下边频极性相反;当 n 为偶数时极性相同。由此可见,FM信号的频谱不再是调制信号频谱的线性搬移,而是一种非线性过程。
2.3、FM带宽
调频信号的频谱包含无穷多个频率分量,因此理论上调频信号FM的频带宽度为无限宽。但是,实际上边频幅度 J_n(m_f) 随着 n 的增大而逐渐减小,因此只要取适当的 n 值使边频分量小到可以忽略的程度,调频信号可近似认为具有有限频谱。通常采用的原则是,信号的频带宽度应包括幅度大于未调载波的 10% 以上的边频分量, 即 ∣ J n ( m f ) ∣ ≥ 0.1 |J_n(m_f)|≥0.1 ∣Jn(mf)∣≥0.1。当 m f ≥ 1 m_f ≥1 mf≥1 以后,取边频数 n = m f + 1 n=m_f+1 n=mf+1 即可。因为 n > m f + 1 n>m_f+1 n>mf+1 以上的边频幅度 J n ( m f ) J_n(m_f) Jn(mf) 均小于 0.1,这意味着大于未调载波幅度 10% 以上的边频分量均被保留。因为被保留的上、下边频数共有 2 n = 2 ( m f + 1 ) 2n=2(m_f+1) 2n=2(mf+1) 个,相邻边频之间的频率间隔为 f m f_m fm ,所以调频波的有效带宽为
B F M = 2 ( m f + 1 ) f m = 2 ( Δ f + f m ) B_{FM}=2(m_f+1)f_m=2(Delta f+f_m) BFM=2(mf+1)fm=2(Δf+fm)
这个公式称为 卡森(Carson) 公式,被广泛用于计算调频信号带宽。忽略这个频带外的分量,不会产生可察觉的失真,这个频带内保留了98%的分量。
当 调频指数
m
f
<
<
1
m_f << 1
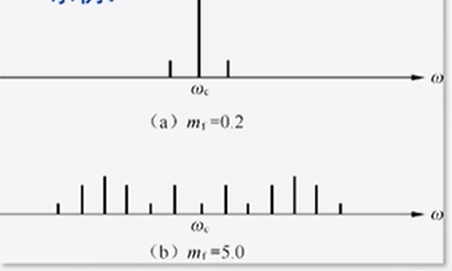
mf<<1 时,
B
F
M
≈
2
f
m
B_{FM} ≈ 2f_m
BFM≈2fm,这是窄带调频(NBFM)时的情况;
当 调频指数
m
f
>
>
1
m_f >> 1
mf>>1 时,
B
F
M
≈
2
Δ
f
B_{FM} ≈ 2Delta f
BFM≈2Δf,这是宽带调频(WBFM)时的情况;
对于多音或任意带限调制信号,FM带宽依旧可以表示为:
B F M = 2 ( m f + 1 ) f m B_{FM}=2(m_f+1)f_m BFM=2(mf+1)fm
其中, f m f_m fm 为调制信号 m(t) 的最高频率,即基带信号带宽。例如,FM广播的 Δ f = 75 k H z Delta f=75kHz Δf=75kHz ,最高调制频率为 f m = 15 k H z f_m=15kHz fm=15kHz,故调制指数 m f = Δ f f m = 5 m_f=frac{Delta f}{f_m} =5 mf=fmΔf=5, FM信号的频带宽度为:
B F M = 2 ( 5 + 1 ) x 15 = 180 k H z B_FM=2(5+1)x15=180kHz BFM=2(5+1)x15=180kHz
可见,调频信号FM的带宽比幅度已调信号的带宽要大得多。一般来说,对传输相同种类的信号,如音频信号,带宽越宽品质越高。如中波 AM 广播,其音频信号的频率 被限制的 4.5kHz, f m < 4.5 k H z f_m < 4.5kHz fm<4.5kHz,而在调频FM广播中,可将音频信号的频率扩大至 15kHz,所以调频FM电台的节目听起来要比调幅AM广播的高音丰富,清晰逼真,而调频立体声调频广播占用带宽 198kHz 则更加动听。调频方式通常用于超短波或更高频段,而不能用在中波波段。
3、FM的产生与解调
3.1、FM的产生
FM的产生分为直接法和间接法。
- 直接法,通过调制电压m(t) 控制震荡回路VCO的某个元器件,从而使振荡器的震荡频率随消息信号的规律变化。
w
i
(
t
)
=
w
0
+
K
f
m
(
t
)
w_i(t)=w_0+K_fm(t)
wi(t)=w0+Kfm(t)

其优点是:因为调制和震荡合二为一,故电路简单,可获得较大频偏。缺点是:稳定度不高。通常采用锁相环PLL调频器进行改进。
- 间接法,是利用调相的方法实现调频的。原理是,对 m(t) 进行积分、调相产生 窄带调频 NBFM,经倍频以后输出 宽带调频 WBFM。
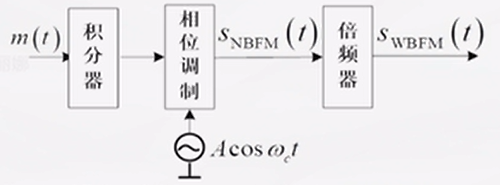
其优点是:频率稳定度好。缺点是电路较复杂,需要多次倍频和混频。
3.2、FM的解调(鉴频)
鉴频器有多种形式,这里主要介绍振幅鉴频器,它的核心电路是 微分电路和包络检波,微分电路将幅度恒定的调频波
s
F
M
(
t
)
s_FM(t)
sFM(t) 变换成幅度和频率都随信号 m(t) 变化的调频调幅波
s
d
(
t
)
s_d(t)
sd(t)。
s
F
M
(
t
)
=
A
c
o
s
[
w
c
t
+
K
f
∫
m
(
τ
)
d
τ
]
s_{FM}(t)=Acos[w_ct+K_fint m(tau) d tau]
sFM(t)=Acos[wct+Kf∫m(τ)dτ]
d
d
(
t
)
=
−
A
[
w
c
+
K
f
m
(
τ
)
]
s
i
n
[
w
c
t
+
K
f
∫
m
(
τ
)
d
τ
]
d_d(t)=-A[w_c+K_fm(tau)]sin[w_ct+K_fint m(tau) d tau]
dd(t)=−A[wc+Kfm(τ)]sin[wct+Kf∫m(τ)dτ]
这个变换实际上是将调频波中隐含在频率变化中的 m(t),浮出到表面即幅度上,故可以采用包络检波器将
s
d
(
t
)
s_d(t)
sd(t) 信号中的包络
A
[
w
c
+
K
f
m
(
τ
)
]
A[w_c+K_fm(tau)]
A[wc+Kfm(τ)] 检出,然后通过低通隔掉直流分量 A,就可以还原原来的调制信号
m
o
(
t
)
=
K
d
K
f
m
(
t
)
m_o(t)=K_dK_fm(t)
mo(t)=KdKfm(t) 。
4、FM的特点与应用
FM的特点:
- 包络恒定,这是不同于AM的重要特点。FM将消息隐含在频率上而不是幅度上。
- 抗噪声能力强。由于各种噪声干扰的作用主要表现在信号的振幅上,所以解调时可以通过限幅器来消除这种干扰。
- FM的频偏正比于m(t) d ψ ( t ) d t = 2 π K f m ( t ) frac{dψ(t)}{dt}=2pi K_fm(t) dtdψ(t)=2πKfm(t),相偏正比于 m(t) 的积分 ψ ( t ) = 2 π K f ∫ m ( τ ) d τ ψ(t)=2pi K_f int m(tau) d tau ψ(t)=2πKf∫m(τ)dτ。
- FM的带宽比AM大 ( m f + 1 ) (m_f+1) (mf+1) 倍, B F M = 2 ( m f + 1 ) f m B_{FM}=2(m_f+1)f_m BFM=2(mf+1)fm, m f = Δ f f m m_f=frac{Delta f}{f_m} mf=fmΔf,也正因此FM需占用较大的信道带宽,频谱利用率低。
FM的应用:
- 主要应用在高质量或信道噪声大的场合,如调频广播,电视伴音、卫星通信、移动通信、微波通信和蜂窝电话等。
例:设某角调波的表达式为:
s
m
(
t
)
=
8
c
o
s
(
2
×
1
0
6
π
t
+
10
c
o
s
2000
π
t
)
s_m(t)=8cos(2×10^6 pi t + 10 cos 2000 pi t)
sm(t)=8cos(2×106πt+10cos2000πt)
可知,幅度 A=8 ,载波角频率
w
c
=
2
×
1
0
6
π
w_c=2×10^6 pi
wc=2×106π,调制角频率
w
c
=
2000
π
w_c=2000 pi
wc=2000π,调制频率
f
m
=
w
m
2
π
=
1000
fm=frac{w_m}{2pi}=1000
fm=2πwm=1000,则可以得到
(1)已调波的功率为:
p
=
A
2
2
p=frac{A^2}{2}
p=2A2
由已调信号的瞬时相位偏移
10
c
o
s
2000
π
t
10cos2000pi t
10cos2000πt 可得 最大相位偏移为
Δ
θ
=
10
r
a
d
Delta θ=10 rad
Δθ=10rad;
最大频偏
Δ
f
=
w
m
2
π
=
ψ
(
t
)
d
t
2
π
=
10
×
2000
π
2
π
=
10
k
H
z
Delta f = frac{w_m}{2pi} =frac{frac{ψ(t)}{dt}}{2 pi}=frac{10×2000pi}{2pi}=10kHz
Δf=2πwm=2πdtψ(t)=2π10×2000π=10kHz;
调频指数
m
f
=
Δ
f
f
m
=
10
×
1
0
3
1
0
3
=
10
m_f=frac{Delta f}{f_m}=frac{10×10^3}{10^3}=10
mf=fmΔf=10310×103=10,调频指数是最大相位偏移的概念,等于
Δ
θ
Delta θ
Δθ。
带宽:
B
F
M
=
2
(
m
f
+
1
)
f
m
=
2
(
10
+
1
)
×
10
=
220
B_{FM}=2(m_f+1)f_m=2(10+1)×10=220
BFM=2(mf+1)fm=2(10+1)×10=220
B
P
M
=
2
(
Δ
θ
+
1
)
f
m
=
2
(
10
+
1
)
×
10
=
220
B_{PM}=2(Delta θ+1)f_m=2(10+1)×10=220
BPM=2(Δθ+1)fm=2(10+1)×10=220
(2)是FM信号还是PM信号呢?无法判断,因为不知道消息信号m(t)的变化规律。
(3)若是FM信号,且
K
f
=
2000
H
z
/
V
K_f=2000Hz/V
Kf=2000Hz/V ,则根据
d
ψ
(
t
)
d
t
=
2
π
K
f
m
(
t
)
frac{dψ(t)}{dt}=2pi K_fm(t)
dtdψ(t)=2πKfm(t),可得到
m
(
t
)
=
10
×
2000
π
s
i
n
(
2000
π
t
)
2
π
K
f
=
5
s
i
n
(
2000
π
t
)
m(t)=frac{10×2000pi sin(2000pi t)}{2pi K_f}=5sin(2000pi t)
m(t)=2πKf10×2000πsin(2000πt)=5sin(2000πt)。
(4)若是PM信号,且
K
P
=
4
r
a
d
/
V
K_P=4 rad/V
KP=4rad/V ,则根据
ψ
(
t
)
=
K
P
m
(
t
)
ψ(t)=K_P m(t)
ψ(t)=KPm(t) ,可得
m
(
t
)
=
ψ
(
t
)
K
P
=
10
c
o
s
(
2000
π
t
)
4
=
2.5
c
o
s
(
2000
π
t
)
m(t)=frac{ψ(t)}{K_P}=frac{10cos(2000pi t)}{4}=2.5cos(2000pi t)
m(t)=KPψ(t)=410cos(2000πt)=2.5cos(2000πt) 。
本文为个人学习笔记,欢迎一起学习讨论。
最后
以上就是土豪墨镜最近收集整理的关于通信原理之模拟角度调制(非线性调制)详解1、FM和PM2、FM参数与带宽3、FM的产生与解调4、FM的特点与应用的全部内容,更多相关通信原理之模拟角度调制(非线性调制)详解1、FM和PM2、FM参数与带宽3、FM内容请搜索靠谱客的其他文章。








发表评论 取消回复