通信原理期末复习笔记 -- 第五章 模拟调制系统

模拟调制系统

调制就是把信号形式转换成适合在信道中传输的一种过程。广义的调制分为基带调制和带通调制（即载波调制）。
调制的作用和目的：1. 把基带信号频谱搬移到交高的频率上，就可以提高发射效率。2. 把多个基带信号搬移到不同频带处，以实现信道的多路复用，提高信道的利用率。3. 扩展信号带宽提高系统的抗干扰能力。

1. 幅度调制原理

1.1 AM调制

时域表达式：
$$\begin{array}{rl}{s}_{\mathrm{A}\mathrm{M}}(t)=& \left[A_0+m(t)\right]\cos {\omega }_{c}t=\\ & A_0\cos {\omega }_{c}t+m(t)\cos {\omega }_{\mathrm{c}}t\end{array}$$
A₀为外加直流分量，m(t)为调制信号。

频域表达式:
$$S_{AM}(\omega )=\pi A_0\left[\delta \left(\omega +{\omega }_c\right)+\delta \left(\omega -{\omega }_c\right)\right]+\frac{1}{2}\left[M\left(\omega +{\omega }_c\right)+M\left(\omega -{\omega }_c\right)\right]$$

当满足条件

$${|m(t)|}_{\max }⩽A_0$$
时，不会出现过调幅现象。

带宽： B_AM = 2f_H (f_H为基带信号带宽)

平均功率：
$$\begin{array}{rl}{P}_{AM}& =\overline{s_{AM}^2(t)}=\overline{{\left[A_0+m(t)\right]}^2{\cos }^2{\omega }_{c}t}\\ & =\overline{A_0^2{\cos }^2{\omega }_{c}t}+\overline{m^2(t){\cos }^2{\omega }_{c}t}+\overline{2A_{0}m(t){\cos }^2{\omega }_{c}t}\end{array}$$

通常调制信号的平均值为0，即 m(t) = 0,则

$$\begin{gathered} P_{\mathrm{A}\mathrm{M}}=\frac{A_0^2}{2}+\frac{\overline{m^2(t)}}{2}=P_{\mathrm{c}}+P_s \\ 载波功率：P_c=A_0^2/2 \\ 边带功率：P_x=\overline{m^2(t)}/2 \end{gathered}$$

调制效率为：

$${\eta }_{\mathrm{A}\mathrm{M}}=\frac{P_{\mathrm{s}}}{P_{\mathrm{A}\mathrm{M}}}=\frac{\overline{m^2(t)}}{A_0^2+m^2(t)}$$
在“满调幅”（|m(t)_max|=A₀。时，也称100%调制）条件下，这时调制效率的最大值为${\eta }_{\mathrm{A}\mathrm{M}}$=1/3。因此，AM信号的功率利用率比较低。

优点：系统结构简单，成本低，至今仍然用于无线电广播。

1.2 双边带调制（DSB）

时域表达式：
$$S_{\mathrm{D}\mathrm{S}\mathrm{B}}(t)=m(t)\cos {\omega }_{c}t$$

频域表达式：
$$S_{\mathrm{D}\mathrm{S}\mathrm{B}}(\omega )=\frac{1}{2}\left[M\left(\omega +{\omega }_c\right)+M\left(\omega -{\omega }_c\right)\right]$$

幅度较原信号减半

优点： DSB调制的效率是100%，全部功率用于信息传输。但是DSB信号的两个边带中的任意一个都包含了$M(\omega )$的所有频谱成分，因此只需要传输其中一个边带即可。

1.3 单边带调制（SSB）

产生单边带信号的方法有：滤波法和相移法

滤波法：
高通滤波器：
$$H(\omega )=H_{\mathrm{U}\mathrm{S}\mathrm{B}}(\omega )=\{\begin{array}{ll}1& |\omega |>{\omega }_{\mathrm{c}}\\ 0& |\omega |⩽{\omega }_{\mathrm{c}}\end{array}$$

低通滤波器：
$$H(\omega )=H_{\mathrm{L}\mathrm{S}\mathrm{B}}(\omega )=\{\begin{array}{ll}1& |\omega |<{\omega }_{\mathrm{c}}\\ 0& |\omega |⩾{\omega }_{\mathrm{c}}\end{array}$$

则SSB信号可以表示为：
$$S_{\mathrm{S}\mathrm{S}\mathrm{B}}(\omega )=S_{\mathrm{U}\mathrm{S}\mathrm{B}}(\omega )\cdot H(\omega )$$

缺点：所需要的边带滤波器太理想，难以实现。

相移法：

设单频调制信号为
$$m(t)=A_m\cos {\omega }_{m}t$$
载波为
$$c(t)=\cos {\omega }_{c}t$$
则DSB信号的时域表达式为
$$S_{DSB}=A_m\cos {\omega }_m\cos {\omega }_c=\frac{1}{2}{A}_m\cos ({\omega }_c+{\omega }_m)+\frac{1}{2}{A}_m\cos ({\omega }_c-{\omega }_m)$$

保留上边带：

$$S_{USB}=\frac{1}{2}{A}_m\cos ({\omega }_c+{\omega }_m)=\frac{1}{2}{A}_m\cos {\omega }_{c}t\cos {\omega }_{m}t-\frac{1}{2}{A}_m\cos {\omega }_{c}t\cos {\omega }_{m}t$$

保留下边带：
$$S_{LSB}=\frac{1}{2}{A}_m\cos ({\omega }_c-{\omega }_m)=\frac{1}{2}2A_m\cos {\omega }_{c}t\cos {\omega }_{m}t+\frac{1}{2}{A}_m\sin {\omega }_{c}t\sin {\omega }_{m}t$$

希伯尔变换：
由于
$$A_m\hat{\cos }{\omega }_{m}t=A_m\sin {\omega }_{m}t$$
则
$$S_{SSB}=1/2A_m\cos {\omega }_{m}t\cos {\omega }_{c}t\mp 1/2A_m\hat{\cos }{\omega }_{m}t\sin {\omega }_{c}t$$
当调制信号为任意信号时
$$S_{SSB}=\frac{1}{2}m(t)\cos {\omega }_{c}t\mp \frac{1}{2}\hat{m}(t)\sin {\omega }_{c}t$$
其中$\hat{m}(t)$为m(t)的希伯尔变换。即将m(t)相移π/2。

优点：相移法利用相移网络对载波或者调制信号进行适当的相移，以便在合成过程中间其中的一个边带抵消而获得SSB信号。相移法不需要滤波器具有陡峭的截止特性，不论载频有多高，都可以一次实现SSB调制。频带宽度低、可以节省发射功率。

缺点：难以实现精确的相移π/2；实现起来较其他调幅方式更复杂；不能直接反映调制信号的变化，仍然需要相干解调。

1.4 残留边带调制

残留边带（VSB）调制是介于SSB与DSB之间的一种折中方式，它既克服了DSB信号占用频带宽的缺点，又解决了SSB信号实现中的困难。在这种调制方式中，不像SSB中那样完全抑制DSB信号的一个边带，而是逐渐切割，使其残留一小部分，如图所示。

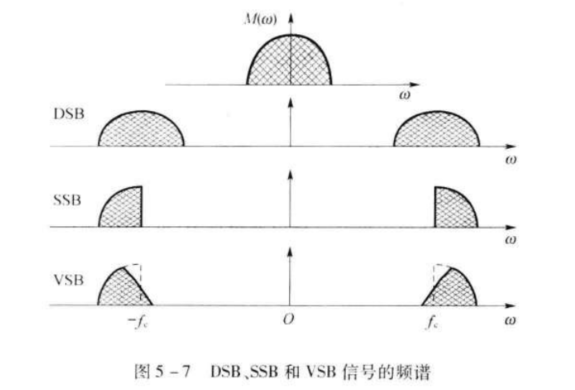
残留边带滤波器的传输特性H(w)必须满足的条件是：$H(\omega -{\omega }_c)+H(\omega -{\omega }_c)=常数，|\omega |<{\omega }_H$,该条件的含义是：残留边带滤波器的特性H(w)在$\pm {\omega }_c$处必须具有互补对称（奇对称）特性（如下图中的虚线），相干解调才能无失真的从残留边带中恢复所需要的调制信号。

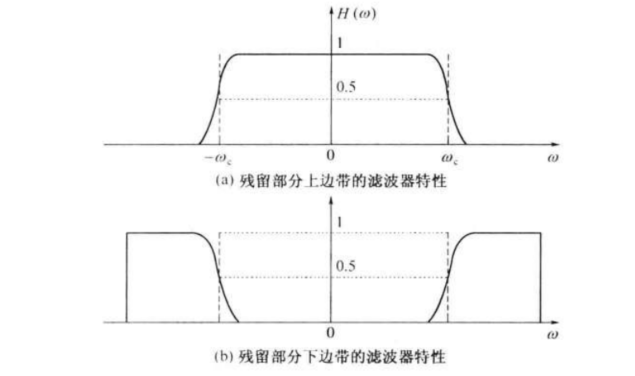
（1）VSB既克服了DSB信号占用频带宽的缺点，又解决了SSB信号实现上的难题。
（2）调制效率100%；带宽介于SSB与DSB之间，即f_H<B_VSB<2f_H。
（3）VSB广泛用在电视广播系统中的图像信号传输。这是因为电视图像信号的低频分量丰富，且占有0~
6MHz的频带范围，所以不便采用SSB或DSB。

1.5 相干解调与包络检波

a.相干解调

相干解调的一般模型如下图所示：

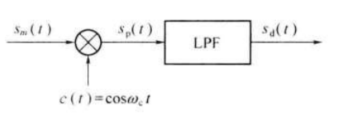
相干解调时，为了无失真的恢复原基带信号，接收端必须提供一个与接收的已调信号载波同频同相的本地载波（相干载波），它与接收的已调信号相乘后，经过低通滤波器取出低频分量，即可得到原始的基带信号。

b.包络检波

包络检波器通常有半波或全波整流器和低通滤波器组成。属于非相干解调。如下图为二极管峰值包络检波器。

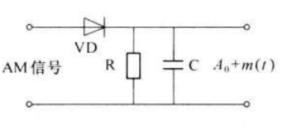
RC需要满足的条件为 $f_H\ll \frac{1}{RC}\ll f_c$

其中：f_H为调制信号的最高频率，f_c为载波频率。

满足上式的条件下，检波器的输出为：A₀+m(t)， 隔去直流A₀后即可得到原信号m(t)。

2 线性调制的抗噪声性能

2.1 分析模型

解调器抗噪声性能分析模型：

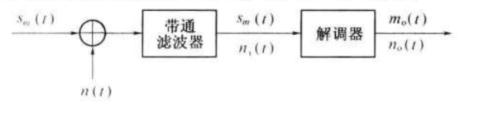
图中，S_m(t)为已调信号，n(t)为信道加性高斯白噪声（零均值），BPF为带通滤波器，作用是滤除信号频道外的噪声，n_i(t)是n(t)经过BPF后形成的窄带高斯噪声.

若白噪声n(t)的单边功率谱密度为n₀，BPF是高度为1、带宽为B的理想矩形函数，则解调器输入噪声n_i（t）的功率为

$$N_i=n_{0}B$$

模拟通信系统的抗噪声性能指标———输出信噪比：
$$\frac{S_o}{N_o}=\frac{解调器输出有用信号的平均功率}{解调器输出噪声的平均功率}=\frac{\overline{m_0^2(t)}}{\overline{n_o^2(t)}}$$
信噪比增益：用于比较同类调制系统采用不同解调器时的性能
$$G=\frac{S_o/N_o}{S_i/N_i}$$

输入信噪比：
$$\frac{S_o}{N_o}=\frac{解调器输入已调信号的平均功率}{解调器输入噪声的平均功率}=\frac{\overline{m_0^2(t)}}{\overline{n_o^2(t)}}$$

2.2 DSB调制系统的性能

DSB相干解调抗噪声性能分析模型：

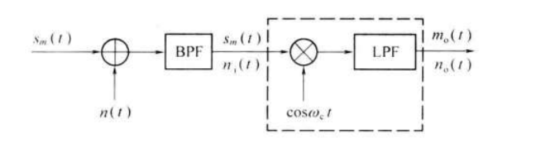
输入信噪比为：

$$\frac{S_i}{N_i}=\frac{\frac{1}{2}\overline{m^2(t)}}{n_{0}B}$$

输出信噪比为：

$$\frac{S_o}{N_o}=\frac{\overline{m^2(t)}}{n_{0}B}$$

制度增益为：

$$G_{DSB}=\frac{S_0/N_0}{S_i/N_i}=2$$

2.3 SSB调制系统的性能

输入信噪比为：

$$\frac{S_i}{N_i}=\frac{\frac{1}{4}\overline{m^2(t)}}{n_{0}B}=\frac{\overline{m^2(t)}}{4n_{0}B}$$

输出信噪比为：

$$\frac{S_o}{N_o}=\frac{\frac{1}{16}\overline{m^2(t)}}{\frac{1}{4}{n}_{0}B}=\frac{\overline{m^2(t)}}{4n_{0}B}$$
制度增益为：

$$G_{SSB}=\frac{S_0/N_0}{S_i/N_i}=1$$

对比DSB和SSB：

• 由上列公式可知，G_DSB = 2G_SSB，能否说明DSB系统抗噪声性能比SSB好呢？
  答:不能，因为两者的输入信号功率不同、带宽不同，在相同的噪声功率谱密度n₀条件下，输入噪声功率也不同，所以两者的输出信噪比是在不同条件下得到的。如果我们在相同的输入信号功率S_i，相同的输入噪声功率谱密度n₀，相同的基带信号带宽f_H条件下，对这两种调制方式进行比较，可以发现它们的输出信噪比是相等的。这就是说，两者的抗噪声性能是相同的。但SSB所需的传输带宽仅是DSB的1/2，因此SSB得到普遍应用。

要点：

• DSB的制度增益为2，即输出信噪比是输入信噪比的2倍，表示信噪比改善了一倍，原因是相干解调把噪声中的正交分量抑制调，从而使得噪声功率减半。
• SSB的制度增益为1。这是因为SSB信号和噪声有相同表示形式（同相和正交），在相干解调过程中，信号和噪声的正交分量均被抑制掉，所以信噪比没有改善。
• 近似认为VSB的抗噪声性能等于SSB。

2.4 AM包络检波的性能

AM包络检波的抗噪声性能分析模型：

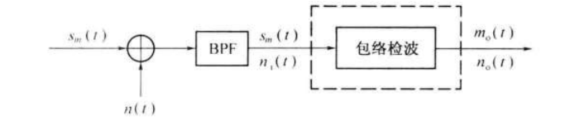
设解调器的输入信号为：
$$S_m(t)=[A_0+m(t)]\cos {\omega }_{c}t$$
输入信噪比为：

$$\frac{S_i}{N_i}=\frac{A_0^2+\overline{m^{2}t}}{2n_{0}B}$$

大信噪比下输出信噪比为：
$$\frac{S_0}{N_0}=\frac{\overline{m^2(t)}}{n_{0}B}$$

讨论：（1）对于100%调制（即A=Im（t）Imax），且m（t）是单频正弦信号时，AM的最大信噪比增益为G_AM = 2/3；
（2）大信噪比时，AM包络检波时的性能与相干解调时的性能几乎一样。但相干解调时的G不受信号与噪声相对幅度假设条件的限制。

小信噪比时：
检波输出E（t）中没有单独的信号项，有用信号m（t）被噪声扰乱。这时，输出信噪比不是按比例地随着输入信噪比下降，而是急剧恶化，这种现象称为解调器的门限效应。开始出现门限效应的输入信噪比称为门限值。这种门限效应是由包络检波器的非线性解调作用所引起的。

3 非线性调制（角度调制）原理

频率调制：在调制时，载波的频率随调制信号的频率变化。

角度调制：载波的相位随调制信号的相位变化而变化。

角度调制是非线性调制，而幅度调制是线性调制。

与幅度调制相比，优点是：较高的抗噪声性能。缺点是占用更宽的带宽。

3.1 角度调制的基本概念

3.1.1 FM和PM信号的一般表达式

角度调制信号的一般表达式为：
$$S_m(t)=A\cos [{\omega }_{c}t+\varphi (t)]$$
其中：

A为载波的恒定振幅；

${\omega }_{c}t+\varphi (t)$为信号的瞬时相位；

$d[{\omega }_{+}c+\varphi (t)]$为瞬时角频率。即为$omega(t)$;

$d\varphi (t)/d(t)$为瞬时频偏。

相位调制：是指损失相位便宜随调制信号m(t)作线性变化。

相位偏移：

$$\varphi (t)=k_{p}m(t)$$

调相信号为：
$$S_{pm}(t)=Acos({\omega }_{c}t+K_{p}m(t))$$

其中K_p为调相灵敏度。

$$\frac{d\varphi (t)}{dt}=k_{f}m(t)$$

k_f为调频灵敏度，这时的相位偏移为：
$$\varphi (t)=k_f$$

调频信号为：

$$S_{fm}=A\cos ({\omega }_{c}t+K_{f}m())$$

3.1.2 单音调制FM与PM

设调制信号为单一的正弦波，即
$$m(t)=A_m\cos {\omega }_{m}t$$

对载波进行相位调制得到PM信号：

$$S_{pm}=A_m\cos ({\omega }_{c}t+m_p\cos {\omega }_{m}t)$$
m_p = K_pA_m为调制指数。表示最大的相位偏移。

对载波进行频率调制得到FM信号：

$$S_{FM}(t)=A_m\cos ({\omega }_{c}t+m_f\sin {\omega }_{m}t)$$

m_f为调频指数。

$$m_f=\frac{k_f{A}_m}{{\omega }_m}=\frac{\Delta \omega }{{\omega }_m}=\frac{\Delta f}{f_m}$$

表示最大相移偏移，其中最大角频偏为$\Delta \omega =k_f{A}_m$,最大频偏为$\Delta f=m_f\cdot f_m$。

3.1.3 FM与PM的关系

间接调相：调制信号先微分后调频，得到调相波。

间接调频：调制信号先积分后调相，得到调频波。

3.2 窄带调频

当 FM 信号的最大瞬时相位满足

$$|K_f\int m(\tau )d\tau |<<\frac{\pi }{6}(或0.5)$$

时，FM的频宽比较窄，称为窄带调频，当上式不满足时为宽带调频。

AM与NBFM的本质区别：在AM中，两边频的合成矢量与载波相同，所以只有幅度的变化，无相位的变化；在NBFM中，由于下边频为负，两个边频的合成矢量则是正交相加，所以NBFM不仅有相位的变化，幅度也有少量的变化，当最大相位偏移满足上式，幅度基本不变。

AM调制的带宽与NBFM的带宽相同。

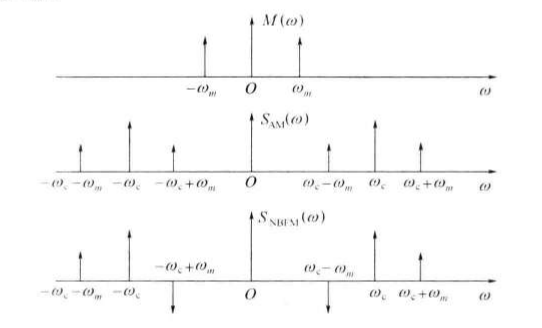
NBFM的时域表达式为：

$$S_{NBFM}=A\cos {\omega }_{c}t-[A{K}_f\int m(\tau )d\tau ]sin{\omega }_{c}t$$

频域表达式为：

3.3 宽带调频

调频信号的带宽（卡森公式）：

$$B_{FM}=2(m_f+1)f_m=2(\Delta f+f_m)$$

当m_f <<1 时，$B_{FM}=2f_m(NBFM)$; 带宽由第一对边频分量f_m决定。

当m_f >> 1时，$B_{FM}=2\Delta f(WBFM)$; 带宽由最大频偏$\Delta f$决定。

多音或任意带限信号调制时的调制信号的带宽也可以用卡森公式计算。

调频信号的功率分配：

$$P_{FM}=\frac{A^2}{2}=P_c$$

3.4 调频信号的产生和解调

3.4.1 调频信号的产生

调频的方法有：直接调频和间接调频。

• 直接调频：就是用调制信号直接控制正弦波振荡器的频率，使其随调制信号作线性变化。

• 间接调频：将调制信号m(t)先积分后调相。从而产生一个窄带调频信号（NBFM），然后n次倍频，提高调频指数m_f,即可实现宽带调频。

3.4.2 调频信号的解调

非相干解调

调频信号的解调是要产生一个输入调频信号的频率呈线性的输出电压。完成这种频率-电压转换关系的器件简称鉴频器。

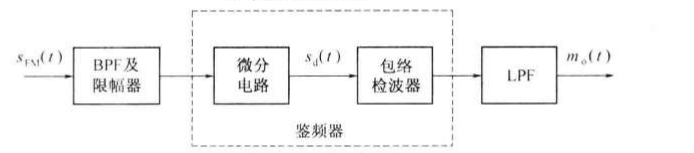
下图是振幅鉴频器原理框图：

鉴频器的特性图：

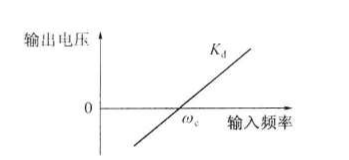
图中，微分器和包络检波器构成了鉴频器，微分器的作用是把幅度恒定的调频波S_FM(t)变成幅度和频率都对消息信号m(t)变化的调幅调频波。

包络检波器的作用是将S_d(t)的幅度变化检出并滤除直流，再经低通滤波器后即可得到解调输出：
$$m_o(t)=K_d{K}_{f}m(t)$$
其中K_d为鉴频器灵敏度。

4 调频系统的抗噪声性能

由上一点可知调频信号的解调有相干解调和非相干解调两种，相干解调仅适用于窄带调频信号，而且需要同步，故应用范围受限；而非相干解调不需要同步信号对于NBFM和WBFM信号均适用，因此非相干解调是FM的主要调制方式。

FM的非相干解调的抗噪声性能分析模型：

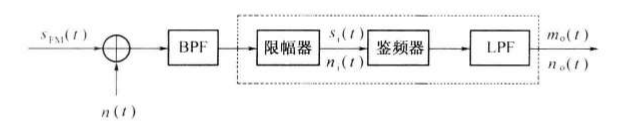
4.1 输入信噪比

$$\frac{S_i}{N_i}=\frac{A^2/2}{n_0{B}_{FM}}=\frac{A^2}{2n_0{B}_{FM}}$$

B_FM为FM信号的带宽，即带通滤波器。

4.2 大信噪比时的解调增益

在解调器输入信噪比足够大时，信号和噪声可以分开来计算。解调器的输出信噪比为：

输出信号的平均功率为：

$$S_0=\overline{m_o^2(t)}=(K_d{K}_f{)}^2\overline{m^2(t)}$$

解调器最终输出的噪声功率为：

$$N_0=\frac{8{\pi }^2{K}_d^2{n}_0{F}_m^3}{3A^2}$$

输出信噪比为：

$$\frac{S_o}{N_o}=\frac{3A^2{K}_f^2\overline{m^2(t)}}{8{\pi }^2{n}_0{f}_m^3}$$
如果调制信号$m(t)=\cos {\omega }_{m}t$(单音调制)，则有

$$\begin{gathered} \frac{S_o}{N_o}=3m_f^2(m_f+1)\frac{S_i}{N_i} \\ {G}_{FM}=3m_f^2(m_f+1) \\ {B}_{FM}=2(m_f+1)f_m=2(\Delta f+f_m) \end{gathered}$$

可见在大信噪比情况下，m_f增大–>B_FM增大–>G_FM增大。这说明，调频系统可以通过增加传输带宽来改善抗噪声性能。

注意，FM系统以带宽换取输出信噪比改善并不是无止境的。带宽增加–>输入噪声功率增大–>输入信噪比下降–>出现门限效应。

4.3 小信噪比时的门限效应

当输入信噪比（S_i/N_i）低于门限值时，鉴频器也会出现门限效应。门限效应是所有非相干解调器都存在的一种特性；而相干解调器不存在门限效应。

当FM调制的输入信噪比低于一定数值是，解调器的输出信噪比急剧恶化，这种现象叫做门限效应。

结论：
（1）门限值与调制指数m_f有关。m_f越大门限值越高。
（2）m_f越大，输出信噪比的改善越明显。
（3）m_f越大，FM信号输出信噪比下降得越快。

4.4 预加重和去加重

预加重：人为提升调制信号的高频分量；
去加重：将调制信号高频端的噪声衰减，同时把调制信号高频分量的幅度恢复到初始值。

4.5 各种模拟调制系统的比较

抗噪声性能：FM最好，DSB/SSB、VSB次之，AM最差；

频谱利用率：SSB最高，VSB较高，DSB/AM次之，FM最差；

功率利用率：FM最高，DSB/SSB、VSB次之，AM最差。

设备复杂度：AM最简单，DSB/FM次之，VSB较复杂，SSB最复杂。

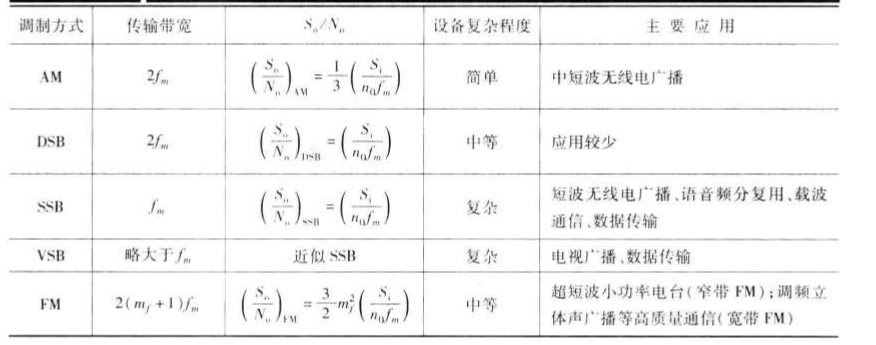
• 比较的条件是：假设所有系统在接收机输入端具有相等的输入信号功率S_i.，且加性噪声都是均值为0、双边功率谱密度为n₀/2的高斯白噪声，基带信号m(t)的带宽均为f_m，并在所有系统中都满足

$$\{\begin{array}{l}\overline{m(t)}=0\\ \overline{m^2(t)}=\frac{1}{2}\\ |m(t){|}_{max}=1\end{array}$$

4.4 预加重和去加重

预加重：人为提升调制信号的高频分量；

去加重：将调制信号高频端的噪声衰减，同时把调制信号高频分量的幅度恢复到初始值。

4.5 各种模拟调制系统的比较

抗噪声性能：FM最好，DSB/SSB、VSB次之，AM最差；

频谱利用率：SSB最高，VSB较高，DSB/AM次之，FM最差；

功率利用率：FM最高，DSB/SSB、VSB次之，AM最差。

设备复杂度：AM最简单，DSB/FM次之，VSB较复杂，SSB最复杂。

• 比较的条件是：假设所有系统在接收机输入端具有相等的输入信号功率S_i.，且加性噪声都是均值为0、双边功率谱密度为n₀/2的高斯白噪声，基带信号m(t)的带宽均为f_m，并在所有系统中都满足

$$\{\begin{array}{l}\overline{m(t)}=0\\ \overline{m^2(t)}=\frac{1}{2}\\ |m(t){|}_{max}=1\end{array}$$

通信原理 曹丽娜 樊昌信 指导书 课后习题答案 百度网盘下载 kitz

通信原理教材 百度网盘下载 srsx

最后

以上就是炙热蓝天最近收集整理的关于通信原理期末复习笔记 -- 第五章 模拟调制系统的全部内容，更多相关通信原理期末复习笔记内容请搜索靠谱客的其他文章。