一、原理

相机标定是我们相机拍摄的物体都处于三维世界坐标系中，而相机拍摄成像时把三维相机坐标系向二维图像坐标系转换。不同镜头成像时的转换矩阵不同可能引入失真，标定的作用是近似地估算出转换矩阵和失真系数。为了估算，需要知道若干点的三维世界坐标系中的坐标和二维图像坐标系中的坐标。传统的照相机标定方法是通过世界坐标集(Xi,Yi,Zi)，以及它们在图像平面上的投影坐标集(ui,vi)，计算相机投影矩阵M中的 11个未知参数，需要严格个出三个两两互相垂直的平面来做标定（条件较为严格，一般情况难以实现）。而棋盘标定只需要两个平面，只需要黑白格子相交的角点来标记会比原始标定容易许多。总而言之棋盘标定的意义就在于克服了传统标定法需要的高精度标定物的缺点，而仅需使用一个打印出来的棋盘格就可以。

二、相机参数

2.1计算单应性矩阵H

根据之前博客介绍的摄像机模型，设三维世界坐标的点为X=[X,Y,Z,1]TX=[X,Y,Z,1]T，二维相机平面像素坐标为m=[u,v,1]Tm=[u,v,1]T，所以标定用的棋盘格平面到图像平面的单应性关系为：
s0m=K[R,T]X
其中s为尺度因子，K为摄像机内参数，R为旋转矩阵，T为平移向量。令

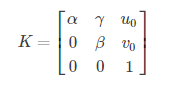
注意，s对于齐次坐标来说，不会改变齐次坐标值。张氏标定法中，将世界坐标系狗仔在棋盘格平面上，令棋盘格平面为Z=0的平面。则可得

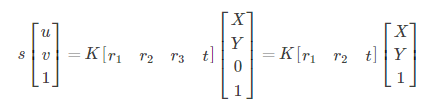
我们把K[r1, r2, t]叫做单应性矩阵H，即

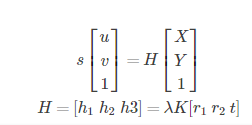
H是一个齐次矩阵，所以有8个未知数，至少需要8个方程，每对对应点能提供两个方程，所以至少需要四个对应点，就可以算出世界平面到图像平面的单应性矩阵H。

2.2计算内参数矩阵

由上式可得

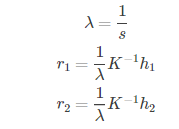
由于旋转矩阵是个酉矩阵，r1和r2正交，可得

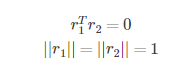
代入可得：

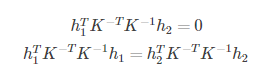
每个单应性矩阵能提供两个方程，而内参数矩阵包含5个参数，要求解，至少需要3个单应性矩阵。为了得到三个不同的单应性矩阵，我们使用至少三幅棋盘格平面的图片进行标定。通过改变相机与标定板之间的相对位置来得到三个不同的图片。为了方便计算，定义如下：

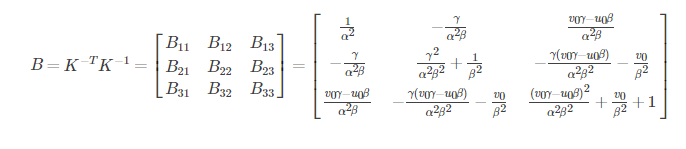
可以看到，B是一个对称阵，所以B的有效元素为六个，让这六个元素写成向量b，即

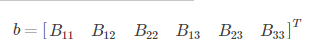
可以推导得到

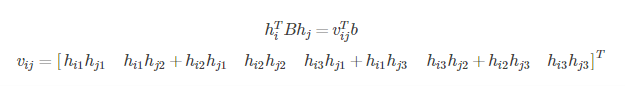
利用约束条件可以得到：

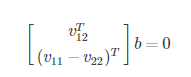
通过上式，我们至少需要三幅包含棋盘格的图像，可以计算得到B，然后通过cholesky分解，得到相机的内参数矩阵K。

2.3计算外参数矩阵

由之前的推导，可得
 

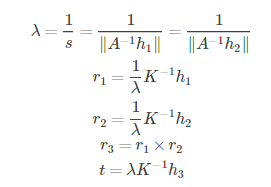
三、代码及实现

3.1代码

# coding=utf-8
import numpy as np
import cv2
import glob
# 终止标准
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
#w = 7
#h = 7
#准备对象点，如（0,0,0），（1,0,0），（2,0,0）......，（6,5,0）
#objp = np.zeros((w*h,3), np.float32)
objp = np.zeros((7*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:7].T.reshape(-1,2)

# 用于存储所有图像中的对象点和图像点的数组。
objpoints = [] # 在现实世界空间的3d点
imgpoints = [] # 图像平面中的2d点。
#glob是个文件名管理工具
images = glob.glob('C:/Users/jxtx/计算机视觉/4/*.jpg')
print('...loading')
for fname in images:
    #对每张图片，识别出角点，记录世界物体坐标和图像坐标
    print('processing img:{fname}')
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)#转灰度
    print('grayed')
    #寻找角点，存入corners，ret是找到角点的flag
    #ret, corners = cv2.findChessboardCorners(gray, (w, h),None)
    ret, corners = cv2.findChessboardCorners(gray, (7, 7),None)

    # 如果找到，添加对象点，图像点（精炼后）
    if ret == True:
        print('chessboard detected')
        objpoints.append(objp)
        #执行亚像素级角点检测
        corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
        imgpoints.append(corners2)

        # 绘制并显示角点
        #img = cv2.drawChessboardCorners(img, (w,h), corners2,ret)
        img = cv2.drawChessboardCorners(img, (7,7), corners2,ret)
        cv2.namedWindow('img',0)
        cv2.resizeWindow('img', 500, 500)
        cv2.imshow('img',img)
        cv2.waitKey(500)
        cv2.destroyAllWindows()
'''
传入所有图片各自角点的三维、二维坐标，相机标定。
每张图片都有自己的旋转和平移矩阵，但是相机内参和畸变系数只有一组。
mtx，相机内参；dist，畸变系数；revcs，旋转矩阵；tvecs，平移矩阵。
'''

img2 = cv2.imread("C:/Users/13799/PycharmProjects/untitled1/test/1.jpg")
print("type objpoints:{objpoints[0].shape}")
print("type imgpoints:{imgpoints[0].shape}")

ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1],None,None)
h,  w = img2.shape[:2]


'''
优化相机内参（camera matrix），这一步可选。
参数1表示保留所有像素点，同时可能引入黑色像素，
设为0表示尽可能裁剪不想要的像素，这是个scale，0-1都可以取。
'''
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))
#纠正畸变
dst = cv2.undistort(img2, mtx, dist, None, newcameramtx)

# 裁剪图像，输出纠正畸变以后的图片
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('calibresult.png',dst)

#打印我们要求的两个矩阵参数
print ("newcameramtx外参:n",newcameramtx)
print ("dist畸变值:n",dist)
print ("newcameramtx旋转（向量）外参:n",rvecs)
print ("dist平移（向量）外参:n",tvecs)
#计算误差
tot_error = 0
for i in range(len(objpoints)):
    imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
    tot_error += error

print ("total error: ", tot_error/len(objpoints))

3.2图片集

3.3结果展示

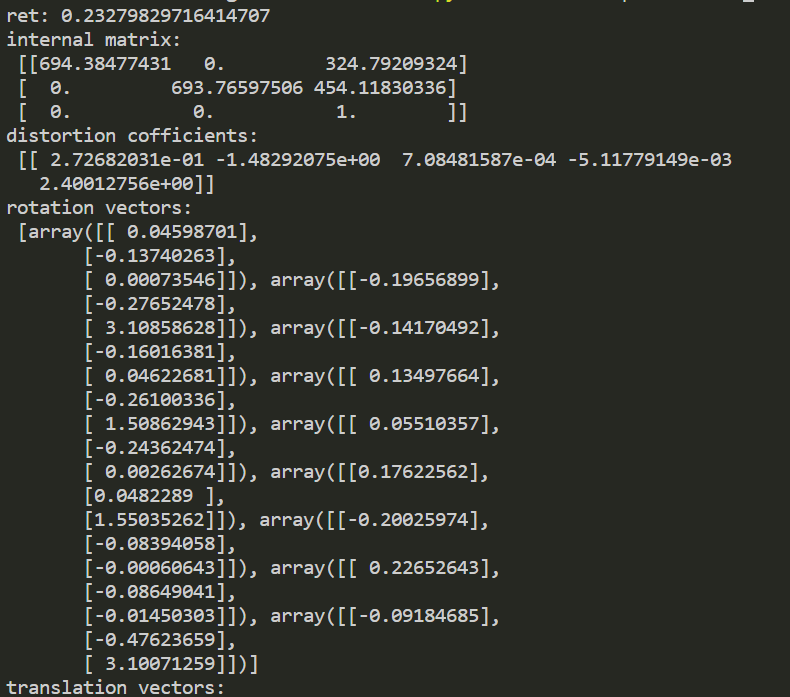
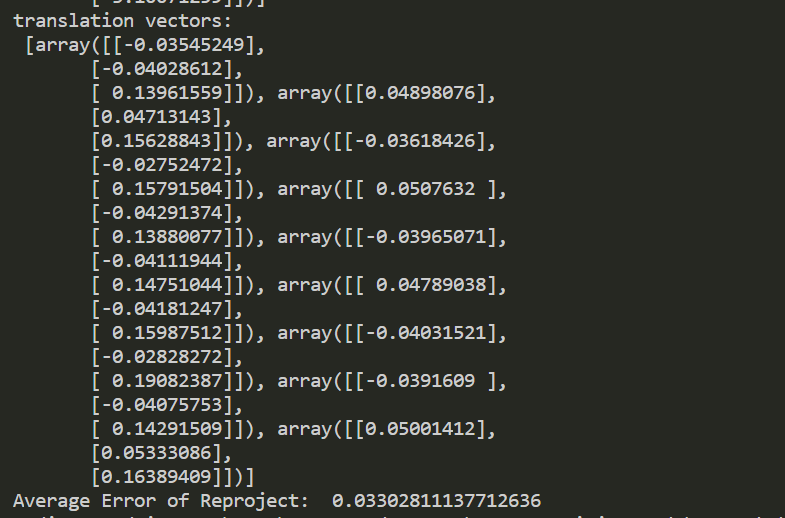
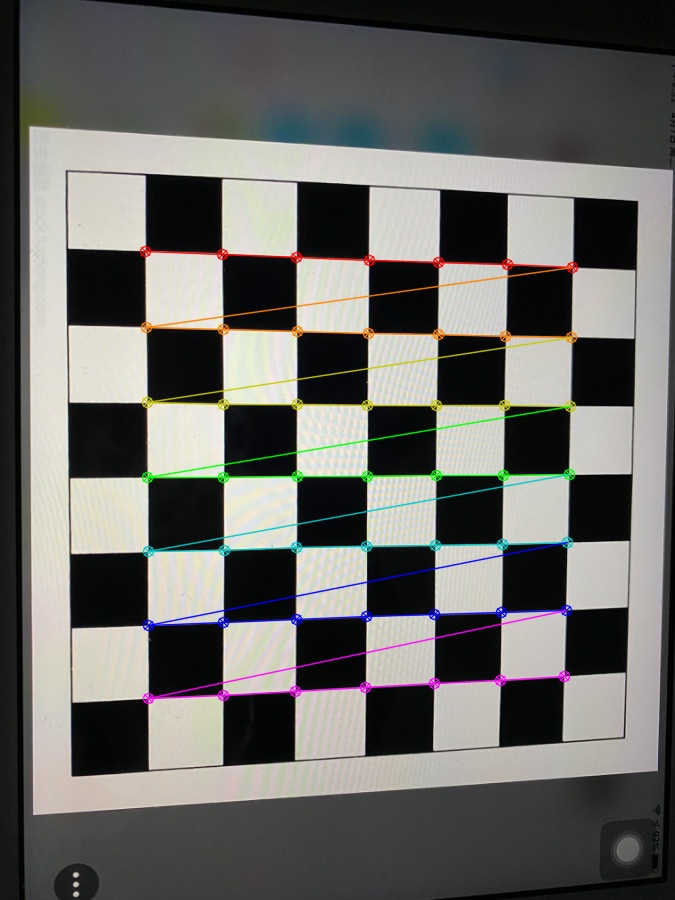
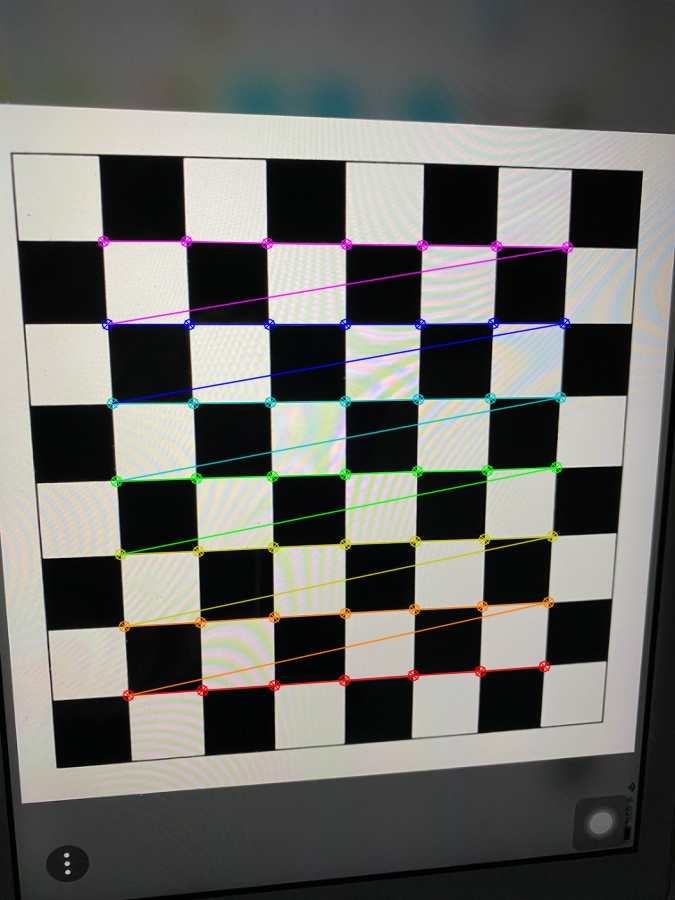
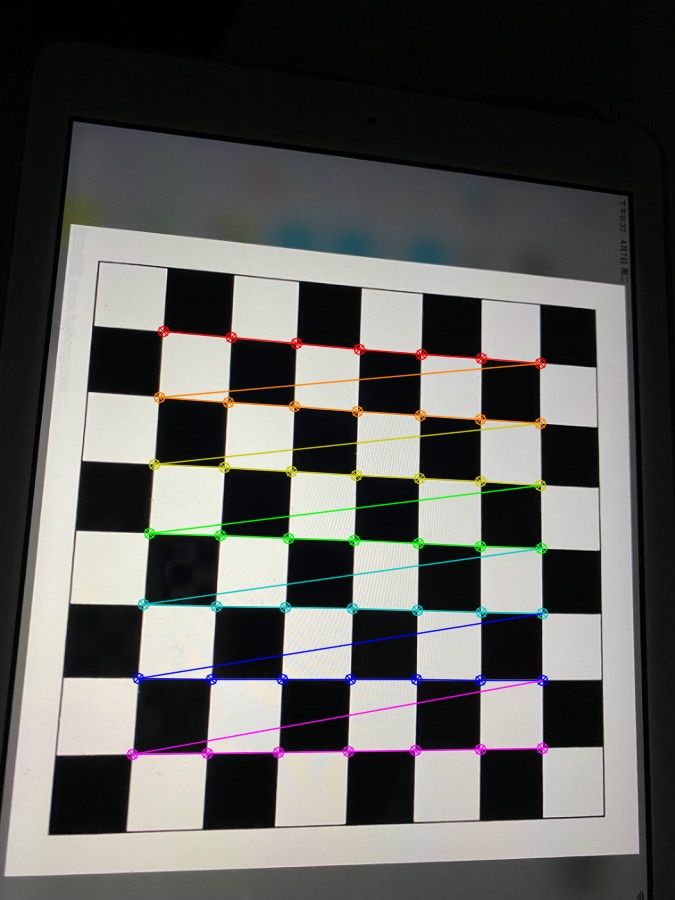
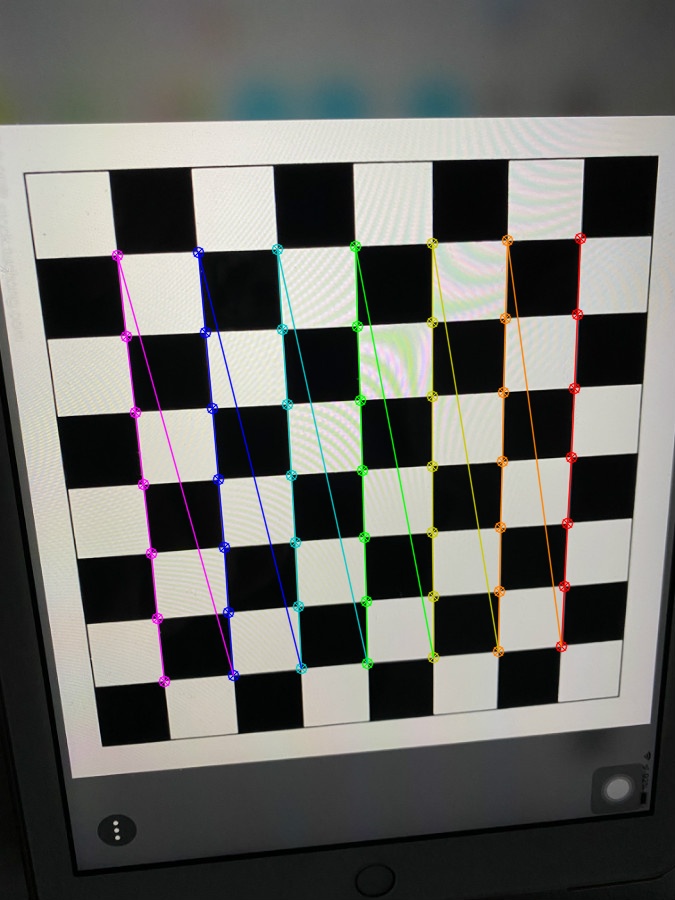
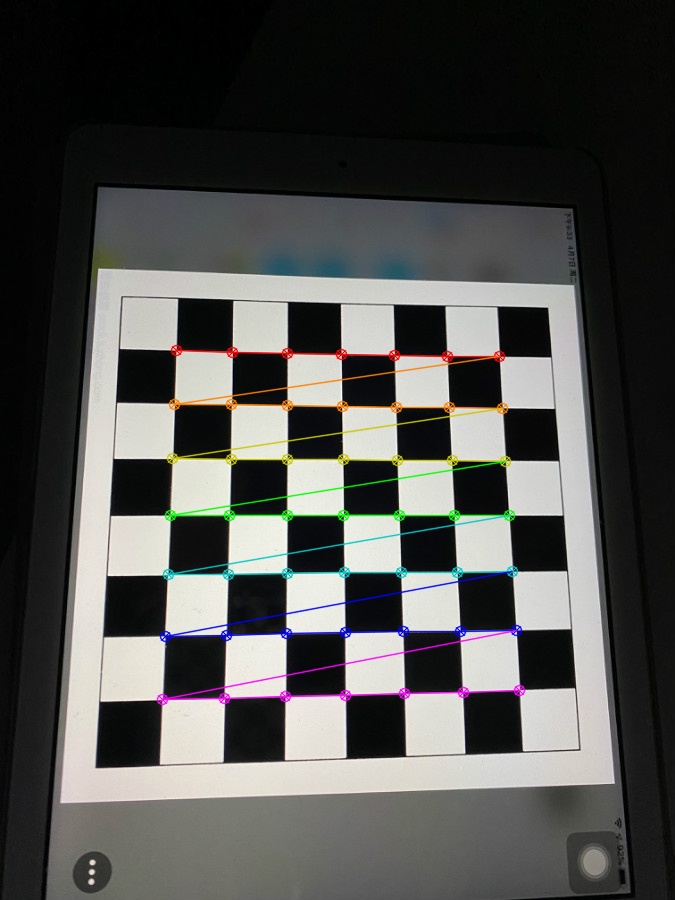
四、出现的错误及解决

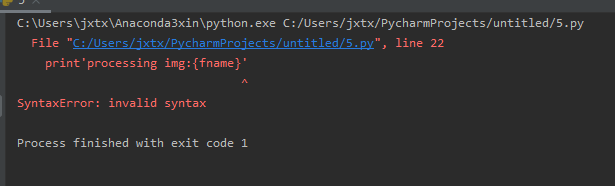
将 print’processing img:{fname}'改成print(‘processing img:{fname}’)

最后

以上就是直率饼干为你收集整理的棋盘格标定一、原理二、相机参数三、代码及实现四、出现的错误及解决的全部内容，希望文章能够帮你解决棋盘格标定一、原理二、相机参数三、代码及实现四、出现的错误及解决所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。