相机标定（棋盘格标定法）

相机标定（棋盘格标定法）

1、相机标定

1.1、相机标定简介

在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数的过程就称之为相机标定（或摄像机标定）

1.2、相机标定意义

计算机视觉的基本任务之一是从摄像机获取的图像信息出发计算三维空间中物体的几何信息，并由此重建和识别物体，而空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系是由摄像机成像的几何模型决定的，这些几何模型参数就是摄像机参数。在大多数条件下，这些参数必须通过实验与计算才能得到。无论是在图像测量或者机器视觉应用中，相机参数的标定都是非常关键的环节，其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此，做好相机标定是做好后续工作的前提，提高标定精度是科研工作的重点所在。

1.3、相机标定作用

1、相机在出厂之前都需要进行相机标定，用软件的方法校正生成的图像，避免拍摄出的图像产生桶形和枕形畸变

2、根据相机成像的几何模型，将世界坐标系中的3D物体映射到2D成像平面上
3、求解多个相机对之间的映射关系。

2、相机参数

2.1、相机参数的同步策略

同步标定内部参数和外部参数，一般包括两种策略

1. 光学标定: 利用已知的几何信息(如定长棋盘格)实现参数求解
2. 自标定: 在静态场景中利用 structure from motion估算参数。

2.2、内参数

相机的内参数是六个分别为：1/dx、1/dy、r、u0、v0、f。

dx和dy表示：x方向和y方向的一个像素分别占多少长度单位，即一个像素代表的实际物理值的大小，其是实现图像物理坐标系与像素坐标系转换的关键。u0，v0表示图像的中心像素坐标和图像原点像素坐标之间相差的横向和纵向像素数。

2.3、外参数

相机的外参数是6个：三个轴的旋转参数分别为（ω、δ、 θ）,然后把每个轴的33旋转矩阵进行组合（即先矩阵之间相乘），得到集合三个轴旋转信息的R，其大小还是33；T的三个轴的平移参数（Tx、Ty、Tz）。R、T组合成成的3*4的矩阵，其是转换到标定纸坐标的关键。其中绕X轴旋转θ，则其如图：

2.4、畸变参数

畸变参数是：k1,k2,k3径向畸变系数，p1,p2是切向畸变系数。径向畸变发生在相机坐标系转图像物理坐标系的过程中。而切向畸变是发生在相机制作过程，其是由于感光元平面跟透镜不平行。其如下：

2.4.1、径向畸变

产生原因是光线在远离透镜中心的地方比靠近中心的地方更加弯曲径向畸变主要包含桶形畸变和枕形畸变两种。下面两幅图是这两种畸变的示意：

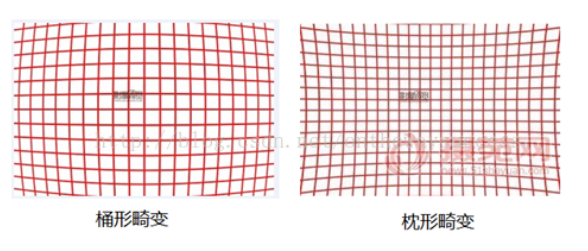
2.4.2、切向畸变

产生的原因透镜不完全平行于图像平面，这种现象发生于成像仪被粘贴在摄像机的时候。

3、实验内容

3.1、实验要求

1.制作棋盘格（每个格子的大小可测量），最好是打印出来，贴在平面上
2.根据棋盘格，采集10-20张图片，提取角点
3.解算出内外参数，外部参数最好能可视化

3.2、制作棋盘格并采集图片

因为没有打印条件，所以在电脑上绘制了一个9x7的棋盘格，并采集16张图片作为数据集，图片如下：

3.3、实验过程

1、在matlab应用中找到Camera Calibrator

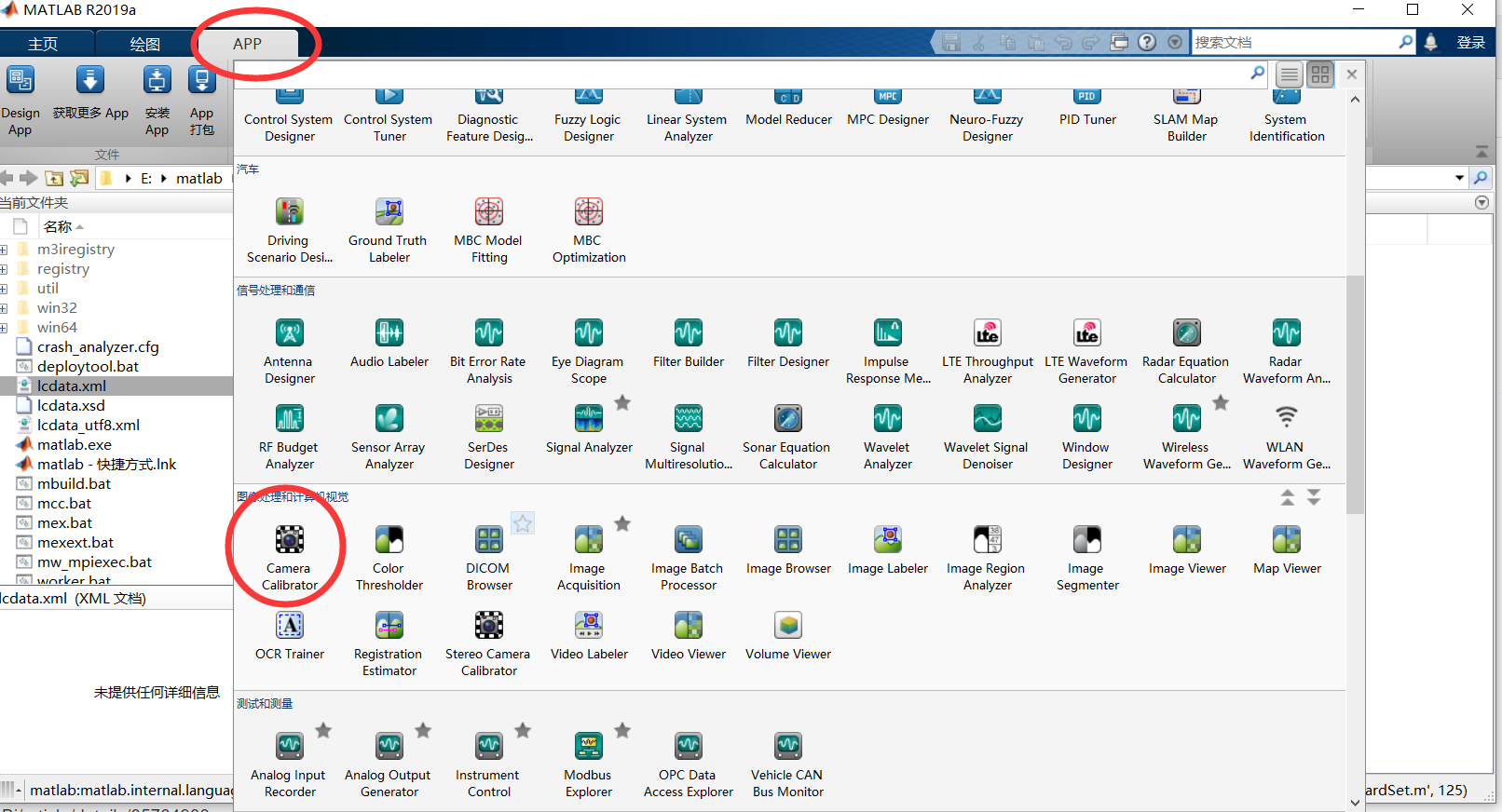
2、将采集的图片读入

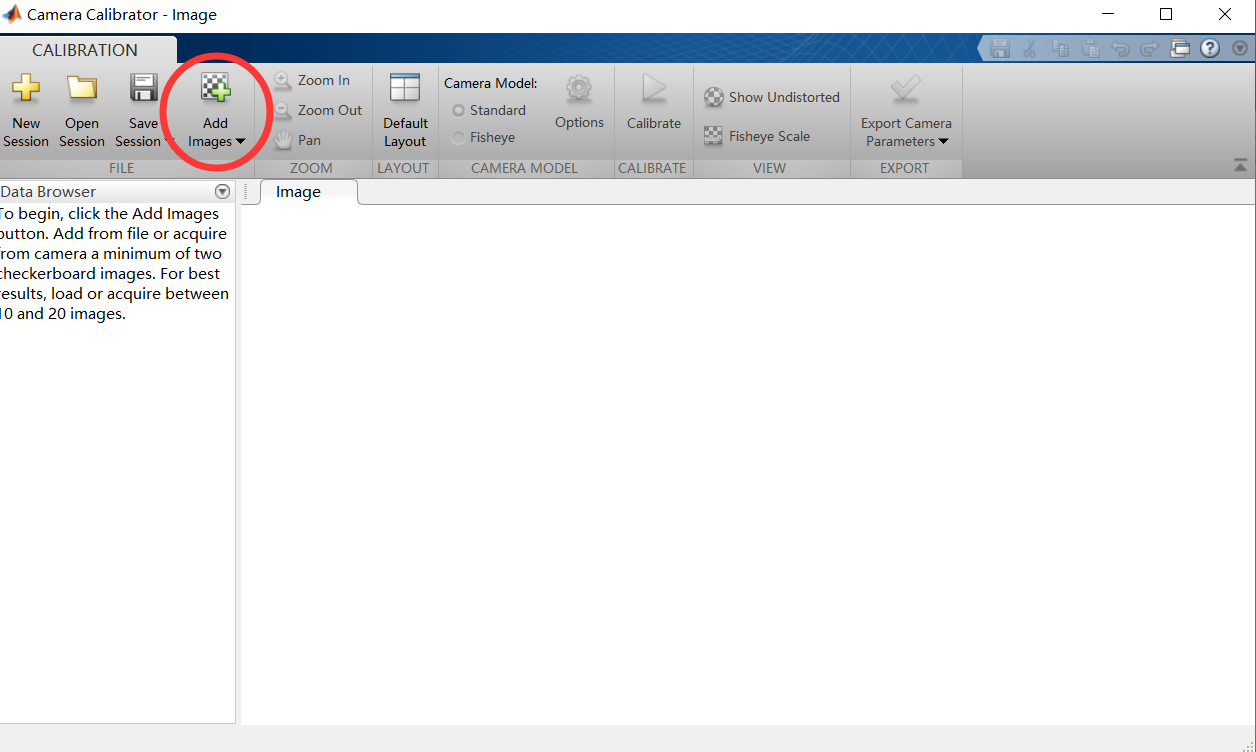
3、输入棋盘格的大小

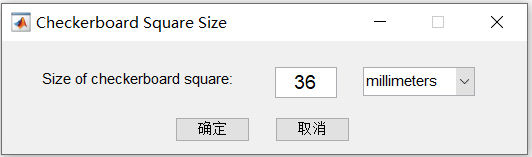
*注意单位转换

4、读入结果

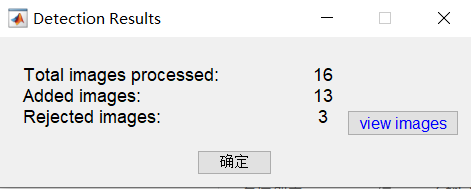
图片加载完毕后会弹出提示框，可以看到读入的16张图片里有3张是被拒绝的（不合格的）

5、角点检测结果

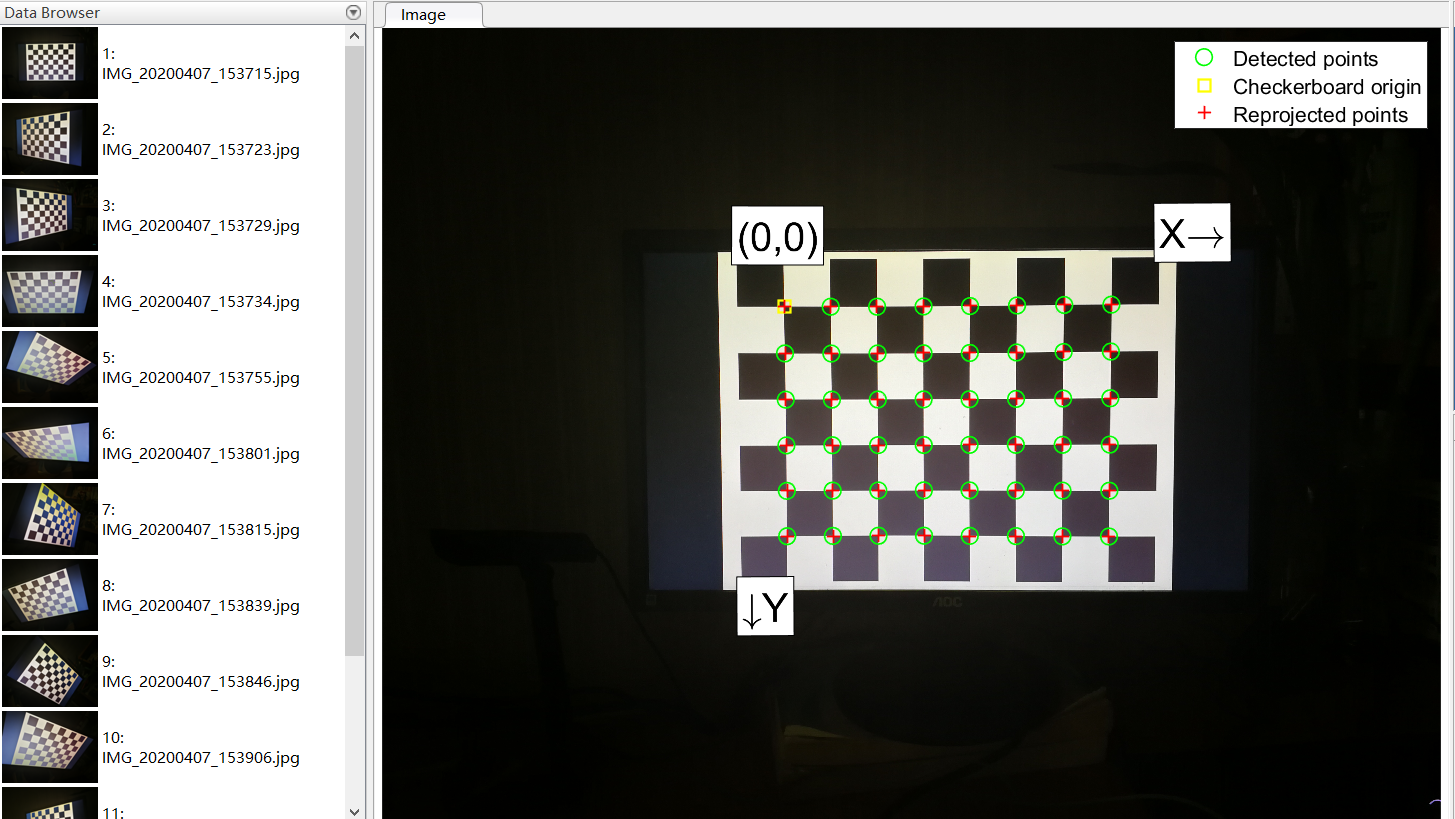
绿色圈圈出的为检测点
红色十字标记的为投影点
6、求解出的参数
将参数输出

找到对应的参数，如内参矩阵IntrinsicMatrix

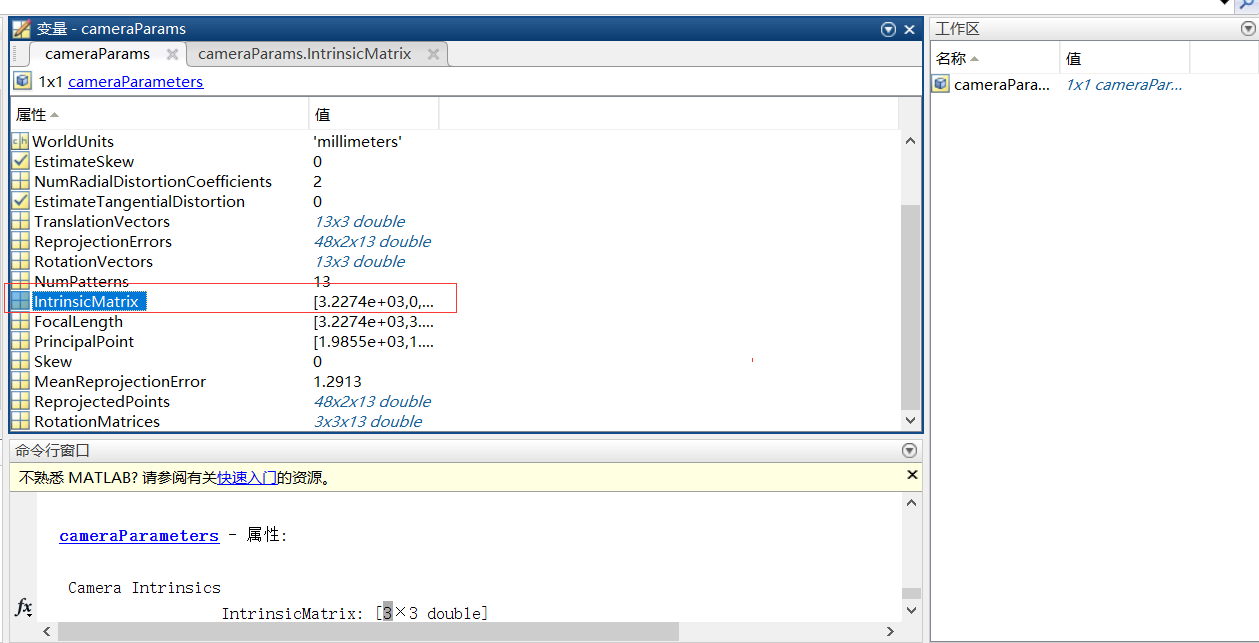
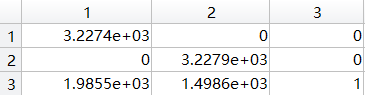
内参数矩阵IntrinsicMatrix

径向畸变RadialDistortion

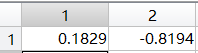
切向畸变TangentialDistortion

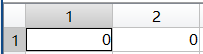
旋转矩阵RotationMatrices

val(:,:,1) =

0.9994   -0.0104   -0.0320
0.0119    0.9988    0.0484
0.0315   -0.0487    0.9983

val(:,:,2) =

0.8595    0.0265   -0.5105
0.0032    0.9984    0.0571
0.5111   -0.0507    0.8580

val(:,:,3) =

0.8160   -0.0555    0.5754
0.0303    0.9981    0.0533

-0.5772 -0.0260 0.8162

val(:,:,4) =

0.9995   -0.0082   -0.0300
0.0215    0.8799    0.4746
0.0225   -0.4750    0.8797

val(:,:,5) =

0.8373    0.3010    0.4564

-0.5366 0.6126 0.5803
-0.1049 -0.7308 0.6745

val(:,:,6) =

0.9074   -0.0197   -0.4198
0.3312    0.6486    0.6853
0.2588   -0.7609    0.5950

val(:,:,7) =

0.6924    0.3109    0.6511

-0.2539 0.9497 -0.1834
-0.6753 -0.0384 0.7365

val(:,:,8) =

0.9248   -0.2562   -0.2813
0.3535    0.8522    0.3858
0.1408   -0.4562    0.8786

val(:,:,9) =

0.7095    0.5490    0.4418

-0.5756 0.8132 -0.0862
-0.4066 -0.1932 0.8930

val(:,:,10) =

0.8581    0.1882    0.4778

-0.4134 0.8051 0.4254
-0.3046 -0.5625 0.7686

val(:,:,11) =

0.7846   -0.0860   -0.6140
0.0741    0.9962   -0.0449
0.6155   -0.0103    0.7880

val(:,:,12) =

0.9996    0.0280    0.0088

-0.0289 0.8881 0.4587
0.0051 -0.4588 0.8885

val(:,:,13) =

0.9997   -0.0025   -0.0259
0.0044    0.9975    0.0703
0.0257   -0.0703    0.9972

平移向量TranslationVectors

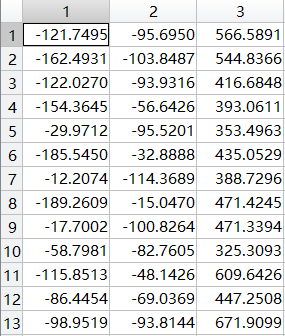
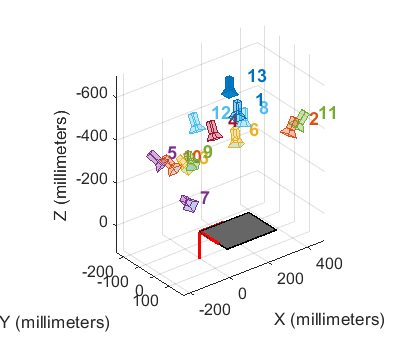
外参数

以相机为中心

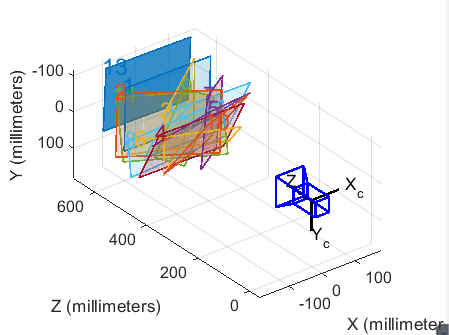
以棋盘格为中心

参考资料

https://blog.csdn.net/KillMeHealMe/article/details/81192685
https://blog.csdn.net/JennyBi/article/details/85764988

最后

以上就是洁净台灯为你收集整理的相机标定（棋盘格标定法）的全部内容，希望文章能够帮你解决相机标定（棋盘格标定法）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。