1：相机标定

1.1原理介绍

相机标定指建立相机图像像素位置与场景点位置之间的关系，根据相机成像模型，由特征点在图像中坐标与世界坐标的对应关系，求解相机模型的参数。相机需要标定的模型参数包括内部参数和外部参数。

针孔相机成像原理其实就是利用投影将真实的三维世界坐标转换到二维的相机坐标上去，其模型示意图如下图所示：

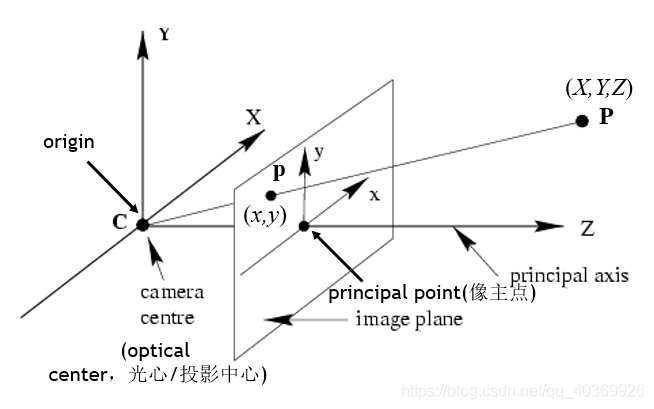
一般来说，标定的过程分为两个部分：
第一步是从世界坐标系转为相机坐标系，这一步是三维点到三维点的转换，包括R，t（相机外参，确定了相机在某个三维空间中的位置和朝向）等参数；
第二部是从相机坐标系转为成像平面坐标系（像素坐标系），这一步是三维点到二维点的转换，包括K（相机内参，是对相机物理特性的近似）等参数；
投影矩阵 ： P=K [ R | t ] 是一个3×4矩阵，混合了内参和外参而成。

1.2相机标定的意义

（1）一个是由于每个镜头的在生产和组装过程中的畸变程度各不相同，通过相机标定可以校正这种镜头畸变，生成矫正后的图像——矫正透镜畸变；
（2）另一个是根据标定后的到的相机参数建立相机成像几何模型，由获得的图像重构出三维场景。具体来说：当我们用摄像机拍照时，从照片里得到一些空间信息（比如距离，尺寸等），是要利用二维图像得到三维信息。我们拍照的时候把空间物体信息通过摄像机变成了二维图像，这个过程本来是不可逆的。但如果我们可以找到一个摄像机的数学模型，就可以 ：从二维图像+模型逆推得到原来三维信息。标定就是在找这个模型。

1.3相机标定的作用：
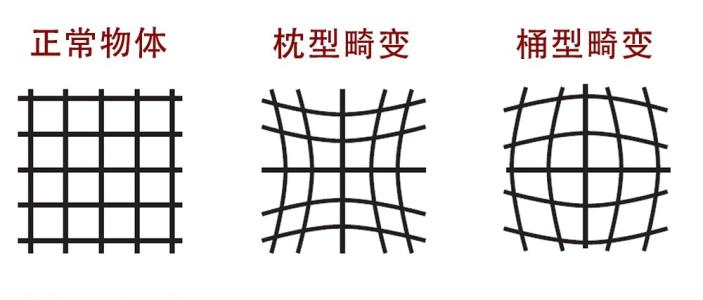
1）相机在出厂之前都需要进行相机标定，用软件的方法校正生成的图像，避免拍摄出的图像产生桶形和枕形畸变；

（2）根据相机成像的几何模型，将世界坐标系中的3D物体映射到2D成像平面上；
（3）求解多个相机对之间的映射关系。

2：相机标定步骤

1、打印一张模板并贴在一个平面上；
2、从不同角度拍摄若干张模板图像；
3、检测出图像中的特征点；
4、求出摄像机的外参数（单应性矩阵）和内参数（最大似然估计）
5、求出畸变系数；
6、优化求精。

3：进行实验

实验素材：

代码：

import cv2
import numpy as np
import glob

# 找棋盘格角点
# 阈值
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
#棋盘格模板规格
w = 9   #内角点个数，内角点是和其他格子连着的点
h = 6

# 世界坐标系中的棋盘格点,例如(0,0,0), (1,0,0), (2,0,0) ....,(8,5,0)，去掉Z坐标，记为二维矩阵
objp = np.zeros((w*h,3), np.float32)
objp[:,:2] = np.mgrid[0:w,0:h].T.reshape(-1,2)
# 储存棋盘格角点的世界坐标和图像坐标对
objpoints = [] # 在世界坐标系中的三维点
imgpoints = [] # 在图像平面的二维点

images = glob.glob('C:/Users/samz305s/Desktop/sy/*.jpg')
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
    # 找到棋盘格角点
    # 棋盘图像(8位灰度或彩色图像)  棋盘尺寸  存放角点的位置
    ret, corners = cv2.findChessboardCorners(gray, (w,h),None)
    # 如果找到足够点对，将其存储起来
    if ret == True:
        # 角点精确检测
        # 输入图像 角点初始坐标 搜索窗口为2*winsize+1 死区 求角点的迭代终止条件
        cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
        objpoints.append(objp)
        imgpoints.append(corners)
        # 将角点在图像上显示
        cv2.drawChessboardCorners(img, (w,h), corners, ret)
        cv2.imshow('findCorners',img)
        cv2.waitKey(1000)
cv2.destroyAllWindows()
#标定、去畸变
# 输入：世界坐标系里的位置 像素坐标 图像的像素尺寸大小 3*3矩阵，相机内参数矩阵 畸变矩阵
# 输出：标定结果 相机的内参数矩阵 畸变系数 旋转矩阵 平移向量
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
# mtx：内参数矩阵
# dist：畸变系数
# rvecs：旋转向量 （外参数）
# tvecs ：平移向量 （外参数）
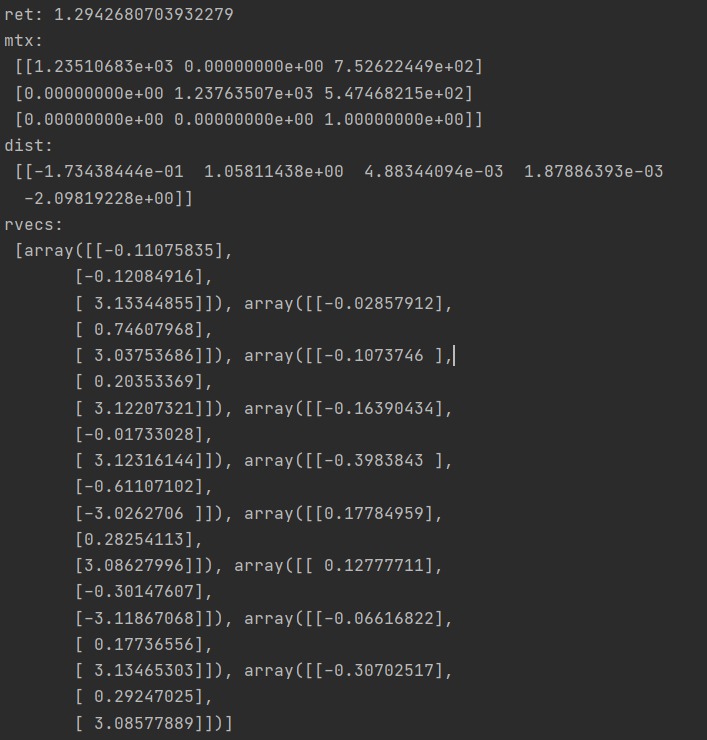
print (("ret:"),ret)
print (("mtx:n"),mtx)        # 内参数矩阵
print (("dist:n"),dist)      # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print (("rvecs:n"),rvecs)    # 旋转向量  # 外参数
print (("tvecs:n"),tvecs)    # 平移向量  # 外参数
# 去畸变
img2 = cv2.imread('C:/Users/samz305s/Desktop/sy/5.jpg')
h,w = img2.shape[:2]
# 我们已经得到了相机内参和畸变系数，在将图像去畸变之前，
# 我们还可以使用cv.getOptimalNewCameraMatrix()优化内参数和畸变系数，
# 通过设定自由自由比例因子alpha。当alpha设为0的时候，
# 将会返回一个剪裁过的将去畸变后不想要的像素去掉的内参数和畸变系数；
# 当alpha设为1的时候，将会返回一个包含额外黑色像素点的内参数和畸变系数，并返回一个ROI用于将其剪裁掉
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),0,(w,h)) # 自由比例参数

dst = cv2.undistort(img2, mtx, dist, None, newcameramtx)
# 根据前面ROI区域裁剪图片
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('calibresult.jpg',dst)

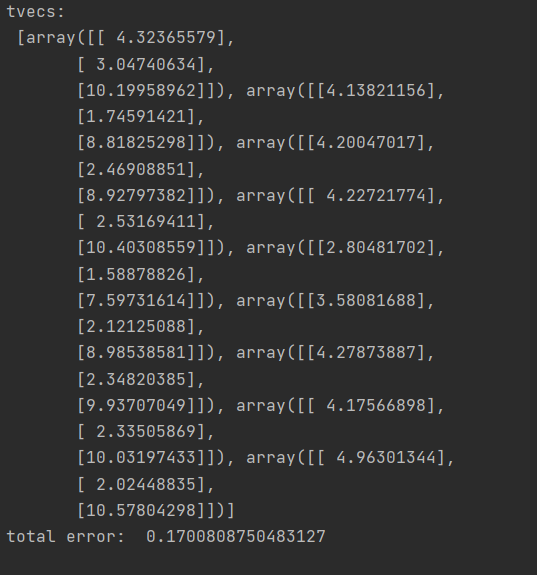
# 反投影误差
# 通过反投影误差，我们可以来评估结果的好坏。越接近0，说明结果越理想。
# 通过之前计算的内参数矩阵、畸变系数、旋转矩阵和平移向量，使用cv2.projectPoints()计算三维点到二维图像的投影，
# 然后计算反投影得到的点与图像上检测到的点的误差，最后计算一个对于所有标定图像的平均误差，这个值就是反投影误差。
total_error = 0
for i in range(len(objpoints)):
    imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
    total_error += error
print (("total error: "), total_error/len(objpoints))

实验结果：

修正后的图片

修正前的图片

4：总结与问题：

1出现的错误：

Traceback (most recent call last):
  File "C:/Users/samz305s/PycharmProjects/jsjsj-sy5/sy.py", line 45, in <module>
    ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)
cv2.error: OpenCV(4.5.2) C:UsersrunneradminAppDataLocalTemppip-req-build-vi271kacopencvmodulescalib3dsrccalibration.cpp:3694: error: (-215:Assertion failed) nimages > 0 in function 'cv::calibrateCameraRO'

Process finished with exit code 1

该错误主要由(-215:Assertion failed) nimages > 0 in function 来说明
原因：
程序没有检测到包含棋盘格的图片或者图片模糊等问题，导致查找棋盘格角点失败
解决办法：
重新拍图片，保持图片的清晰程度以及平整度

最后

以上就是勤奋唇膏为你收集整理的计算机视觉-棋盘格标定1：相机标定2：相机标定步骤3：进行实验4：总结与问题：的全部内容，希望文章能够帮你解决计算机视觉-棋盘格标定1：相机标定2：相机标定步骤3：进行实验4：总结与问题：所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。