资源下载地址:https://download.csdn.net/download/sheziqiong/85734538
资源下载地址:https://download.csdn.net/download/sheziqiong/85734538
1. 实验名称
斐波那契(Fibonacci)数列计算器设计。
2. 实验目的
要求使用合适的逻辑电路的设计方法,通过工具软件 logisim 进行斐波那契(Fibonacci)数列计算器设计和验证,记录实验结果,验证设计是否达到要求。
通过斐波那契(Fibonacci)数列计算器的设计、仿真、验证 3 个训练过程,掌握数字逻辑电路的设计、仿真、调试的方法。
3. 实验所用设备
Logisim2.7.1 软件一套。
4. 实验内容
斐波那契(Fibonacci)数列中每项数值都是其两个直接前项的和,其生成规则如下公式所示:
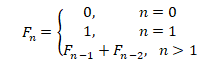
-
求 Fibonacci 数的矩阵算法
求 n 次幂。采用矩阵的快速幂算法,操作次数可优化为 O(log2 n)。
由于 F(47)=(2971215073)10<232,F(48)=(4807526976)10>232,电路中采用 32 位二进制数表示一个整数。为了避免整数溢出,取 2≤n≤47,n 用 6 位二进制数表示。
-
算法描述
Fibonacci() {
初始化:X=matrix A, Start=0;
For (i=5 downto 0)
{
if (Start==0) then
{
if (n[i]==1) then Start=1;
}
Else
{
if (n[i]==1)
then X=X^2A;
else
X=X^2;
}
}
return(X);
}
- 例如:n = (101100)2 = (44)10
- step1:i=5,Start=0,n[5]=1,此时 Start 置 1;
- step2:i=4,Start=1,n[4]=0,此时 X = X2 = A2;
- step3:i=3,Start=1,n[3]=1,此时 X = X2 A = (A2)2A;
- step4:i=2,Start=1,n[2]=1,此时 X = X2 A = ((A2)2A)2 A;
- step5:i=1,Start=1,n[1]=0,此时 X = X2 = (((A2)2A)2 A)2;
- step6:i=0,Start=1,n[0]=0,此时 X = X2 = ((((A2)2A)2 A)2)2;
- 循环执行完后,X = ((((A2)2A)2 A)2)2 = A44
- 矩阵计算模块
(1)计算 X2 模块 sqrX
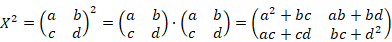
其相应的输入/输出如图 4-1 所示。
这里,a, b, c, d, a′, b′, c′, d′都为 32 位无符号二进制整数。
(2)计算 X2·A 模块 sqrX*A
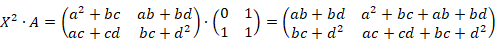
其相应的输入/输出如图 4-2 所示。
这里,a, b, c, d, a″, b″, c″, d″都为 32 位无符号二进制整数。
- 矩阵快速幂算法迭代模块
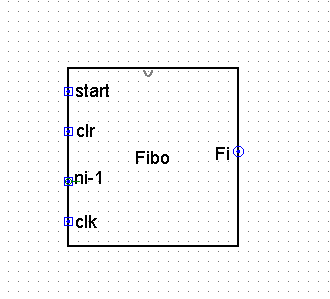
该模块 Fibo 输入/输出端如图 4-3 所示。
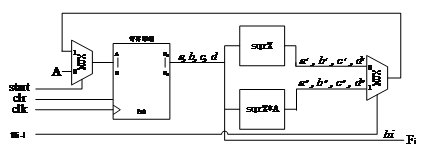
这里,start 为 Fibonacci()算法中的 6 位二进制数 n 左移出的第一个(最高位的)1 的标志信号;ni-1 是 start=1 之后左移出的下一位;clr 为初始化(清零)信号,此时 X = A;clk 为时钟脉冲信号。Fi 为 Fibonacci()算法迭代的中间结果,根据 ni-1 取 0 或 1 来决定 Fi 是取 sqrX 或者 sqrX*A 运算后的矩阵元素 bi,在第 6 个时钟脉冲时,Fi 即为输入 n 的 Fibonacci 数 Fn。
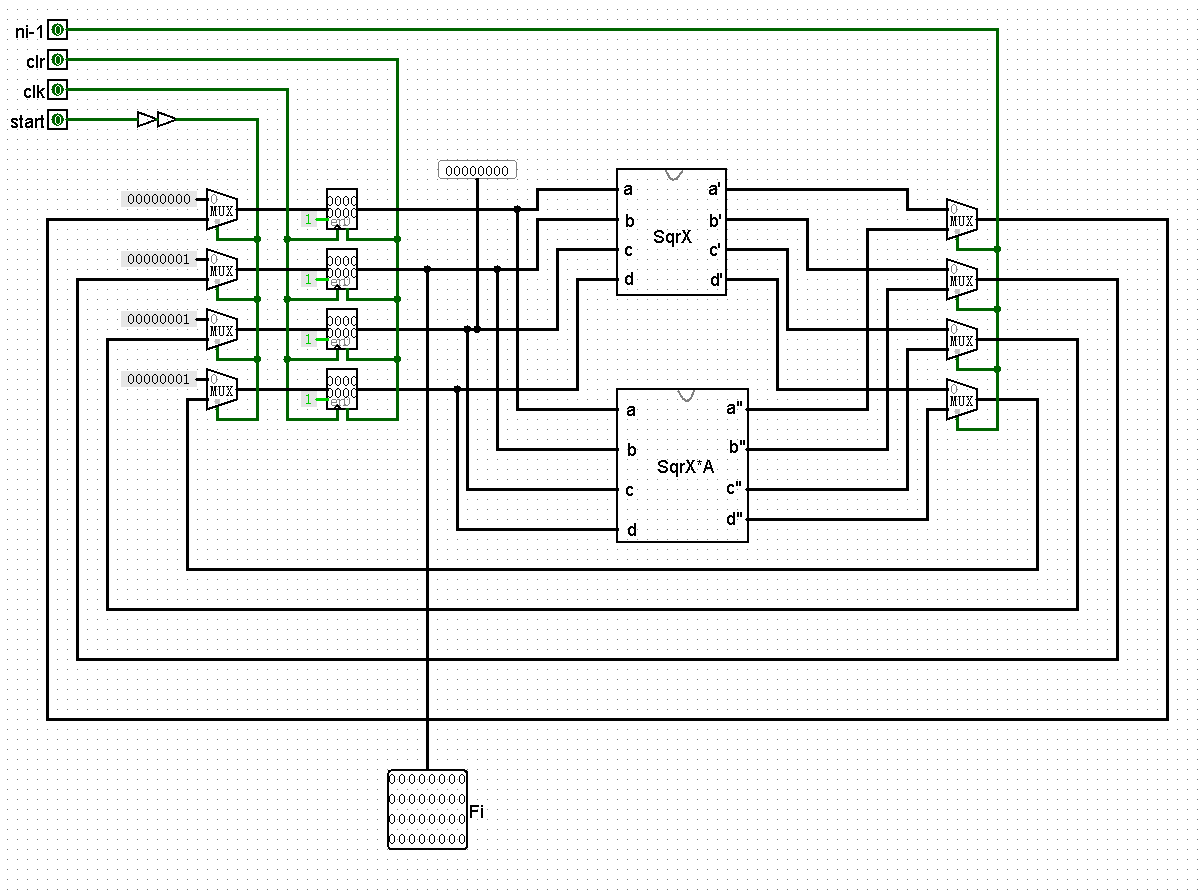
其内部逻辑结构图如图 4-4 所示。
- Fibonacci 数显示模块
将二进制数转换成十进制数在数码显示管上显示出来。
输入为 32 位二进制的 Fibonacci 数 F(n)。
由于 32 位二进制 Fibonacci 数表示的最大十进制数的位数是 10 位,该模块的输出为 10 组 8421BCD 码 D9、D8、D7、D6、D5、D4、D3、D2、D1、D0,每组8421 BCD 码表示 1 位 10 进制数。
- 主模块 main
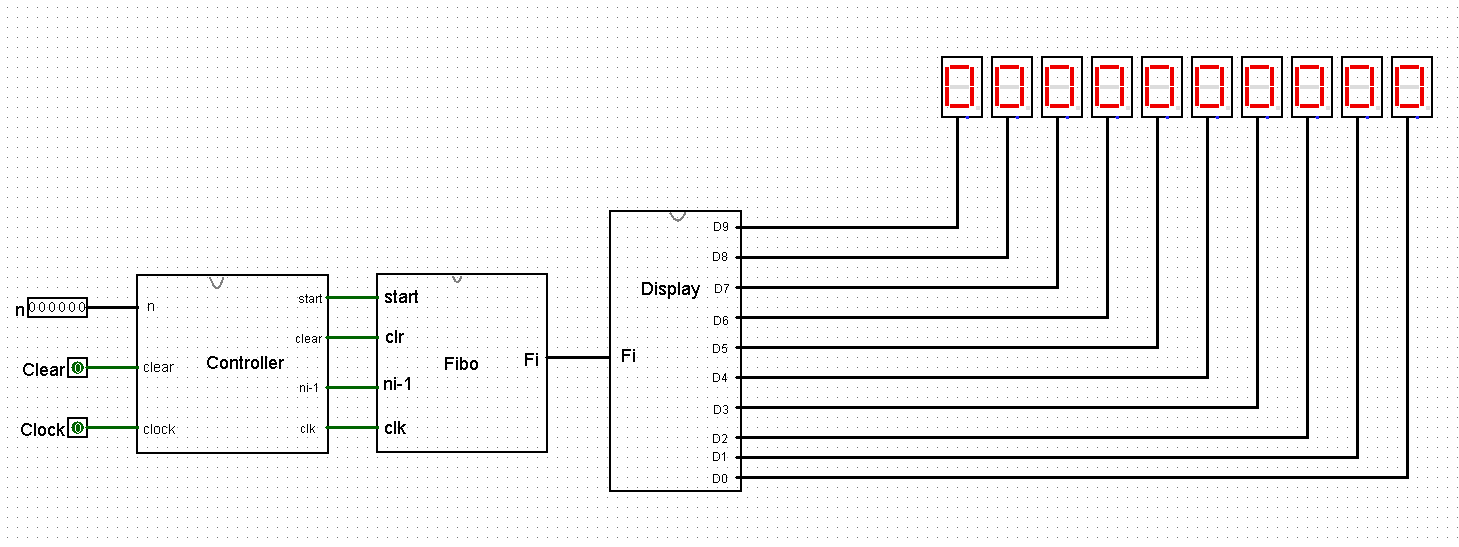
主模块 main 的逻辑结构图 4-5 所示。
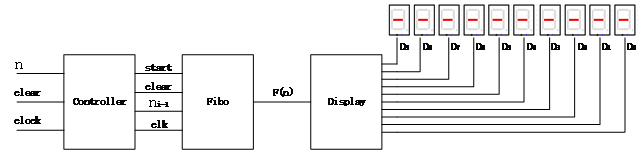
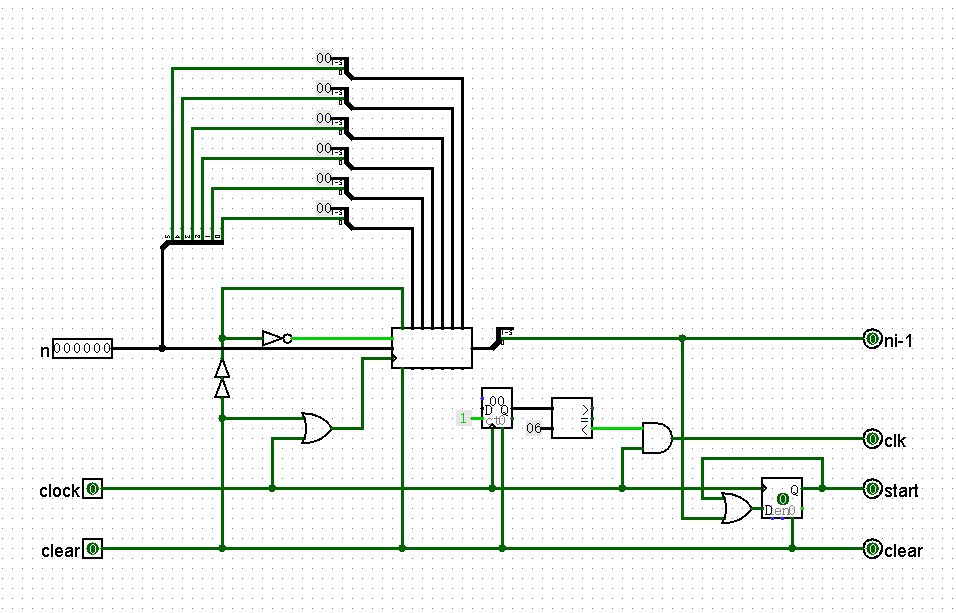
控制器 Controller 中包括三个功能块:6 位二进制数 n 的左移控制电路、6 个时钟脉冲控制电路、start 信号产生电路。
6 位二进制数 n 的左移控制电路,使用一个移位寄存器,在时钟脉冲作用下产生 ni-1。用 clear 信号装入 n,进行移位寄存器的初始化。
使用 1 个 8 位计数器、1 个比较器和适当的门电路,可以控制 Fibo 只接收 6 个 clock 时钟脉冲(产生 clk)。直至下一个 clear 信号初始化后,才准备产生下一组 6 个时钟脉冲。
使用 1 个 D 触发器加适当的门电路构成一个锁存器 Latch,在接收到 n 的最高位 1 时 start=1,直至下一个 clear 信号使 start=0。
在 6 个 clock 时钟脉冲信号后,电路就产生了第 n 个 Fibonacci 数 F(n),并经过 Display 电路转换成十进制数在数码管上显示出来。
5. 实验方案设计
-
斐波那契(Fibonacci)数列计算
要求:
- 给出 Fibonacci 数列通项公式;
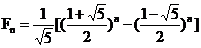
-
给出 Fibonacci 数列的递归算法(指数时间复杂度)形式化描述;
利用递归思想,每次计算当前的值时候,就要引用之前的两个值,一步一步的递归,一直到最起始处,才能用到 F(1)和 F(2)。递归算法时间复杂度为:O(2(N/2))<=T(N)<=O(2N)。
-
给出 Fibonacci 数列的多项式时间复杂度算法形式化描述。
Fibonacci(n)
a=0;
b=1;
if(n==0) return a;
for(i=0; i<n; i++)
{
a=b;
b=a+b;
}
return b;
-
计算矩阵 X2 模块
要求:
-
给出矩阵 X2 计算模块的设计思路;
输入为 a,b,c,d 输出为 a’,b’,c’,d’。其中
a′ = a2+bc
b′ = ab+bd
c′ = ac+cd
d′ = bc+d2
根据输出与输入的关系,用乘法器和加法器连接即可。
-
给出 logisim 软件绘制的电路图(经过仿真验证基本正确);
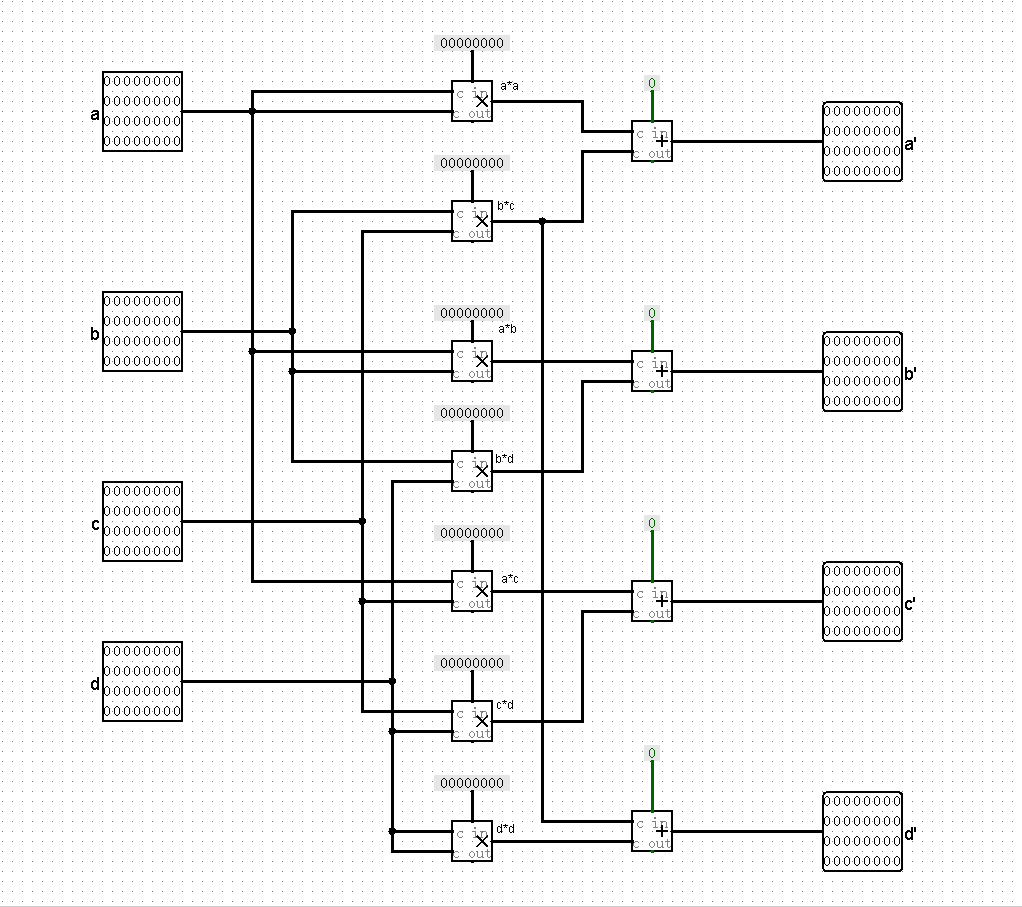
- 对矩阵 X2 模块进行封装,给出封装后的模块图。
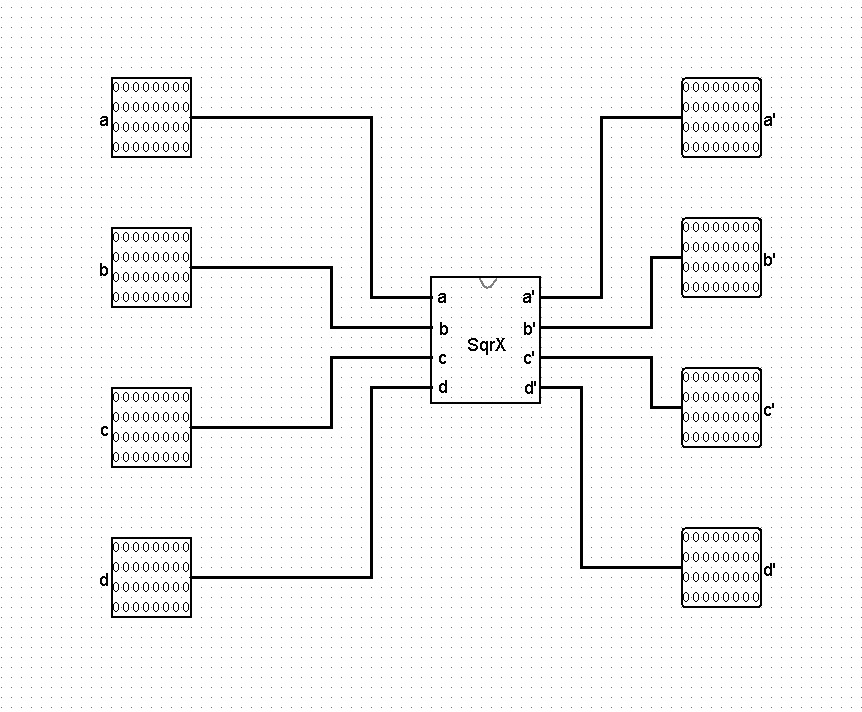
-
计算矩阵 X2·A 模块
要求:
-
给出矩阵 X2·A 计算模块的设计思路;
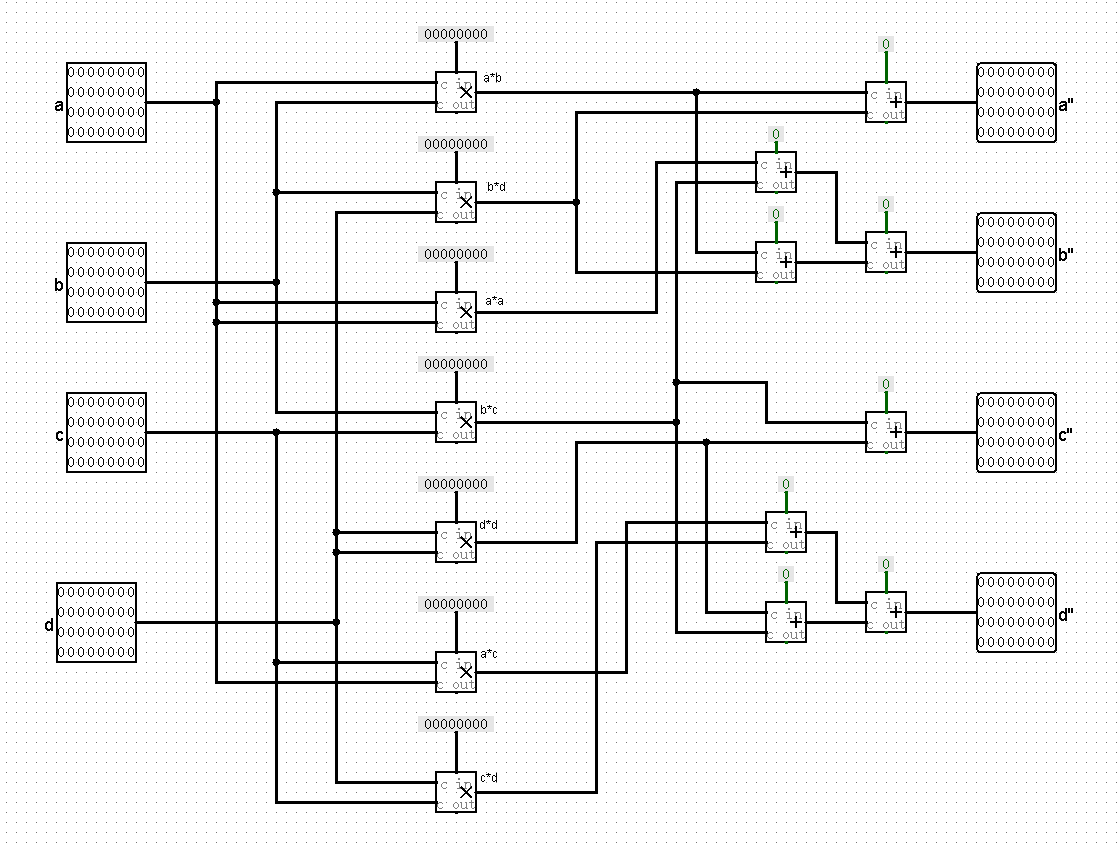
输入为 a,b,c,d,输出为 a’’,b’’,c’’,d’’,其中
a″ = ab+bd
b″ = a2+bc+ab+bd
c″ = bc+d2
d″ = ac+cd+bc+d2
根据输出与输入的关系,用乘法器和加法器连接即可。
-
给出 logisim 软件绘制的电路图(经过仿真验证基本正确);
对矩阵 X2·A 模块进行封装,给出封装后的模块图。
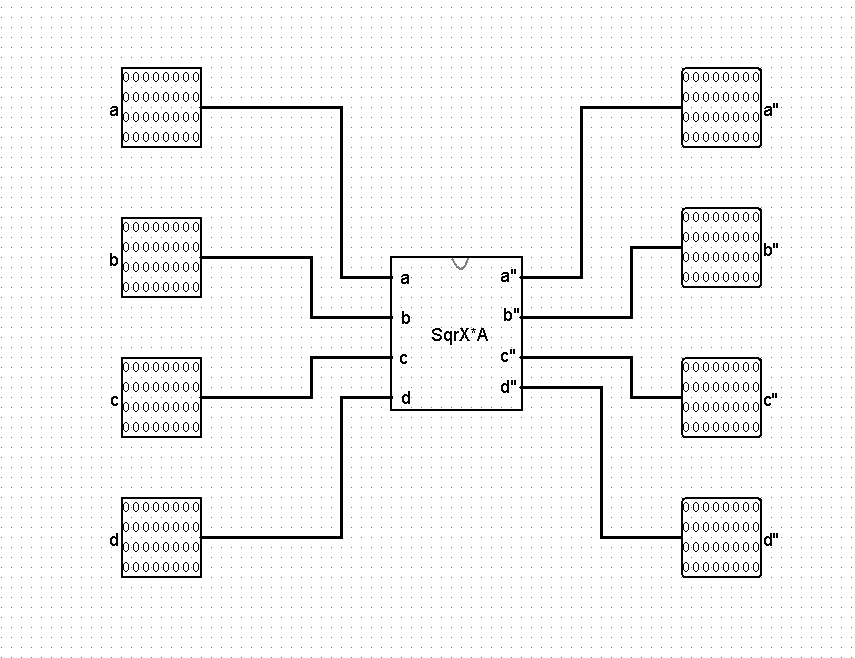
-
矩阵快速幂算法迭代模块设计
要求:
-
给出矩阵快速幂算法迭代模块设计思路;
利用四个多路选择器,当 start 为 0,输入初始矩阵{0,1,1,1},为 1 时输入上一步的结果,接着用四个寄存器存储多路选择器的值,当时钟来时将值传给下一步,再用四个多路选择器根据 ni-1 的值选择矩阵计算模块,其中,start 信号后加两个缓冲器确保清零功能正常。
-
给出 logisim 软件绘制的电路图(经过仿真验证基本正确);
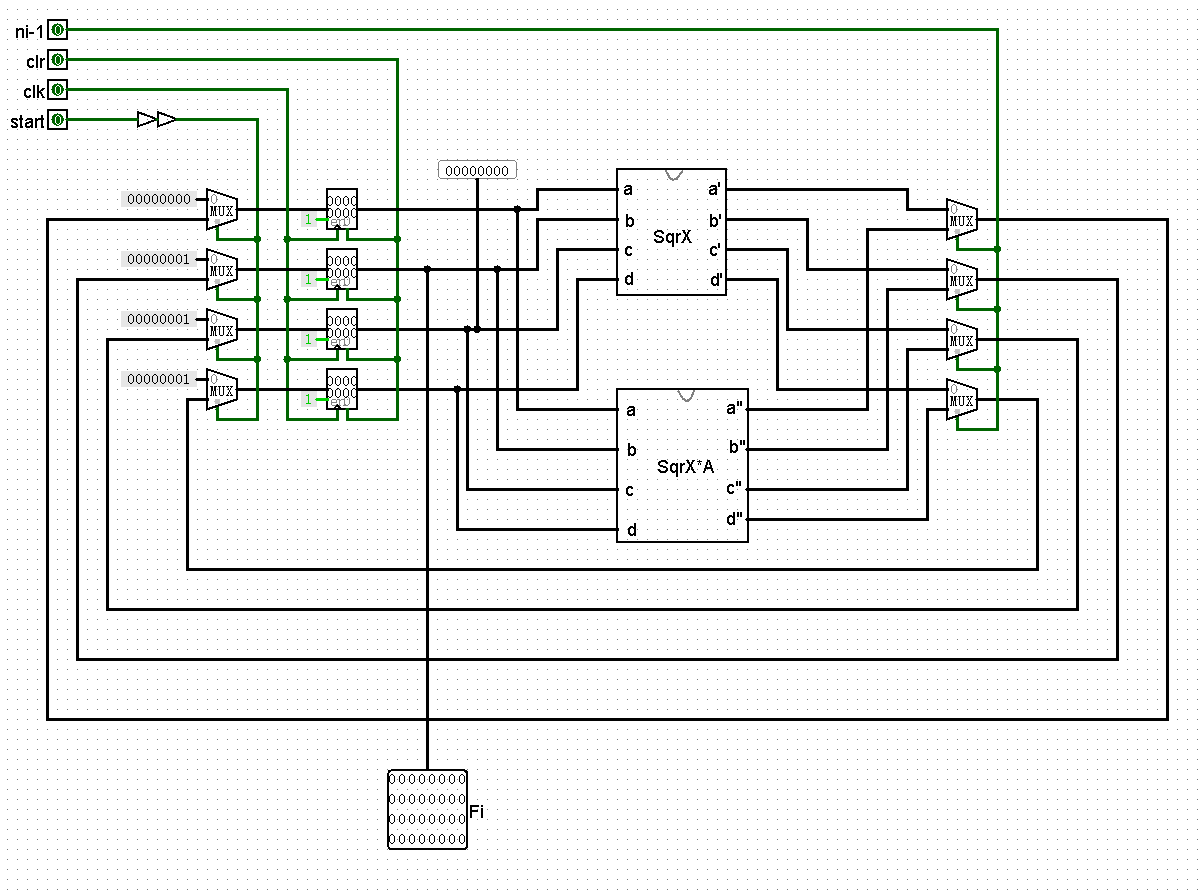
对矩阵 X2·A 模块进行封装,给出封装后的模块图。
-
主模块 main 设计
要求:
-
说明主模块 main 中控制和显示部分的设计思路;
控制:将 n 的每一位扩展成 6 位送给移位器的输入,并在 clear 信号给移位器的加载端和移位端的分支加两个缓冲器确保移位器存储值正常更新。利用计数器和比较器,当接受 6 个脉冲后,小于端输出为 0,跟时钟端通过与门连接,这样时钟无法通过。利用 D 触发器和或门,当 start 值为 1 时,保证 D 一直为 1,直到 clear 信号。
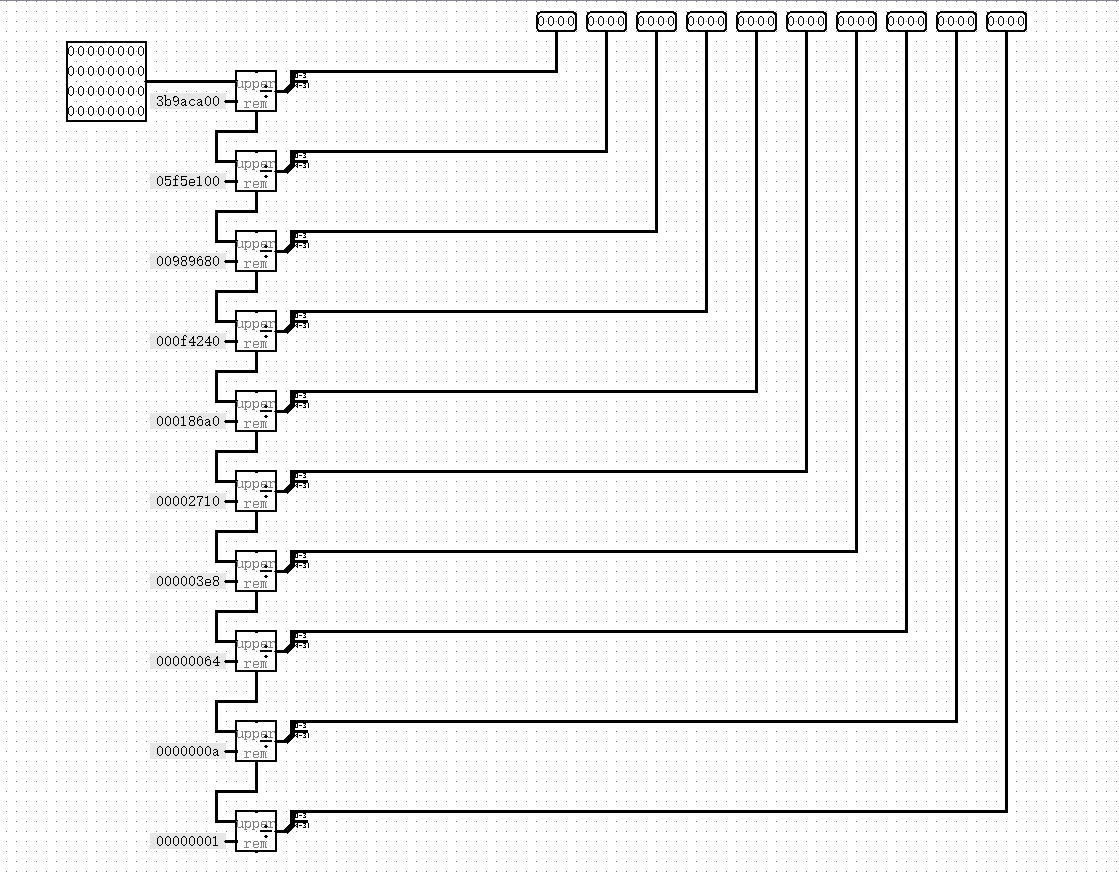
显示:采用除 10 取余法将结果转化为 10 进制数,输入为 Fi,输出为 10 组 8421BCD 码,串联 10 个除法器,每个除法器的被除数为上一个的商,余数即为该组 8421BCD 码。
-
给出主模块的 logisim 软件绘制的电路图(经过仿真验证基本正确)。
6. 实验结果记录
根据下表中所列内容,记录相应信号作用后输出数码管显示数据,并填入表 1 中(注:要求 clear、clock 使用按钮输入)。
| Input n | clear | 1st clock | 2nd clock | 3rd clock | 4th clock | 5th clock | 6th clock | After; 6th clock |
|---|---|---|---|---|---|---|---|---|
| 2 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | 0 | 1 | 1 | 1 | 1 | 1 | 5 | 5 |
| 10 | 0 | 1 | 1 | 1 | 1 | 5 | 55 | 55 |
| 17 | 0 | 1 | 1 | 1 | 3 | 21 | 1597 | 1597 |
| 25 | 0 | 1 | 1 | 2 | 8 | 144 | 75025 | 75025 |
| 32 | 0 | 1 | 1 | 3 | 21 | 987 | 2178309 | 2178309 |
| 44 | 0 | 1 | 1 | 5 | 89 | 17711 | 701408733 | 701408733 |
| 45 | 0 | 1 | 1 | 5 | 89 | 17711 | 1134903170 | 1134903170 |
| 46 | 0 | 1 | 1 | 5 | 89 | 28657 | 1836311903 | 1836311903 |
| 47 | 0 | 1 | 1 | 5 | 89 | 28657 | 2971215073 | 2971215073 |
7. 实验中遇到的问题及解决方法
7.1 故障 1
- 问题描述:清零出现错误,不能输出 0
- 问题分析:start 和 clear 信号同时到,导致寄存器输出的值并不是 0,二是前面的数据选择器组的值
- 解决方法:如图 4-15
由控制模块产生 start 和 ni-1,控制模块基本不变,修改计算模块,输入 a 和 b,计算 t1 和 t2,由 ni-1 的值选择 a=t1,b=t2。
-
请谈谈对用硬件和用软件实现同一算法的优势和劣势。
硬件实现一般效率更高,但难以更改,成本较高;
软件实现效率比硬件实现要低,但易修改,成本低。
资源下载地址:https://download.csdn.net/download/sheziqiong/85734538
资源下载地址:https://download.csdn.net/download/sheziqiong/85734538
最后
以上就是清爽柜子最近收集整理的关于斐波那契(Fibonacci)数列计算器设计的全部内容,更多相关斐波那契(Fibonacci)数列计算器设计内容请搜索靠谱客的其他文章。








发表评论 取消回复