曲率知识总结
- Introduction
- 弧微分
- 弧长公式
- 曲率与曲率半径
- 曲率
- 曲率半径
- References
Introduction
NULL
弧微分
设函数f(x)在区间(a,b)内具有连续导数,图形如图2.1中
A
B
^
widehat{AB}
AB
所示.
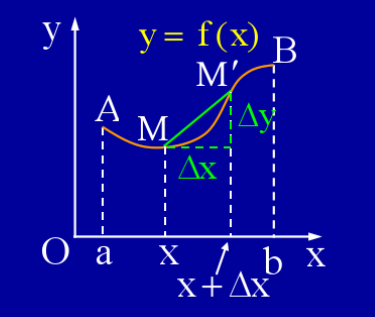
现在存在一段弧s, s ( x ) = A M ^ s(x) = widehat{AM} s(x)=AM .则曲线s从M到M’点关于x的变化率为 d s d x frac{ds}{dx} dxds:
d s d x = M M ′ ^ Δ x = M M ′ ^ ∣ M M ′ ∣ ∗ ∣ M M ′ ∣ Δ x = M M ′ ^ ∣ M M ′ ∣ ∗ ( Δ x ) 2 + ( Δ y ) 2 Δ x frac{ds}{dx}=frac{widehat{MM'}}{Delta x}=frac{widehat{MM'}}{|MM'|} * frac{|MM'|}{Delta x}= frac{widehat{MM'}}{|MM'|} * frac{sqrt{(Delta x)^2 + (Delta y)^2}}{Delta x} dxds=ΔxMM′ =∣MM′∣MM′ ∗Δx∣MM′∣=∣MM′∣MM′ ∗Δx(Δx)2+(Δy)2
因为 lim Δ x → 0 M M ′ ^ ∣ M M ′ ∣ = 1 lim_{Delta x to 0}frac{widehat{MM'}}{|MM'|} = 1 limΔx→0∣MM′∣MM′ =1
所以 lim Δ x → 0 M M ′ ^ ∣ M M ′ ∣ ∗ ( Δ x ) 2 + ( Δ y ) 2 Δ x = ( Δ x ) 2 + ( Δ y ) 2 Δ x = 1 + ( Δ y Δ x ) 2 lim_{Delta x to 0}frac{widehat{MM'}}{|MM'|} * frac{sqrt{(Delta x)^2 + (Delta y)^2}}{Delta x} = frac{sqrt{(Delta x)^2 + (Delta y)^2}}{Delta x}=sqrt{1+(frac{Delta y}{Delta x})^2} limΔx→0∣MM′∣MM′ ∗Δx(Δx)2+(Δy)2=Δx(Δx)2+(Δy)2=1+(ΔxΔy)2
总结得: d s d x = 1 + ( Δ y Δ x ) 2 = 1 + ( y ′ ) 2 frac{ds}{dx}=sqrt{1+(frac{Delta y}{Delta x})^2}=sqrt{1+(y')^2} dxds=1+(ΔxΔy)2=1+(y′)2
最终得: d s = 1 + ( Δ y Δ x ) 2 d x = ( d x ) 2 + ( d y ) 2 = 1 + ( y ′ ) 2 d x ds=sqrt{1+(frac{Delta y}{Delta x})^2}dx = sqrt{(dx)^2+(dy)^2}= sqrt{1+(y')^2}dx ds=1+(ΔxΔy)2dx=(dx)2+(dy)2=1+(y′)2dx
使用参数方程表示时:
{
x
=
X
(
t
)
y
=
Y
(
t
)
left{begin{matrix}\x = X(t)\y = Y(t)\end{matrix}right.
{x=X(t)y=Y(t)
d d t X ( t ) = X ′ ( t ) = x ′ = d x d t frac{mathrm{d}}{mathrm{d}t}X(t) = X'(t) = x' = frac{dx}{dt} dtdX(t)=X′(t)=x′=dtdx
d d t Y ( t ) = Y ′ ( t ) = y ′ = d y d t frac{mathrm{d}}{mathrm{d}t}Y(t) = Y'(t) = y' = frac{dy}{dt} dtdY(t)=Y′(t)=y′=dtdy
最终得: d s = ( X ′ ) 2 + ( Y ′ ) 2 d t ds=sqrt{(X')^2+(Y')^2}dt ds=(X′)2+(Y′)2dt
弧长公式
由弧微分公式可以推导出弧长的计算公式:
1. 当使用一般形式
y
=
f
(
x
)
,
s
y = f(x), s
y=f(x),s表示方程走过的路径时,
s
s
s是关于x的积分:
∫ a u d s = ∫ a u 1 + ( y ′ ) 2 d x int_{a}^{u}ds = int_{a}^{u}sqrt{1+(y')^2}dx ∫auds=∫au1+(y′)2dx
s ( u ) = ∫ a u 1 + ( y ′ ) 2 d x s(u) = int_{a}^{u}sqrt{1+(y')^2}dx s(u)=∫au1+(y′)2dx
2. 使用参数方程时, s s s是关于t的积分:
s ( u ) = ∫ a u ( X ′ ) 2 + ( Y ′ ) 2 d t s(u) = int_{a}^{u}sqrt{(X')^2+(Y')^2}dt s(u)=∫au(X′)2+(Y′)2dt
还有使用向量函数的表现形式,这里先不表。
曲率与曲率半径
曲率
如图3.1所示,在一段弧线上,从点M开始,取距离为
Δ
s
Delta s
Δs, 切线转角为
Δ
α
Delta alpha
Δα的位移到达
M
′
M'
M′,则定义弧段
Δ
s
Delta s
Δs上的平均曲率
K
‾
=
∣
Δ
α
Δ
s
∣
overline{K} = |frac{Delta alpha }{Delta s}|
K=∣ΔsΔα∣,定义在点M处的曲率为
K
=
lim
Δ
s
→
0
∣
Δ
α
Δ
s
∣
=
∣
d
α
d
s
∣
K=lim_{Delta s to 0}|frac{Delta alpha }{Delta s}| = |frac{dalpha }{ds}|
K=limΔs→0∣ΔsΔα∣=∣dsdα∣。

曲率公式推导:
设曲线弧 y = f ( x ) y =f(x) y=f(x)二阶可导,曲线在一点处的切线角为 α alpha α,可知在一点处的斜率可表示为 y ′ = d y d x = t a n ( α ) y' = frac{dy}{dx} = tan (alpha) y′=dxdy=tan(α),从而可得
α = a r c t a n ( y ′ ) alpha = arctan(y') α=arctan(y′)。
d α d x = ( a r c t a n ( y ′ ) ) ′ y ′ ′ = y ′ ′ 1 + ( y ′ ) 2 frac{dalpha }{dx} = (arctan(y'))'y'' = frac{y''}{1 + (y')^2} dxdα=(arctan(y′))′y′′=1+(y′)2y′′
因为 d s = 1 + ( y ′ ) 2 d x ds=sqrt{1+(y')^2}dx ds=1+(y′)2dx
所以 d α = y ′ ′ ( 1 + ( y ′ ) 2 ) 3 2 d s dalpha = frac{y''}{(1 + (y')^2)^{frac{3}{2}}}ds dα=(1+(y′)2)23y′′ds, K = ∣ d α d s ∣ = ∣ y ′ ′ ( 1 + ( y ′ ) 2 ) 3 2 ∣ K = |frac{dalpha }{ds}| = | frac{y''}{(1 + (y')^2)^{frac{3}{2}}}| K=∣dsdα∣=∣(1+(y′)2)23y′′∣。
使用参数方程表示时:
{ x = X ( t ) y = Y ( t ) left{begin{matrix}\x = X(t)\y = Y(t)\end{matrix}right. {x=X(t)y=Y(t)
K
=
∣
d
α
d
s
∣
=
∣
X
′
Y
′
′
−
X
′
′
Y
′
(
(
X
′
)
2
+
(
Y
′
)
2
)
3
2
∣
K = |frac{dalpha }{ds}| = | frac{X'Y''-X''Y'}{((X')^2 + (Y')^2)^{frac{3}{2}}}|
K=∣dsdα∣=∣((X′)2+(Y′)2)23X′Y′′−X′′Y′∣
过程参照:https://blog.csdn.net/buaazyp/article/details/82622972
曲率半径
曲率的倒数就是曲率半径。
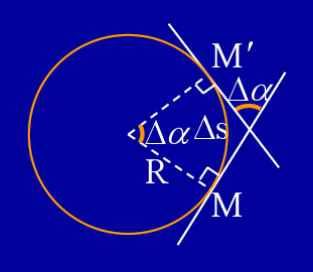
如上图所示, Δ s = R Δ α Delta s = RDelta alpha Δs=RΔα
所以 K = lim Δ s → 0 ∣ Δ α Δ s ∣ = 1 R K = lim_{Delta s to 0}|frac{Delta alpha }{Delta s}| = frac{1}{R} K=limΔs→0∣ΔsΔα∣=R1。
最终得 R = 1 K R = frac {1}{K} R=K1。
由这一性质得,曲率越大,其对应的圆越小,曲率半径越小,相反的,曲率越小,其对应的圆越大,曲率半径越大。
References
-
https://wenku.baidu.com/view/92af806c26d3240c844769eae009581b6bd9bdb5.html
-
https://baike.baidu.com/item/%E6%9B%B2%E7%8E%87%E5%8D%8A%E5%BE%84/2036643
-
https://blog.csdn.net/buaazyp/article/details/82622972
最后
以上就是激动饼干最近收集整理的关于曲率知识总结Introduction弧微分弧长公式曲率与曲率半径References的全部内容,更多相关曲率知识总结Introduction弧微分弧长公式曲率与曲率半径References内容请搜索靠谱客的其他文章。








发表评论 取消回复