极限 limitation

极限存在的充要条件:
$$\underset{x->x_0}{\lim }f(x)=A的充要条件是\underset{x->x_0^{-}}{\lim }f(x)=\underset{x->x_0^{+}}{\lim }f(x)=A$$,即左极限=右极限.

• 连续
  $f(x)在x=x_0$处连续的定义为:$$\underset{x->x_0}{\lim }f(x)=f(x_0)$$

导数 derivative

对于函数$y=f(x)$,导数的定义是 $$f^{\prime }(x_0)=\underset{\Delta x->0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\text{\hspace{1em}(1)}$$
可以看到它本质是一个极限, 是标量, 其几何意义为 点$x_0$处的斜率.

偏导数

自变量扩展为多元 $x$ 时, 可对某一维 $x_i$ 单独计算其导数$\frac{\partial f}{\partial x_i}$, 称为 偏导数.

方向导数

directional derivative. 很多时候, 仅有坐标轴方向上的偏导数是不够的, 我们还想知道任意方向上的导数, 称为 方向导数. 方向导数是矢量.
空间中的任意方向, 是可以用各坐标轴对应的基向量, 通过线性组合表示的. 同理, 方向导数可由各个维度的偏导数组合而来.

梯度

梯度是矢量, 指向函数增长最快的方向. 其模表示斜率的大小.
深度学习中要求的是损失函数的最小值, 就是要沿着梯度的反方向迭代.

求导法则

• 函数的 加,减,积,商 求导
  $u,v$ 分别是两个可导函数.
  $(u\pm v{)}^{\prime }=u^{\prime }\pm v^{\prime }$
  $(uv{)}^{\prime }=u^{\prime }v+v^{\prime }u$
  $(\frac{u}{v}{)}^{\prime }=\frac{u^{\prime }v-v^{\prime }u}{v^2}$

• 反函数的导数
  略

• 复合函数的导数
  如果$u=\phi (x)$ 在点$x_0$ 处可导, $y=f(u)$ 在点$u_0=\phi (x_0)$ 处可导, 那么复合函数$y=f[\phi (x)]$ 在点$x_0$ 处可导, 导数为:
  $$\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}$$
  复合函数的求导法则亦称为链式法则.
  例题:
  $$\frac{d[(1-2x{)}^{100}]}{dx}=\frac{d[(1-2x{)}^{100}]}{d(1-2x)}\cdot \frac{d(1-2x)}{dx}=-200(1-2x{)}^{99}$$

常用公式

$(x^a{)}^{\prime }=a{x}^{a-1}$
$(a^x{)}^{\prime }=a^{x}lna$
$(\sin x{)}^{\prime }=\cos x$

二阶偏导

如果函数f连续，则二阶偏导数的求导顺序没有区别，即$\frac{\partial }{\partial x}(\frac{\partial f}{\partial y})=\frac{\partial }{\partial y}(\frac{\partial f}{\partial x})$

• 梯度
  $$\nabla f(x)=(\frac{\partial f(x)}{\partial x_1},...,\frac{\partial f(x)}{\partial x_n}{)}^T$$
• 黑塞矩阵
  黑塞矩阵为n阶方阵${\nabla }^{2}f(\mathbf{x})$,第ij元$[{\nabla }^{2}f(\mathbf{x}){]}_{ij}=\frac{{\partial }^{2}f(\mathbf{x})}{\partial x_i\partial x_j}$, 展开后见下:
  

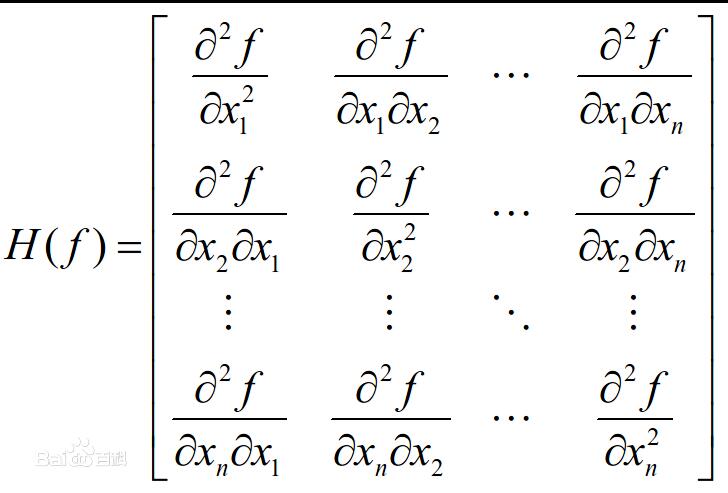
机器学习中的梯度计算

见参考[1].

参考

1. 机器学中的梯度下降与最优化求解
   

最后

以上就是自由冷风最近收集整理的关于极限, 微分,导数与梯度极限 limitation导数 derivative求导法则常用公式二阶偏导机器学习中的梯度计算参考的全部内容，更多相关极限,内容请搜索靠谱客的其他文章。