补2017.11.12日:-10
第一节 微分中值定理
》费马引理与驻点

旁白:如果以二次函数做比方,其几何意义就是二次函数曲线中的最高点和最低点,斜率为0,临域内的值要么始终不小于,要么始终不大于它,该点称之为函数的驻点。
》罗尔定理

旁白:很明显罗尔定理在费马引理的基础上进行了延伸,提供了驻点存在的证明手法,但是这个f(a)=f(b)的条件非常苛刻。
》拉格朗日中值定理(微分中值定理)

旁白:光这么看可能没感觉,书中的这幅图能加深理解。
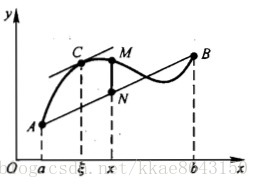
看了这幅图,然后看上面那个等式,这个定理其实是罗尔定理的加强版,一定存在与AB两点相连线段斜率一致的点。而罗尔定理就是其中的一种情况,斜率为0.
》微分中值定理逆命题

》柯西中值定理

旁白:柯西中值定理很明显又是一个加强版,如果将y与x的函数,分解为参数函数y=f(t),x=f(t)。那么拉格朗日中值定理就会演变成柯西中值定理。
补2017.11.14日:-9
第二节 洛必达法则
》未定式
还记得一脸懵逼的0/0,∞/∞么。

》洛必达法则

旁白:因此又多了一种求极限的手段,化成一脸懵逼的0/0或者∞/∞,然后用洛必达法则求极限。好吧,有点怕
补2017.11.16日:-7
第三节 泰勒公式
旁白:这节有点难,容我慢慢道来。
》公式由来
旁白:还记得微分一节中我们通过微分可以进行误差估计吗?△y=A*△x+o(△x),这里△x的高阶无穷小就是误差,但是其实还能细分,o(△x)可能包括1阶2阶3阶….n阶无穷小,如果要求误差精确到n阶无穷小,那么就不能采用微分的估计方式了,必须采用高次多项式来表达。
》公式提出
旁白:就是对于f(x)进行估计的时候,提出一个函数p(x),要求f(x)与p(x)的差距是△x的(n+1)阶无穷小,这时候就能保证误差精度在n阶无穷小以内,令△x=x-x0
》推导公式
根据以上规则f(x)=p(x)+o((x-x0)^n),所以f(x)的n阶以内的导数在x=x0时,都跟p(x)的相等(高阶的都为0)
》泰勒中值定理

旁白:看懂了上面的推导公式,再看泰勒中值定理的证明就不难了,主要重复利用柯西中值定理以及Rn(x)的n阶导数在x0处都为0的特性。

》泰勒公式误差估计

》另一种表示方法:佩亚诺余项

》简化公式:麦克劳林公式

旁白:公式太复杂,要自己动手算算才行。看完它今天都没想法看数学了囧
补2017.11.18日:-5
第四节 函数单调性与曲线凹凸性
旁白:看完上一节再来看这一节就比较轻松了,呼呼
》一阶导数与单调性

》二阶导数与凹凸性

旁白:这个也好理解,前面探讨过的瞬时速度就是路程s关于时间t的一阶导数,速度正负决定了s接下来是变大还是变小,反映在图上就是曲线会上升还是下降也就是增或减。而速度v关于t的一阶导数,也就是路程s关于t的二阶导数,反映了速度接下来是上升还是下降,速度上升,路程s会更加快速上升,反应在图上就是凹陷的。
》拐点
当曲线经过某点时其凹凸性发生变化,那么该点称之为拐点。
旁白:很明显拐点出现的时候二阶导数一定为0,先求二阶导数为0的时候,然后再来求左边和右边的凹凸性即可。
补2017.11.19日:-3
第五节 函数极值与最值
》极值
旁白:极值说简单点,就是某一狭小区域里的最值。但是对于整个大区域,该极值不一定是最值。
》极值点定理1

旁白:这里强调是必要条件,说明光靠导数为0还不能证明是极值点,因为曲线有可能是递减或者递增的,只不过凹凸性发生了变化。
》极值点定理2

》极值点定理3

补2017.11.21日:-10
第六节 函数图形的描绘
》利用导数描绘图形

旁白:这节没有什么可聊,就是利用导数来画函数曲线
补2017.11.23日:-14
第七节 曲率
第八节 方程的近似解
这两节看着好没兴趣,先丢一边
最后
以上就是傻傻胡萝卜最近收集整理的关于高等数学复习之三(微分中值定理与导数应用)的全部内容,更多相关高等数学复习之三(微分中值定理与导数应用)内容请搜索靠谱客的其他文章。

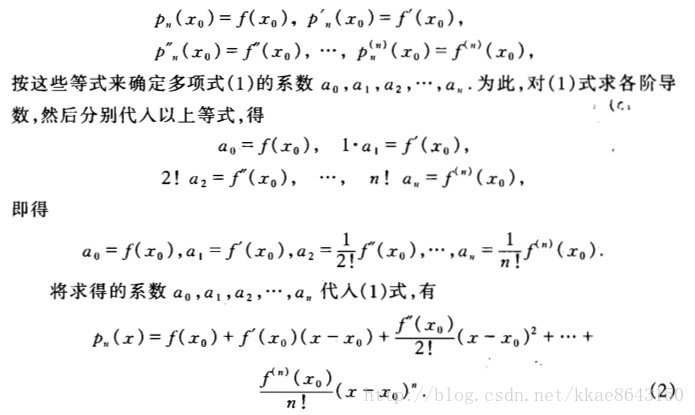








发表评论 取消回复