文章目录
- #常用极限
- #常用级数
- #常用求导
- #求导的注意事项
欢迎纠错
常用极限,导数,级数
秒杀必背积分表实数部分
秒杀必背积分表三角部分
#常用极限
lim x → 0 sin x x = 1 lim n → ∞ ( 1 + 1 n ) n = e ; lim x → ∞ ( 1 + 1 x ) x = e lim_{xto 0}frac{sin x}{x}=1\ \ lim_{nto infty}(1+frac 1 n)^n=espace;spacelim_{xto infty}(1+frac 1 x)^x=e x→0limxsinx=1 n→∞lim(1+n1)n=e ; x→∞lim(1+x1)x=e
当 x → 0 : sin x → x ; tan x → x ; arctan x → x ; arcsin x → x ; 1 − cos x → x 2 2 ; 1 + x n → 1 n x ; e x − 1 → x ; ln ( x + 1 ) → x ; ( 1 + x ) α → α x ; ln ( x + 1 + x 2 ) → x log a ( 1 + x ) → x ln a ; a x − 1 → x ln a x − sin x → 1 6 x 3 ; tan x − x → 1 3 x 3 arcsin x − x → 1 6 x 3 ; x − arctan x → 1 3 x 3 tan x − sin x → 1 2 x 3 1 − 1 − x 2 → 1 2 x 2 1 + x a − 1 → 1 2 x a 当xto 0:\ \ sin xto xspacespace;spacespacetan xto xspacespace;\ \arctan xto xspacespace;spacespacearcsin xto xspacespace;\ \ 1-cos xto frac{x^2}2spacespace;spacespacesqrt[n]{1+x}to frac 1 n xspacespace;\ \ e^x-1to xspacespace;spacespaceln(x+1)to xspacespace;\ \ (1+x)^alphato alpha xspacespace;spacespaceln (x+sqrt{1+x^2})to x\ \ log_a(1+x)tofrac x{ln a}spacespace;spacespace a^x-1to xln a\ \ x-sin xtofrac 1 6x^3 spacespace;spacespace tan x-xto frac 1 3 x^3\ \ arcsin x -xto frac 1 6 x^3 spacespace;spacespace x-arctan xtofrac 1 3 x^3\ \ tan x-sin xto frac 1 2 x^3\ \1-sqrt{1-x^2}tofrac 1 2 x^2\ \sqrt{1+x^a}-1tofrac 1 2 x^a 当x→0: sinx→x ; tanx→x ; arctanx→x ; arcsinx→x ; 1−cosx→2x2 ; n1+x→n1x ; ex−1→x ; ln(x+1)→x ; (1+x)α→αx ; ln(x+1+x2)→x loga(1+x)→lnax ; ax−1→xlna x−sinx→61x3 ; tanx−x→31x3 arcsinx−x→61x3 ; x−arctanx→31x3 tanx−sinx→21x3 1−1−x2→21x2 1+xa−1→21xa
lim x → 0 sin 1 x 1 x = 0 lim_{xto 0}frac{sin frac 1 x}{frac 1 x}=0 x→0limx1sinx1=0
#常用级数
1 1 − z = ∑ n = 0 ∞ z n = 1 + z + z 2 ⋯ + z n + ⋯ 1 1 + z = ∑ n = 0 ∞ ( − 1 ) n z n = 1 − z + z 2 ⋯ + ( − 1 ) n z n + ⋯ ln ( 1 + x ) = x − x 2 2 + x 3 3 − ⋯ + ( − 1 ) n x n + 1 n + 1 + ⋯ e x = 1 + x + x 2 2 + ⋯ + x n n ! + ⋯ sin x = x − x 3 3 ! + x 5 5 ! − ⋯ + ( − 1 ) n + 1 x 2 n − 1 ( 2 n − 1 ) ! + ⋯ cos x = 1 − x 2 2 ! + x 4 4 ! − ⋯ + ( − 1 ) n + 1 x 2 n − 2 ( 2 n − 2 ) ! + ⋯ ( 1 + x ) α = 1 + α x + α ( α − 1 ) 2 x 2 + ⋯ 1 + x 2 = 1 + 1 2 x 2 − 1 8 x 4 + o ( x 4 ) frac 1 {1-z}=sum_{n=0}^{infty}z^n=1+z+z^2cdots+z^n+cdots\ \ frac 1 {1+z}=sum_{n=0}^{infty}(-1)^nz^n=1-z+z^2cdots+(-1)^nz^n+cdots\ \ ln(1+x)=x-frac{x^2}2+frac{x^3}3-cdots+(-1)^nfrac{x^{n+1}}{n+1} +cdots\ \ e^x=1+x+frac{x^2}2+cdots+frac{x^n}{n!}+cdots\ \ sin x=x-frac{x^3}{3!}+frac{x^5}{5!}-cdots+(-1)^{n+1}frac{x^{2n-1}}{(2n-1)!}+cdots\ \ cos x=1-frac{x^2}{2!}+frac{x^4}{4!}-cdots+(-1)^{n+1}frac{x^{2n-2}}{(2n-2)!}+cdots\ \ (1+x)^alpha=1+alpha x+frac{alpha(alpha-1)}2x^2+cdots\ \ sqrt{1+x^2}=1+frac 1 2x^2-frac 1 8x^4+o(x^4) 1−z1=n=0∑∞zn=1+z+z2⋯+zn+⋯ 1+z1=n=0∑∞(−1)nzn=1−z+z2⋯+(−1)nzn+⋯ ln(1+x)=x−2x2+3x3−⋯+(−1)nn+1xn+1+⋯ ex=1+x+2x2+⋯+n!xn+⋯ sinx=x−3!x3+5!x5−⋯+(−1)n+1(2n−1)!x2n−1+⋯ cosx=1−2!x2+4!x4−⋯+(−1)n+1(2n−2)!x2n−2+⋯ (1+x)α=1+αx+2α(α−1)x2+⋯ 1+x2=1+21x2−81x4+o(x4)
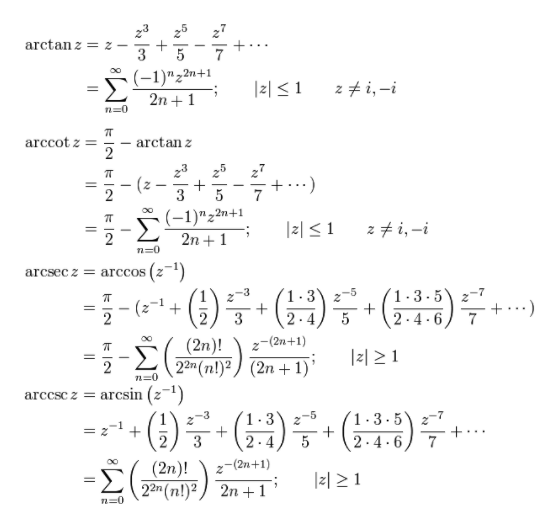
#常用求导
( arcsin x ) ′ = 1 1 − x 2 ( arccos x ) ′ = − 1 1 − x 2 ( arctan x ) ′ = 1 1 + x 2 ( a r c c o t x ) ′ = − 1 1 + x 2 ( tan x ) ′ = 1 cos 2 x = sec 2 x ( cot x ) ′ = − 1 sin 2 x = − csc 2 x ( sec x ) ′ = sec x tan x = tan x cos x ( csc x ) ′ = − csc x cot x = − 1 sin x tan x ( cos x ) ( n ) = cos ( x + n π 2 ) ( sin x ) ( n ) = sin ( x + n π 2 ) ( x n ) ( n ) = n ! ( x n ) ( n + 1 ) = 0 ( 1 x + a ) ( n ) = ( − 1 ) n n ! ( x + a ) n + 1 ( ln ( x + b ) ) ( n ) = ( − 1 ) n − 1 ( n − 1 ) ! ( x + b ) n (arcsin x)'=frac 1 {sqrt{1-x^2}}\ \ (arccos x )' =-frac 1 {sqrt{1-x^2}}\ \ (arctan x )'=frac 1 {1+x^2}\ \ (arccot x)' =-frac 1 {1+x^2}\ \ (tan x)'=frac 1 {cos^2x}=sec^2x\ \ (cot x)' =-frac 1 {sin^2 x}=-csc^2 x\ \ (sec x)'=sec xtan x=frac{tan x}{cos x}\ \ (csc x)'=-csc x cot x=-frac 1{sin x tan x}\ \ (cos x)^{(n)}=cos(x+frac {npi}2)\ \ (sin x)^{(n)}=sin(x+frac {npi}2)\ \ (x^n)^{(n)}=n! \ (x^n)^{(n+1)}=0 \ \ (frac 1 {x+a})^{(n)}=frac{(-1)^nn!}{(x+a)^{n+1}}\ \ (ln(x+b))^{(n)}=frac{(-1)^{n-1}(n-1)!}{(x+b)^{n}}\ \ (arcsinx)′=1−x21 (arccosx)′=−1−x21 (arctanx)′=1+x21 (arccotx)′=−1+x21 (tanx)′=cos2x1=sec2x (cotx)′=−sin2x1=−csc2x (secx)′=secxtanx=cosxtanx (cscx)′=−cscxcotx=−sinxtanx1 (cosx)(n)=cos(x+2nπ) (sinx)(n)=sin(x+2nπ) (xn)(n)=n!(xn)(n+1)=0 (x+a1)(n)=(x+a)n+1(−1)nn! (ln(x+b))(n)=(x+b)n(−1)n−1(n−1)!
[
f
(
x
)
⋅
g
(
x
)
]
(
n
)
=
f
(
n
)
g
+
C
n
1
f
(
n
−
1
)
g
+
⋯
+
C
n
k
f
(
n
−
k
)
g
(
k
)
+
⋯
+
f
g
(
n
)
[f(x)cdot g(x)]^{(n)}=f^{(n)}g+C_n^1f^{(n-1)}g+cdots+C_n^kf^{(n-k)}g^{(k)}+cdots+fg^{(n)}
[f(x)⋅g(x)](n)=f(n)g+Cn1f(n−1)g+⋯+Cnkf(n−k)g(k)+⋯+fg(n)
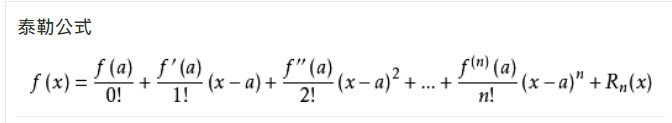
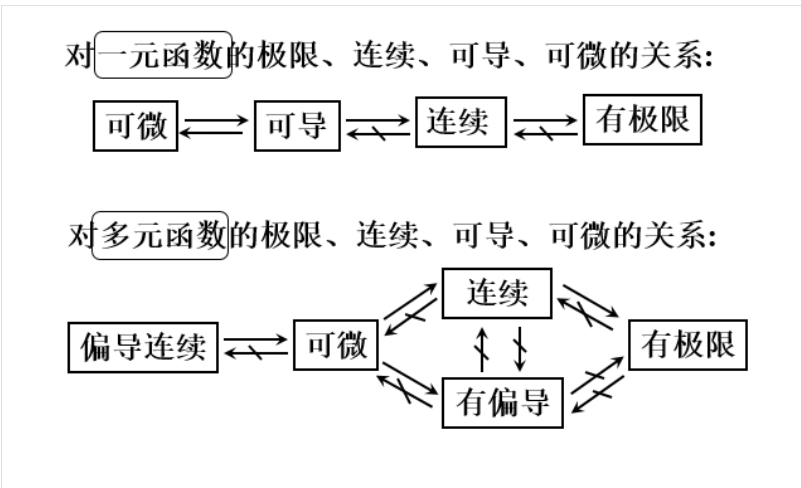
#求导的注意事项
对 于 函 数 , 其 输 入 的 变 量 之 间 必 须 相 互 独 立 对于函数,其输入的变量之间必须相互独立 对于函数,其输入的变量之间必须相互独立
因
此
,
对
于
以
坐
标
为
输
入
变
量
的
多
元
函
数
,
如
(
ρ
,
ϕ
,
z
)
,
(
r
,
θ
,
ϕ
)
其
任
意
两
个
微
商
∂
ρ
∂
ϕ
=
0
,
因此,对于以坐标为输入变量的多元函数,如\ (rho,phi,z),(r,theta,phi)\ 其任意两个微商frac{partialrho}{partialphi}=0,
因此,对于以坐标为输入变量的多元函数,如(ρ,ϕ,z),(r,θ,ϕ)其任意两个微商∂ϕ∂ρ=0,
全微分:

最后
以上就是无心白羊最近收集整理的关于【高等数学】常用极限、求导、级数#常用极限#常用级数#常用求导#求导的注意事项的全部内容,更多相关【高等数学】常用极限、求导、级数#常用极限#常用级数#常用求导#求导内容请搜索靠谱客的其他文章。








发表评论 取消回复