MATLAB 插值+计算离散点曲率

思路：点足够密的话直接用 diff、gradient 求曲率，稀疏的话先插值再算曲率。

公式：

点密的情况

1. 输入曲线坐标（1-2）
2. 求一、二阶导数（4-9）
3. 通过公式求得曲率（10）

x = 0:0.01:7;
y = cos(x*0.5*pi);

h1 = abs(diff(x));
h = [h1 h1(end)];
ht = h;

y1 = gradient(y)./ht;
y2 = gradient(y1)./ht;
curv = abs(y2)./sqrt((1+y1.^2).^3);

plot(x,y,'-',x,curv,'--r);
legend('Raw Data, 'Curvature','Location',"best");
grid on

图像与下文理论值图像相同 

点稀疏的情况

1. 输入散点坐标（1-2）
2. 用样条曲线（B-Spline）等方法插值得到拟合曲线（3-4）
3. diff、gradient 函数求拟合曲线的一、二阶导数（6-11）
4. 通过公式求得曲率（12）

例：余弦函数取 8 个点，用 B-Spline 插值

x = 0:1:7;
y = cos(x*0.5*pi);
xx = 0:0.01:7;
yy = spline(x,y,xx);

h1 = abs(diff(xx));
h = [h1 h1(end)];
ht = h;

yy1 = gradient(yy)./ht;
yy2 = gradient(yy1)./ht;
curv = abs(yy2)./sqrt((1+yy1.^2).^3);

plot(xx,yy,'-',xx,curv,'--r',x,y,'o-');
legend('B-Spline', 'Curvature','Raw Data','Location',"best");
grid on

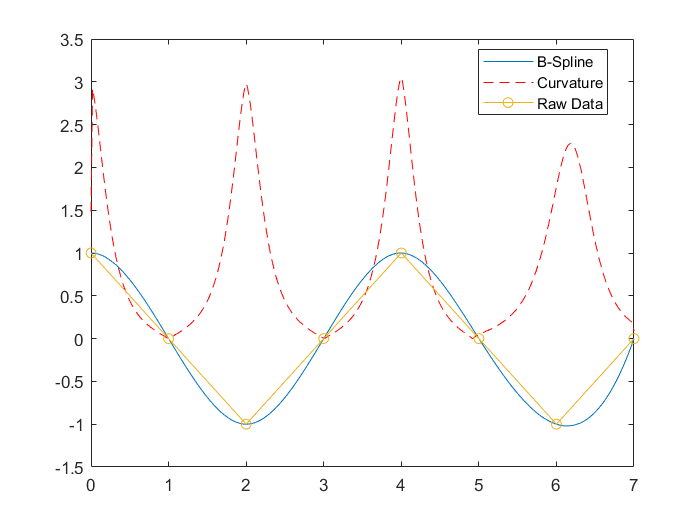
补充用法

求最大曲率并在图中标出

[max_val,max_ind]=max(curv);
hold on
plot(xx(max_ind),yy(max_ind),'*r');

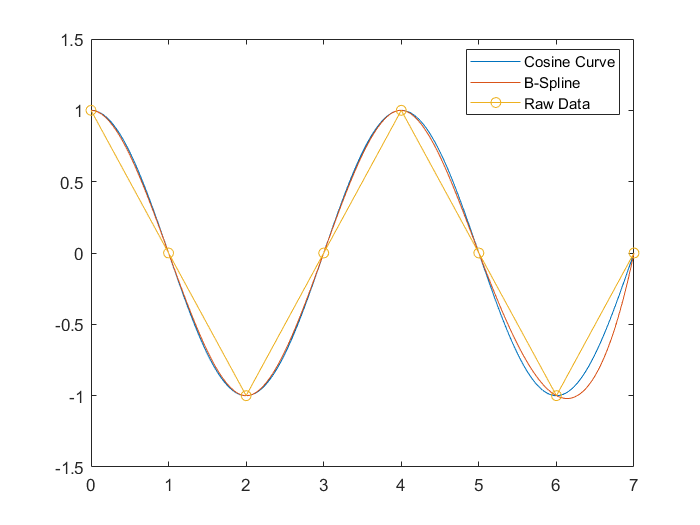
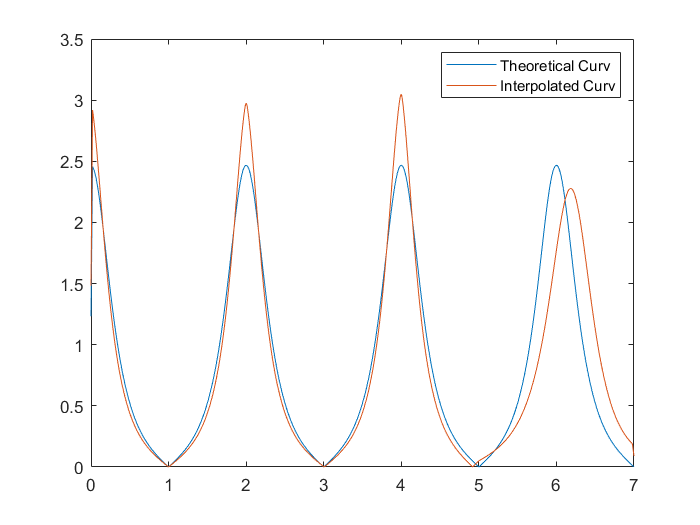
与理论值（余弦函数曲线）对比

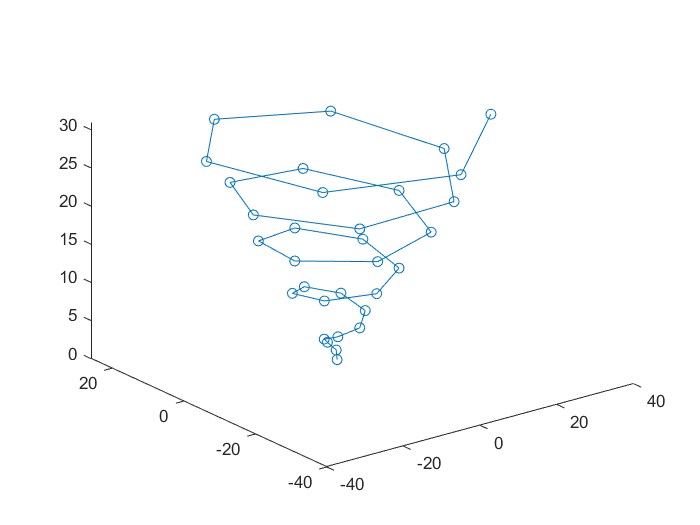
几种插值方法对比

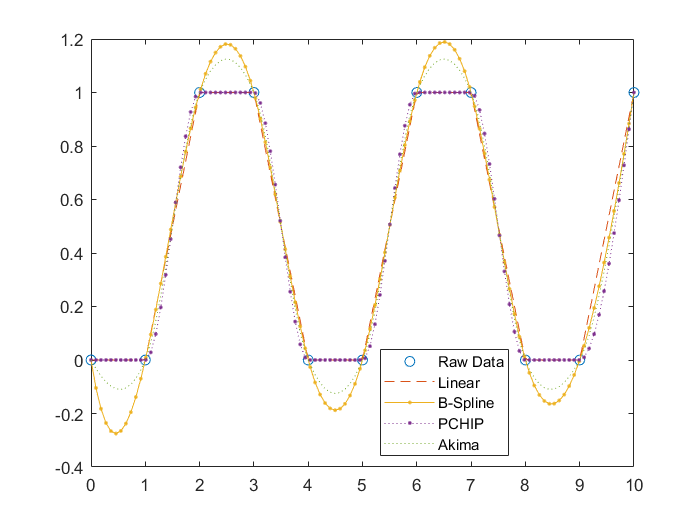
列举四种方法，分别为：分段线性插值、三次样条曲线（B-Spline）插值、三次 Hermite 插值（PCHIP）、修正 Akima 分段三次 Hermite 插值（Akima）

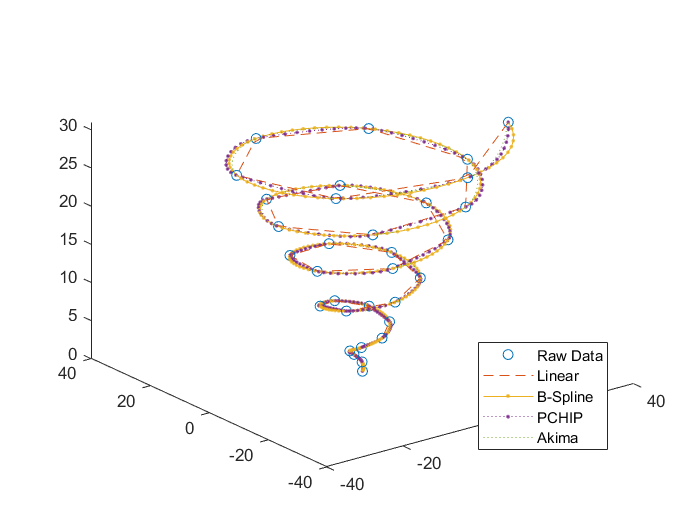
Case 1： 三维螺线

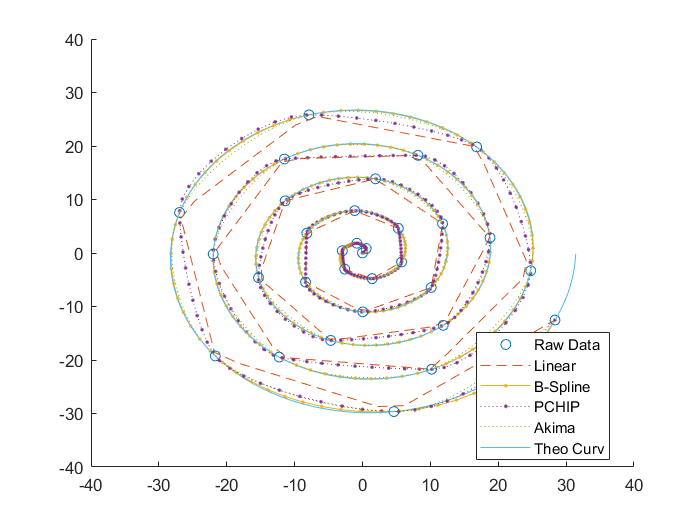
Case 2：二维梯形波

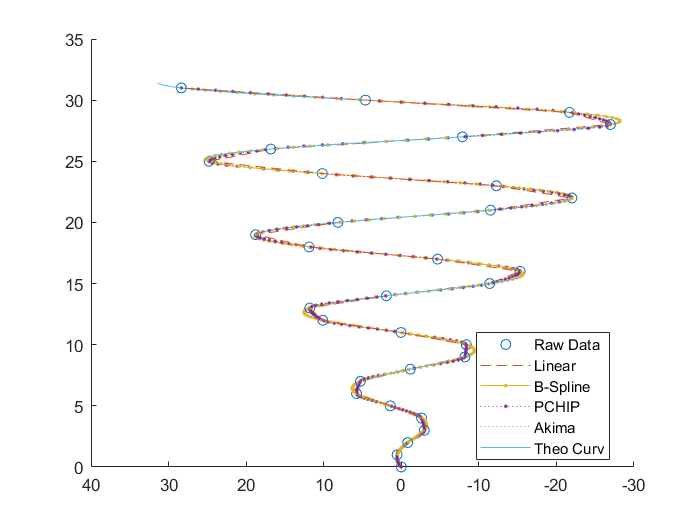
Case 3：三维不规则折线

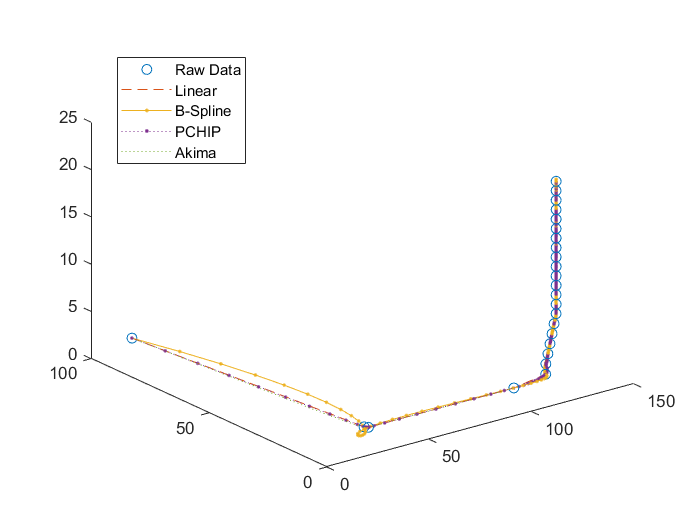
对比可得：

Case 1：B-Spline>Akima>PCHIP>Linear

Case 2：Linear>PCHIP>Akima>B-Spline

Case 3：Linear≈PCHIP≈Akima>B-Spline

故在插值的时候需要选择适合的计算方法

开坑待填

三维曲线曲率计算

其实早就写好了，但是实在懒得整理_(´ཀ`」 ∠)_

最后

以上就是开心花生为你收集整理的MATLAB 插值+计算离散点曲率的全部内容，希望文章能够帮你解决MATLAB 插值+计算离散点曲率所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。