笛卡尔坐标系与Frenet坐标系互转,可能需要曲率的导数信息。此出给出推导过程与计算式,方便以后写代码时查阅。
1. 曲线的表示形式
二维平面上的曲线有两种参数化形式,如下所示:
-
参数方程1
{ x t = x ( t ) y t = y ( t ) left{begin{matrix} x_t=x(t) \ y_t=y(t) end{matrix} right. {xt=x(t)yt=y(t) -
参数方程2
{ x t = x t y t = y ( x t ) left{begin{matrix} x_t=x_t \ y_t=y(x_t) end{matrix} right. {xt=xtyt=y(xt)
以上两种参数方程都可以唯一确定一条二维平面内的曲线。因此,下文计算的曲率、曲率的导数以及曲率导数的导数的公式都有两种等价的形式。
2. 曲率计算公式及推导
先给出熟悉的曲率计算公式:
k
=
x
′
y
′
′
−
y
′
x
′
′
(
x
′
2
+
y
′
2
)
3
2
(
对
应
参
数
方
程
1
)
(1)
k=frac{x'y''-y'x''}{(x'^{2}+y'^{2})^{frac{3}{2}}} (对应参数方程1)tag{1}
k=(x′2+y′2)23x′y′′−y′x′′(对应参数方程1)(1)以及:
k
=
y
′
′
(
1
+
y
′
2
)
3
2
(
对
应
参
数
方
程
2
)
(2)
k=frac{y''}{(1+y'^2)^{frac{3}{2}}}(对应参数方程2)tag{2}
k=(1+y′2)23y′′(对应参数方程2)(2)
2.1 参数方程1曲率公式推导
假定点
(
x
t
,
y
t
)
(x_t, y_t)
(xt,yt)处的切角为
α
alpha
α,则此点处曲线的斜率为
tan
(
α
)
tan(alpha)
tan(α)。
x
t
,
y
t
x_t,y_t
xt,yt的变量都为
t
t
t,假定
t
t
t有一个小的增量
Δ
t
Delta_t
Δt,则,
x
t
x_t
xt与
y
t
y_t
yt相应的都有一个小的增量
Δ
x
Delta_x
Δx与
Δ
y
Delta_y
Δy。如下图所示,当
Δ
t
Delta_t
Δt很小时,
Δ
y
Δ
x
≈
t
a
n
(
α
)
frac{Delta_y}{Delta_x}approx tan(alpha)
ΔxΔy≈tan(α)。
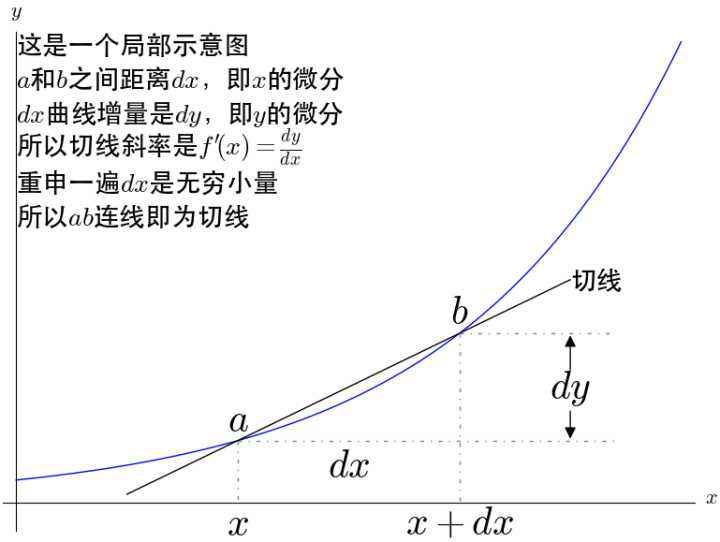
当
Δ
t
→
0
Delta_trightarrow 0
Δt→0时,
Δ
x
Delta_x
Δx与
Δ
y
Delta_y
Δy为
x
t
x_t
xt与
y
t
y_t
yt在
t
t
t处的微分,一般分别表示为
d
x
dx
dx与
d
y
dy
dy。此时有(其中
x
′
x'
x′与
y
′
y'
y′表示函数
x
(
t
)
,
y
(
t
)
x(t),y(t)
x(t),y(t)对
t
t
t的导数):
d
y
d
x
=
tan
(
α
)
⇒
d
y
d
t
d
x
d
t
=
tan
(
α
)
⇒
y
′
x
′
=
tan
(
α
)
frac{dy}{dx}=tan(alpha)Rightarrow frac{frac{dy}{dt}}{frac{dx}{dt}}=tan(alpha)Rightarrow frac{y'}{x'}=tan(alpha)
dxdy=tan(α)⇒dtdxdtdy=tan(α)⇒x′y′=tan(α)得:
y ′ x ′ = tan ( α ) frac{y'}{x'}=tan(alpha) x′y′=tan(α)
对上式两边分别求导得:
y
′
′
x
′
−
x
′
′
y
′
x
′
2
d
t
=
(
1
+
tan
2
(
α
)
)
d
α
=
(
x
′
2
+
y
′
2
x
′
2
)
d
α
frac{y''x'-x''y'}{x'^{2}}dt=(1+tan^2(alpha))dalpha=(frac{x'^2+y'^2}{x'^2})dalpha
x′2y′′x′−x′′y′dt=(1+tan2(α))dα=(x′2x′2+y′2)dα
化简得:
y
′
′
x
′
−
x
′
′
y
′
x
′
2
+
y
′
2
d
t
=
d
α
frac{y''x'-x''y'}{x'^2+y'^2}dt=dalpha
x′2+y′2y′′x′−x′′y′dt=dα
又 d s = x ′ 2 + y ′ 2 d t ds=sqrt{x'^2+y'^2}dt ds=x′2+y′2dt,代入上式得到式(1)所示的曲率计算公式(曲率为角度对弧度的导数):
k = d α d s = y ′ ′ x ′ − x ′ ′ y ′ ( x ′ 2 + y ′ 2 ) 3 2 k=frac{dalpha}{ds}=frac{y''x'-x''y'}{(x'^2+y'^2)^{frac{3}{2}}} k=dsdα=(x′2+y′2)23y′′x′−x′′y′
2.2 参数方程2曲率公式推导
此时曲线的自变量为
x
x
x,曲线在点
(
x
t
,
y
t
)
(x_t, y_t)
(xt,yt)处的导数为
y
′
=
f
′
(
x
)
=
tan
(
α
)
y'=f'(x)=tan(alpha)
y′=f′(x)=tan(α)得:
y
′
=
tan
(
α
)
y'=tan(alpha)
y′=tan(α)
对上式两边分别求导得:
y
′
′
d
x
=
(
1
+
tan
2
(
α
)
)
d
α
=
(
1
+
y
′
2
)
d
α
y''dx=(1+tan^{2}(alpha))dalpha=(1+y'^2)dalpha
y′′dx=(1+tan2(α))dα=(1+y′2)dα
化简得:
y
′
′
1
+
y
′
2
d
x
=
d
α
frac{y''}{1+y'^2}dx=dalpha
1+y′2y′′dx=dα
又 d s = 1 + y ′ 2 d x ds=sqrt{1+y'2}dx ds=1+y′2dx,代入上式得到式(2)所示的曲率计算公式:
k = y ′ ′ ( 1 + y ′ 2 ) 3 2 k=frac{y''}{(1+y'^2)^{frac{3}{2}}} k=(1+y′2)23y′′
2.3 小结
两种参数方程得到的曲率公式推导过程相似,最终公式形式也差不多。在表示曲线时,不同情况下用到的参数化方程不一样。为了简便 ,可以统一两种参数方程,令 x ( t ) = t x(t)=t x(t)=t时,参数方程1就变成了参数方程2。此时, x ′ = 1 , x ′ ′ = 0 x'=1,x''=0 x′=1,x′′=0,代入式(1)就得到式(2)。下文中,只求针对参数方程1的曲率导数 k ′ k' k′以及曲率导数的导数 k ′ ′ k'' k′′。
3. 曲率的导数(或称为变化率)公式及推导
对曲率公式 k = y ′ ′ x ′ − x ′ ′ y ′ ( x ′ 2 + y ′ 2 ) 3 2 k=frac{y''x'-x''y'}{(x'^2+y'^2)^{frac{3}{2}}} k=(x′2+y′2)23y′′x′−x′′y′两边分别求导:
k ′ = d k d s = ( y ′ ′ x ′ − x ′ ′ y ′ ) ′ ( x ′ 2 + y ′ 2 ) 3 2 − ( ( x ′ 2 + y ′ 2 ) 3 2 ) ′ ( y ′ ′ x ′ − x ′ ′ y ′ ) ( x ′ 2 + y ′ 2 ) 3 d t d s k'=frac{dk}{ds}=frac{frac{(y''x'-x''y')'(x'^2+y'^2)^{frac{3}{2}}-((x'^2+y'^2)^{frac{3}{2}})'(y''x'-x''y')}{(x'^2+y'^2)^3}dt}{ds} k′=dsdk=ds(x′2+y′2)3(y′′x′−x′′y′)′(x′2+y′2)23−((x′2+y′2)23)′(y′′x′−x′′y′)dt
将
d
s
=
x
′
2
+
y
′
2
d
t
ds=sqrt{x'^2+y'^2}dt
ds=x′2+y′2dt代入上式得:
k
′
=
(
y
′
′
′
x
′
+
y
′
′
x
′
′
−
x
′
′
′
y
′
−
x
′
′
y
′
′
)
(
x
′
2
+
y
′
2
)
3
2
−
3
2
(
x
′
2
+
y
′
2
)
1
2
(
2
x
′
x
′
′
+
2
y
′
y
′
′
)
(
y
′
′
x
′
−
x
′
′
y
′
)
(
x
′
2
+
y
′
2
)
3
(
d
t
d
s
)
=
(
x
′
2
+
y
′
2
)
1
2
[
(
y
′
′
′
x
′
−
x
′
′
′
y
′
)
(
x
′
2
+
y
′
2
)
−
3
(
x
′
x
′
′
+
y
′
y
′
′
)
(
y
′
′
x
′
−
x
′
′
y
′
)
]
(
x
′
2
+
y
′
2
)
3
1
(
x
′
2
+
y
′
2
)
1
2
=
(
y
′
′
′
x
′
+
y
′
′
x
′
′
−
x
′
′
′
y
′
−
x
′
′
y
′
′
)
(
x
′
2
+
y
′
2
)
3
2
−
3
2
(
x
′
2
+
y
′
2
)
1
2
(
2
x
′
x
′
′
+
2
y
′
y
′
′
)
(
y
′
′
x
′
−
x
′
′
y
′
)
(
x
′
2
+
y
′
2
)
3
(
d
t
d
s
)
=
(
y
′
′
′
x
′
−
x
′
′
′
y
′
)
(
x
′
2
+
y
′
2
)
−
3
(
x
′
x
′
′
+
y
′
y
′
′
)
(
y
′
′
x
′
−
x
′
′
y
′
)
(
x
′
2
+
y
′
2
)
3
k'=frac{(y'''x'+y''x''-x'''y'-x''y'')(x'^2+y'^2)^{frac{3}{2}}-frac{3}{2}(x'^2+y'^2)^{frac{1}{2}}(2x'x''+2y'y'')(y''x'-x''y')}{(x'^2+y'^2)^3}(frac{dt}{ds})\=frac{(x'^2+y'^2)^{frac{1}{2}}[(y'''x'-x'''y')(x'^2+y'^2)-3(x'x''+y'y'')(y''x'-x''y')]}{(x'^2+y'^2)^3}frac{1}{(x'^2+y'^2)^{frac{1}{2}}}\=frac{(y'''x'+y''x''-x'''y'-x''y'')(x'^2+y'^2)^{frac{3}{2}}-frac{3}{2}(x'^2+y'^2)^{frac{1}{2}}(2x'x''+2y'y'')(y''x'-x''y')}{(x'^2+y'^2)^3}(frac{dt}{ds})\=frac{(y'''x'-x'''y')(x'^2+y'^2)-3(x'x''+y'y'')(y''x'-x''y')}{(x'^2+y'^2)^3}
k′=(x′2+y′2)3(y′′′x′+y′′x′′−x′′′y′−x′′y′′)(x′2+y′2)23−23(x′2+y′2)21(2x′x′′+2y′y′′)(y′′x′−x′′y′)(dsdt)=(x′2+y′2)3(x′2+y′2)21[(y′′′x′−x′′′y′)(x′2+y′2)−3(x′x′′+y′y′′)(y′′x′−x′′y′)](x′2+y′2)211=(x′2+y′2)3(y′′′x′+y′′x′′−x′′′y′−x′′y′′)(x′2+y′2)23−23(x′2+y′2)21(2x′x′′+2y′y′′)(y′′x′−x′′y′)(dsdt)=(x′2+y′2)3(y′′′x′−x′′′y′)(x′2+y′2)−3(x′x′′+y′y′′)(y′′x′−x′′y′)
最后提取 k ′ k' k′的计算公式如下:
k ′ = ( y ′ ′ ′ x ′ − x ′ ′ ′ y ′ ) ( x ′ 2 + y ′ 2 ) − 3 ( x ′ x ′ ′ + y ′ y ′ ′ ) ( y ′ ′ x ′ − x ′ ′ y ′ ) ( x ′ 2 + y ′ 2 ) 3 ( 对 应 参 数 方 程 1 ) (3) k'=frac{(y'''x'-x'''y')(x'^2+y'^2)-3(x'x''+y'y'')(y''x'-x''y')}{(x'^2+y'^2)^3} (对应参数方程1) tag{3} k′=(x′2+y′2)3(y′′′x′−x′′′y′)(x′2+y′2)−3(x′x′′+y′y′′)(y′′x′−x′′y′)(对应参数方程1)(3)
令 x ′ = 1 , x ′ ′ = 0 , x ′ ′ ′ = 0 x'=1, x''=0, x'''=0 x′=1,x′′=0,x′′′=0代入式(3)可得参数方程2的 k ′ k' k′计算公式如下:
k ′ = y ′ ′ ′ + y ′ ′ ′ y ′ 2 − 3 y ′ y ′ ′ 2 ( 1 + y ′ 2 ) 3 ( 对 应 参 数 方 程 2 ) (4) k'=frac{y'''+y'''y'^2-3y'y''^2}{(1+y'^2)^3} (对应参数方程2)tag{4} k′=(1+y′2)3y′′′+y′′′y′2−3y′y′′2(对应参数方程2)(4)
4. 曲率导数的导数公式及推导
k ′ ′ = d k ′ d s = d ( y ′ ′ ′ x ′ − x ′ ′ ′ y ′ ) ( x ′ 2 + y ′ 2 ) − 3 ( x ′ x ′ ′ + y ′ y ′ ′ ) ( y ′ ′ x ′ − x ′ ′ y ′ ) ( x ′ 2 + y ′ 2 ) 3 d s k''=frac{dk'}{ds}=frac{dfrac{(y'''x'-x'''y')(x'^2+y'^2)-3(x'x''+y'y'')(y''x'-x''y')}{(x'^2+y'^2)^3}}{ds} k′′=dsdk′=dsd(x′2+y′2)3(y′′′x′−x′′′y′)(x′2+y′2)−3(x′x′′+y′y′′)(y′′x′−x′′y′)
算不下去了。。。。。
不过计算方式和曲率的导数一样。
5. C++与Python函数实现
计算曲率和曲率导数的c++函数如下:
// kappa = (dx * d2y - dy * d2x) / [(dx * dx + dy * dy)^(3/2)]
double CurveMath::ComputeCurvature(const double dx, const double d2x,
const double dy, const double d2y) {
const double a = dx * d2y - dy * d2x;
auto norm_square = dx * dx + dy * dy;
auto norm = std::sqrt(norm_square);
const double b = norm * norm_square;
return a / b;
}
double CurveMath::ComputeCurvatureDerivative(const double dx, const double d2x,
const double d3x, const double dy,
const double d2y,
const double d3y) {
const double a = dx * d2y - dy * d2x;
const double b = dx * d3y - dy * d3x;
const double c = dx * d2x + dy * d2y;
const double d = dx * dx + dy * dy;
return (b * d - 3.0 * a * c) / (d * d * d);
}
计算曲率和曲率导数的python函数如下:
def ComputeCurvature(dx, ddx, dy, ddy):
a = dx*ddy - dy*ddx
norm_square = dx*dx+dy*dy
norm = sqrt(norm_square)
b = norm*norm_square
return a/b
def ComputeCurvatureDerivative(dx, ddx, dddx, dy, ddy, dddy):
a = dx*ddy-dy*ddx
b = dx*dddy-dy*dddx
c = dx*ddx+dy*ddy
d = dx*dx+dy*dy
return (b*d-3.0*a*c)/(d*d*d)
def ComputeCurvature(dy, ddy):
a = ddy
norm_square = 1+dy*dy
norm = sqrt(norm_square)
b = norm*norm_square
return a/b
def ComputeCurvatureDerivative(dy, ddy, dddy):
a = ddy
b = dddy
c = dy*ddy
d = 1.0+dy*dy
return (b*d-3.0*a*c)/(d*d*d)
END
by windSeS
2020.9.6
最后
以上就是迅速唇彩最近收集整理的关于曲率、曲率(对弧长)的导数以及曲率导数(对弧长)的导数的计算的全部内容,更多相关曲率、曲率(对弧长)内容请搜索靠谱客的其他文章。








发表评论 取消回复