[NOIP2016]组合数问题

74 阅读 0 评论 49 点赞

我是靠谱客的博主热心黄蜂，最近开发中收集的这篇文章主要介绍[NOIP2016]组合数问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目描述：
题目链接： UOJ 263 http://uoj.ac/problem/263
题目背景: NOIP2016 提高组 Day2 T1
组合数表示的是从 n 个物品中选出 m 个物品的方案数。举个例子，从 (1,2,3) 三个物品中选择两个物品可以有 (1,2)，(1,3)，(2,3) 这三种选择方法。根据组合数的定义，我们可以给出计算组合数的一般公式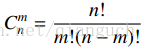：这里写图片描述其中 $n!=1×2×...×n$ 。
小葱想知道如果给定 n，m 和 k，对于所有的 0≤i≤n，0≤j≤min(i,m) 有多少对 (i,j) 满足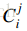是 k 的倍数。
输入格式:
第一行有两个整数 t，k，其中 t 代表该测试点总共有多少组测试数据，k 的意义见【问题描述】。
接下来 t 行每行两个整数 n，m，其中 n，m 的意义见【问题描述】。
输出格式:
输出 t 行，每行一个整数代表所有的 0≤i≤n，0≤j≤min(i,m) 中有多少对 (i,j) 满足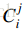这里写图片描述是 k 的倍数。
样例输入1：
1 2
3 3
样例输出1：
1
样例输入2：
2 5
4 5
6 7
样例输出2：
0
7
备注：
样例1说明：在所有可能的情况中，只有是 2 的倍数。
数据规模与约定：

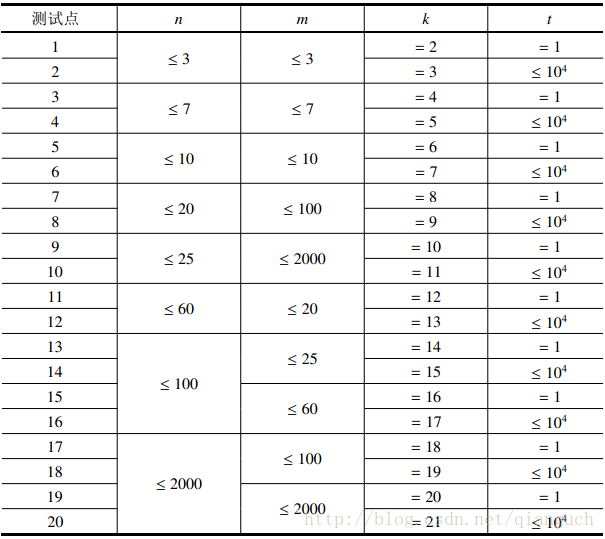
题目分析：
由组合数与杨辉三角的对应关系可知递推公式。令 $f[i][j]$ 代表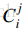这里写图片描述，得 $f[i][j]=f[i-1][j-1]+f[i-1][j]$ 。所以我们可以预处理出所有组合数，就得知是否是k的倍数。为避免爆int，更新时模k,这不影响判断。再开一个数组 $ans[i][j]$ ,记录对于i这一维到j时满足要求的数的个数。最后答案就是累加 $ans[1][min(1,j)]+ans[2][min(2,j)]+······+ans[i][min(i,j)]$ 。
附代码：

#include<iostream>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cstdio>
#include<ctime>
#include<queue>
#include<set>
#include<map>
#include<iomanip>
#include<cmath>
#include<cctype>
#include<algorithm>
using namespace std;

const int maxn=2010;
const int N=1e4+10;
int t,k,maxx,maxy,f[maxn][maxn],ans[maxn][maxn],n[N],m[N],sum;

void pre()
{
    f[0][0]=1;
    for(int i=1;i<=maxx;i++)
        for(int j=0;j<=i;j++)
        {
            f[i][j]=(f[i-1][j-1]+f[i-1][j])%k;
            if(f[i][j]==0) ans[i][j]++;
            ans[i][j]+=ans[i][j-1];
        }
}

int main()
{
    //freopen("lx.in","r",stdin);

    scanf("%d%d",&t,&k);
    for(int i=1;i<=t;i++)
    {
        scanf("%d%d",&n[i],&m[i]);
        if(n[i]>maxx) maxx=n[i];
        if(m[i]>maxy) maxy=m[i];
    }   
    pre();
    for(int i=1;i<=t;i++)
    {
        sum=0;
        for(int j=0;j<=n[i];j++)
        {
            int v=min(j,m[i]);
            sum+=ans[j][v];
        }   
        printf("%dn",sum);
    }

    return 0;
}