定义
在计数时,必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。 (没锤子用 )
讲解
最基础开始:设P1和P2是两个性质(例如“被6整除”)。我们想统计既不具有P1 也不具有P2性质的物体的个数。可以先排除掉具有P1的物体个数,然后再排除掉具有P2的物体个数,由于同时具有两种性质的物体被排除了两次,所以我们要把他们重新算回来,加上同时具有P1和P2的物体个数。
但是如果变成多维了呢,有3个性质或者4个性质呢,其实也是同样的道理

你会发现奇数是加,偶数是减,为什么是这样呢,看这个三个性质的图就行了
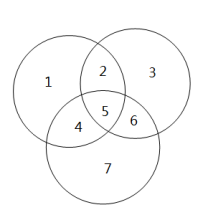
然后你就可以自己类比出来了

上面这个式子就是个补集
例题1

例题2

例题3
求出多重集合S={ a,a,a,b,b,b,b,c,c,c,c,c }的10组合数
1:首先假设这个多重集合a,b,c字母都无限多,那么numa+numb+numc=10求非负整数解
2:然后两边同时加3变成求numa‘+numb’+numc‘=13的正整数解,就是运用插空法在12个空里插2个隔板分为3个数,那么答案就是
s
u
m
=
C
12
2
=
66
sum=C_{12}^{2}=66
sum=C122=66
3:但是这个多重集合是有限制的。我们求出所有不满足的情况然后相减。性质1: 10-组合中有 大于3个a。性质2: 10-组合中有 大于4个b 。
性质3: 10-组合中有 大于5个c .
4:
∣
A
1
∣
:
|A_1|:
∣A1∣:a至少出现4次剩下随便选有
C
8
2
=
28
C_{8}^{2}=28
C82=28,
∣
A
2
∣
:
|A_2|:
∣A2∣:b出现5次剩下随便选有
C
7
2
=
21
C_{7}^{2}=21
C72=21,
∣
A
3
∣
:
|A_3|:
∣A3∣:c出现6次剩下随便选的情况有
C
6
2
=
15
C_{6}^{2}=15
C62=15
5:
∣
A
1
∣
∩
∣
A
2
∣
=
C
3
2
=
3
∣
A
1
∣
∩
∣
A
3
∣
=
C
2
2
=
1
∣
A
1
∣
∩
∣
A
3
∣
=
0
|A_1|∩|A_2|=C_{3}^{2}=3 |A_1|∩|A_3|=C_{2}^{2}=1 |A_1|∩|A_3|=0
∣A1∣∩∣A2∣=C32=3∣A1∣∩∣A3∣=C22=1∣A1∣∩∣A3∣=0
6:
∣
A
1
∣
∩
∣
A
2
∣
∩
∣
A
3
∣
=
0
|A_1|∩|A_2|∩|A_3|=0
∣A1∣∩∣A2∣∩∣A3∣=0:
7:
a
n
s
=
s
u
m
−
∣
A
1
∣
−
∣
A
2
∣
−
∣
A
3
∣
+
∣
A
1
∣
∩
∣
A
2
∣
+
∣
A
1
∣
∩
∣
A
3
∣
+
∣
A
2
∣
∩
∣
A
3
∣
−
∣
A
1
∣
∩
∣
A
2
∣
∩
∣
A
3
∣
=
6
ans=sum-|A_1|-|A_2|-|A_3|+|A_1|∩|A_2|+|A_1|∩|A_3|+|A_2|∩|A_3|-|A_1|∩|A_2|∩|A_3|=6
ans=sum−∣A1∣−∣A2∣−∣A3∣+∣A1∣∩∣A2∣+∣A1∣∩∣A3∣+∣A2∣∩∣A3∣−∣A1∣∩∣A2∣∩∣A3∣=6即
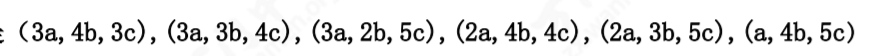
模板题
代码
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<cstdio>
#include<vector>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_map>
#define fi first
#define se second
#define debug printf(" I am heren");
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
const ll INF=0x3f3f3f3f3f3f3f3f;
const int maxn=1e6+5,inf=0x3f3f3f3f,mod=1e9+7;
const double eps=1e-10;
ll a,b,n,fac[20],sum1,sum2,cnt,tot;
int cal(int x){
int cnt=0;
while(x){
cnt+=(x%2);
x=x/2;
}
return cnt;
}
ll gcd(ll a,ll b){
return b==0?a:gcd(b,a%b);
}
signed main(){
int _;scanf("%d",&_);
while(_--){
sum1=sum2=cnt=0;
scanf("%lld%lld%lld",&a,&b,&n);
for(ll i=2;i*i<=n;i++){
if(n%i==0){
fac[++cnt]=i;
}
while(n%i==0){
n=n/i;
}
}
if(n>1){
fac[++cnt]=n;
}
for(int sta=0;sta<(1<<cnt);sta++){
int num=cal(sta);
if(num==0) continue;
ll lcm=1;
for(int i=1;i<=cnt;i++){
if(sta&(1<<(i-1))){
lcm=lcm*fac[i]/gcd(lcm,fac[i]);
}
}
if(num%2){
sum1+=b/lcm;
sum2+=(a-1)/lcm;
}else{
sum1-=b/lcm;
sum2-=(a-1)/lcm;
}
}
printf("Case #%lld: %lldn",++tot,b-a+1-(sum1-sum2));
}
return 0;
}
好像这个题目还能用莫比乌斯反演优化,然而我先把基础的学了吧qwq
最后
以上就是独特板凳最近收集整理的关于容斥定理入门的全部内容,更多相关容斥定理入门内容请搜索靠谱客的其他文章。








发表评论 取消回复