FFT补零不能增加物理分辨率，只能增加计算分辨率。若要增加物理分辨率，唯一的方法是增加信号的有效长度。

60 阅读 0 评论 40 点赞

我是靠谱客的博主喜悦毛巾，最近开发中收集的这篇文章主要介绍FFT补零不能增加物理分辨率，只能增加计算分辨率。若要增加物理分辨率，唯一的方法是增加信号的有效长度。，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

分辨率有两种含义：一种是指在谱分析中将信号x（n）中两个靠得很近的谱峰仍然能保持分辨的能力；另一种是指在使用DFT时，在频率轴上的所能得到的最小频率间隔。通常把第一种分辨率称为物理分辨率，而把第二种分辨率称为计算分辨率。

一、物理分辨率：

设信号x（t）的最高频率分量为fc，要求信号x（t）在离散后谱分析中两个频率间隔为fδ的谱峰仍能分辨。为了满足采样定理，可以导出采样频率fs：

fs≥2fc

即采样频率应大于信号最高频率的两倍。当信号取有限长T秒部分后得xT（t），又经过采样，信号成为离散值xM（nTs)，简写为x（n)，其中Ts是采样周期（Ts=1/fs)，M是x（n)的样点数，有

M=T/Ts

从有限长离散傅里叶变换可知，离散频谱的频率间隔为△f=fs/N=1/（Ts*N）。为了满足谱分析中两个频率间隔为fδ的谱峰仍能分辨，即要求△f≤fδ，可得到

fδ≥△f=1/（MTs）=fs/M

这样可以进一步确定M或者T的长度：

M≥fs/fδ=1/(fδTs) 或 MTs=T≥1/fδ

将Tmin=MTs=1/fδ

定义为最小记录长度，即当要求在谱分析中两个频率间隔为fδ的谱峰仍能分辨，则信号的最小长度为Tmin。Tmn只与fδ要求有关，故称式△f=fs/M为物理分辨率，其中fs是采样频率，M是数据的实际样点数。但以上的推导都是在矩形窗的条件下得到的，若加其他窗函数，则变为

M≥(fs/fδ)K

式中：K为窗函数的主瓣宽度与矩形窗的主瓣宽度之比。

二、计算分辨率：

离散频谱的频率间隔为△f=fs/N=1/（TsN)，其中N可以不等于M，且常对数据进行补零。例如数据长M，且M不为2^k，在进行FFT时常把数据补零使数据长度为N=2^k（k为正整数），以便于使用FFT的运算。这时△f只是谱分析中谱线之间的频率间隔，它与fs和N有关，即与具体计算有关，故称为计算分辨率。

案例、信号由3个正弦信号组成，频率分别为1Hz、2.5Hz、3Hz，采样频率fs为10Hz，信号长度为N=10。我们通过补零观察是否能分辨2.5Hz与3Hz。
已知要能分辨2.5Hz与3Hz,则N至少长为20。当N=40时，能很清楚地看出2.5Hz与3Hz分别有一个峰值。本程序分为两部分，先以N=10进行FFT，再以N=40（等于10个数据后补了30个零值）进行FFT，观察它们的频谱。程序如下：

clear all; clc; close all;

M=10; fs=10;                                    % 设置数据长度M和采样频率fs
f1=1; f2=2.5; f3=3;                             % 设置3个正弦信号的频率
t=(0:M-1)/fs;                                   % 设置时间序列
x=cos(2*pi*f1*t)+cos(2*pi*f2*t)+cos(2*pi*f3*t); % 计算出信号波形

X1=fft(x);                                      % FFT变换
freq1=(0:5)*fs/10;                              % 计算3个信号在频域的频率刻度
X2=fft(x,40);                                   % FFT变换
freq2=(0:20)*fs/40;                             % 计算3个信号在频域的频率刻度
% 作图
plot(freq1,abs(X1(1:6)),'k-.',freq2,abs(X2(1:21)),'k');
title('补零后DFT变换');
xlabel('频率/Hz'); ylabel('幅值');
legend('FFT变换长为10','FFT变换长为40')
set(gcf,'color','w');

运行结果如下：

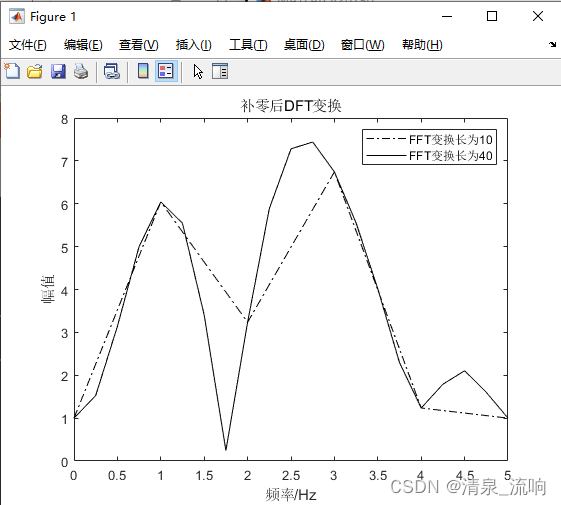
图中所示虚线是FFT变换长度为10。已知N=10是不能分辨2.5Hz与3Hz的频率分量的，但能分辨1Hz与2.5Hz分量，所以图中有2个虚线的峰值。但当对数据补零，使FFT长为40时，计算结果在图中用实线表示，可以看出还是2个峰值，与FFT长为10的结果相类似。在以前的案例中，当N=40时，可清楚分辨2.5Hz与3Hz,现在通过补零的方法一样取FFT长为40，但结果完全不同。说明补零不能增加物理分辨率，只能增加计算分辨率。要增加物理分辨率，唯一的方法是增加信号的有效长度。

涉及到的相关文章链接：

https://blog.csdn.net/qq_42233059/article/details/126459560?spm=1001.2014.3001.5502

参考文献：MATLAB数字信号处理85个实用案例精讲——入门到进阶；宋知用（编著）