1. 首页
  2. 文章中心
  3. Other

快速傅里叶变换(FFT)中为什么要“补零”？

92 阅读 0 评论
我是靠谱客的博主 直率万宝路，最近开发中收集的这篇文章主要介绍快速傅里叶变换(FFT)中为什么要“补零”？，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

为了大家能够复现各个图中的结果，我附上了所有我编写的MATLAB代码。

创作不易，未经允许，禁止转载。

另外，说明一下，用MATLAB做FFT并不要求数据点个数必须为以2为基数的整数次方。之所以很多资料上说控制数据点数为以2为基数的整数次方，是因为这样就能采用以2为基的FFT算法，提升运算性能。

如果数据点数不是以2为基数的整数次方，处理方法有两种，一种是在原始数据开头或末尾补零，即将数据补到以2为基数的整数次方，这是“补零”的一个用处；第二种是采用以任意数为基数的FFT算法。

快速傅里叶变换 FFT

 

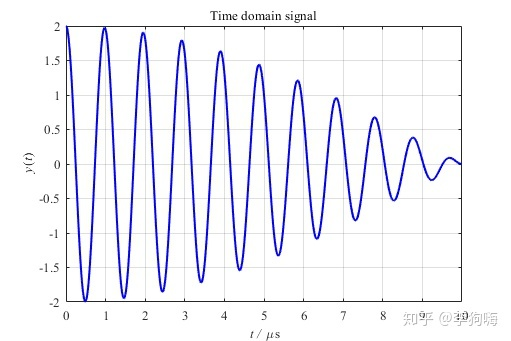
图1. 1000个数据点

如果，直接对这1000个数据点其做快速傅里叶变换，将得到频谱图：

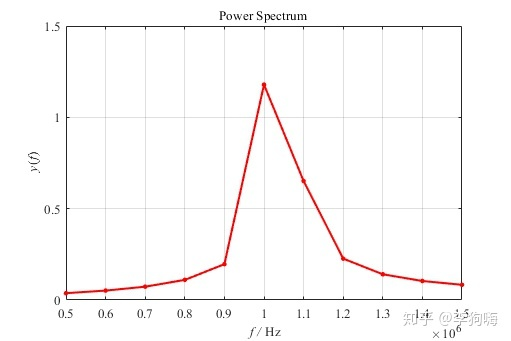
图2. 1000个数据点做FFT的频谱

可以发现，频谱点稀疏，在1MHz附近根本无法将1 MHz 和1.05 MHz 的两个频率分开。

clear;clc
close all
%% FFT
Fs = 100e6;		    % 采样频率 Hz
T = 1/Fs;		    % 采样周期 s
L0 = 1000;                  % 信号长度
L = 1000;                   % 数据长度
t0 = (0:L0-1)*T;            % 信号时间序列
x = cos(2*pi*1e6*t0) + cos(2*pi*1.05e6*t0); % 信号函数
t = (0:L-1)*T;              % 数据时间序列
%% Plot
figure(1)
plot(t*1e6,x,'b-','linewidth',1.5)
title ('fontsize{10}fontname{Times New Roman}Time domain signal')
xlabel('fontsize{10}fontname{Times New Roman}it t /rm mus')
ylabel('fontsize{10}fontname{Times New Roman}it yrm(ittrm)')
grid on;
axis([0 10 -2 2])
set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')
set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')
%% FFT
Y = fft(x);                   % 快速傅里叶变换
% 计算双侧频谱 P2。然后基于 P2 和偶数信号长度 L 计算单侧频谱 P1。
P2 = abs(Y/L0);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;% Rfft
figure(2)
plot(f, P1,'r-','Marker','.','markersize',10,'linewidth',1.5)
axis([0.5e6 1.5e6 0 1.5])
title('fontsize{10}fontname{Times New Roman}Power Spectrum')
xlabel('fontsize{10}fontname{Times New Roman}it f /rm Hz')
ylabel('fontsize{10}fontname{Times New Roman}it yrm(itfrm)')
grid on;
set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')
set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')

频率分辨率

发现频率成分无法被区分开来，第一反应应该就是：频率分辨率不够。那么，如何提高频率分辨率呢？首先要清楚，这里存在两种类型的频率分辨率。

补零

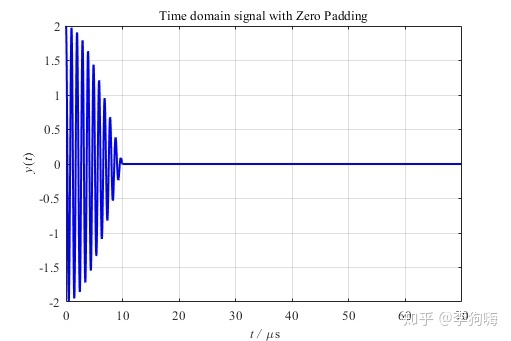
图3. 7000个补零后数据点

此时对其做快速傅里叶变换，结果如下：

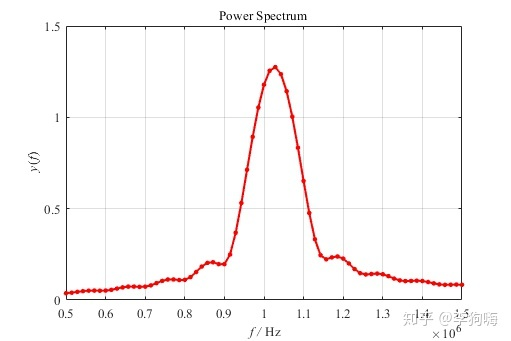
图4. 7000个补零后数据点做FFT的频谱

clear;clc
close all
%% FFT
Fs = 100e6;		    % 采样频率 Hz
T = 1/Fs;		    % 采样周期 s
L0 = 1000;                  % 信号长度
L = 7000;                   % 数据长度
t0 = (0:L0-1)*T;            % 信号时间序列
x = cos(2*pi*1e6*t0) + cos(2*pi*1.05e6*t0); % 信号函数
t = (0:L-1)*T;              % 数据时间序列
y = zeros(1,L);
y(1:L0) = x;
%% Plot
figure(1)
plot(t*1e6,y,'b-','linewidth',1.5)
title('fontsize{10}fontname{Times New Roman}Time domain signal with Zero Padding')
xlabel('fontsize{10}fontname{Times New Roman}it t /rm mus')
ylabel('fontsize{10}fontname{Times New Roman}it yrm(ittrm)')
grid on;
axis([0 70 -2 2])
set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')
set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')
%% FFT
Y = fft(y);                   % 快速傅里叶变换
% 计算双侧频谱 P2。然后基于 P2 和偶数信号长度 L 计算单侧频谱 P1。
P2 = abs(Y/L0);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;% Rfft
figure(2)
plot(f, P1,'r-','Marker','.','markersize',10,'linewidth',1.5)
axis([0.5e6 1.5e6 0 1.5])
title('fontsize{10}fontname{Times New Roman}Power Spectrum')
xlabel('fontsize{10}fontname{Times New Roman}it f /rm Hz')
ylabel('fontsize{10}fontname{Times New Roman}it yrm(itfrm)')
grid on;
set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')
set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')

频谱泄漏

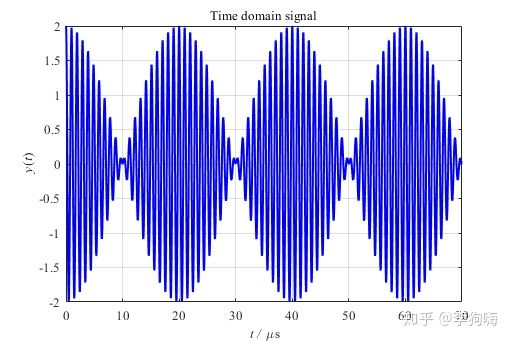
图5. 7000个数据点

对其做快速傅里叶变换，结果如下：

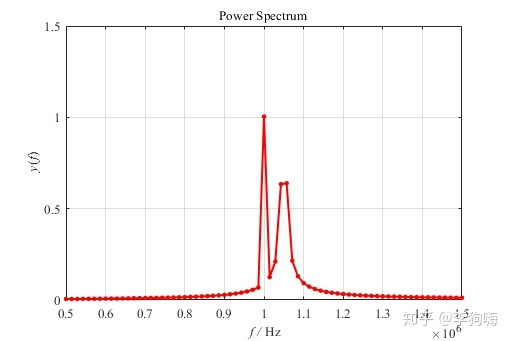
图6. 7000个数据点做FFT的频谱

clear;clc
close all
%% FFT
Fs = 100e6;		    % 采样频率 Hz
T = 1/Fs;		    % 采样周期 s
L0 = 7000;                  % 信号长度
L = 7000;                   % 数据长度
t0 = (0:L0-1)*T;            % 信号时间序列
x = cos(2*pi*1e6*t0) + cos(2*pi*1.05e6*t0); % 信号函数
t = (0:L-1)*T;              % 数据时间序列
%% Plot
figure(1)
plot(t*1e6,x,'b-','linewidth',1.5)
title('fontsize{10}fontname{Times New Roman}Time domain signal')
xlabel('fontsize{10}fontname{Times New Roman}it t /rm mus')
ylabel('fontsize{10}fontname{Times New Roman}it yrm(ittrm)')
grid on;
axis([0 70 -2 2])
set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')
set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')
%% FFT
Y = fft(x);                   % 快速傅里叶变换
% 计算双侧频谱 P2。然后基于 P2 和偶数信号长度 L 计算单侧频谱 P1。
P2 = abs(Y/L0);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs/2*linspace(0,1,L/2+1);% Rfft
figure(2)
plot(f, P1,'r-','Marker','.','markersize',10,'linewidth',1.5)
axis([0.5e6 1.5e6 0 1.5])
title('fontsize{10}fontname{Times New Roman}Power Spectrum')
xlabel('fontsize{10}fontname{Times New Roman}it f /rm Hz')
ylabel('fontsize{10}fontname{Times New Roman}it yrm(itfrm)')
grid on;
set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')
set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')

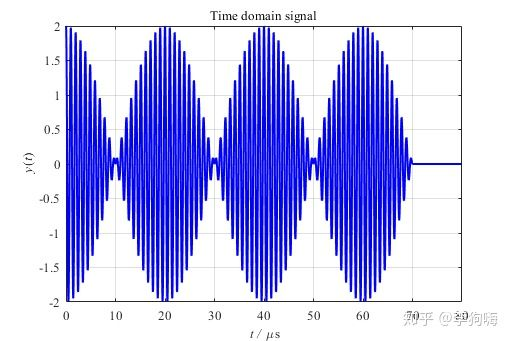
图7. 8000个补零后数据点

对其做快速傅里叶变换，结果如下：

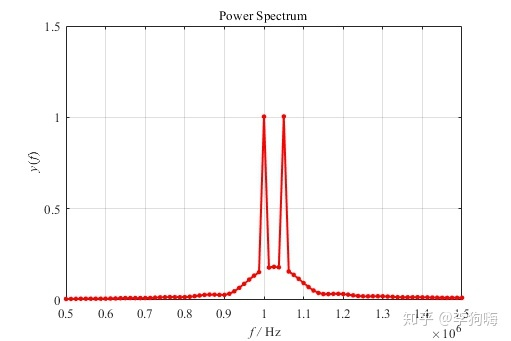
图8. 8000个补零后数据点做FFT的频谱

clear;clc
close all
%% FFT
Fs = 100e6;	            % 采样频率 Hz
T = 1/Fs;		    % 采样周期 s
L0 = 7000;                  % 信号长度
L = 8000;                   % 数据长度
t0 = (0:L0-1)*T;            % 信号时间序列
x = cos(2*pi*1e6*t0) + cos(2*pi*1.05e6*t0); % 信号函数
t = (0:L-1)*T;              % 数据时间序列
y = zeros(1,L);
y(1:L0) = x;
%% Plot
figure(1)
plot(t*1e6,y,'b-','linewidth',1.5)
title('fontsize{10}fontname{Times New Roman}Time domain signal')
xlabel('fontsize{10}fontname{Times New Roman}it t /rm mus')
ylabel('fontsize{10}fontname{Times New Roman}it yrm(ittrm)')
grid on;
axis([0 80 -2 2])
set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')
set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')
%% FFT
Y = fft(y);                   % 快速傅里叶变换
% 计算双侧频谱 P2。然后基于 P2 和偶数信号长度 L 计算单侧频谱 P1。
P2 = abs(Y/L0);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs/2*linspace(0,1,L/2+1);% Rfft
figure(2)
plot(f, P1,'r-','Marker','.','markersize',10,'linewidth',1.5)
axis([0.5e6 1.5e6 0 1.5])
title('fontsize{10}fontname{Times New Roman}Power Spectrum')
xlabel('fontsize{10}fontname{Times New Roman}it f /rm Hz')
ylabel('fontsize{10}fontname{Times New Roman}it yrm(itfrm)')
grid on;
set(gca,'FontSize', 10 ,'FontName', 'Times New Roman')
set(gcf,'unit','centimeters','position',[15 10 13.53 9.03],'color','white')

图8 中会有一些旁瓣出现，这是因为补零影响了原始信号，如果，直接采8000个点作为原始数据，即将程序中的L0改为8000，那么有：

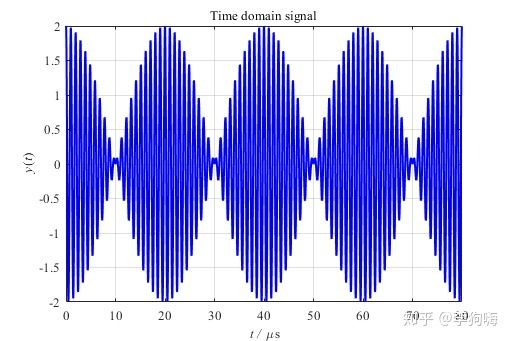
图9. 8000个数据点

并对其做FFT，结果如下

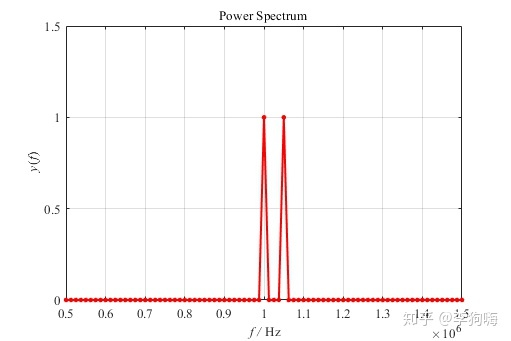
图10. 8000个数据点做FFT的频谱

这样就不存在补零带来的误差了。

参考

  1. ^Zero Padding http://www.bitweenie.com/listings/fft-zero-padding/
  2. ^Zero Padding Theorem https://ccrma.stanford.edu/~jos/dft/Zero_Padding_Theorem_Spectral.html

最后

以上就是直率万宝路为你收集整理的快速傅里叶变换(FFT)中为什么要“补零”？的全部内容，希望文章能够帮你解决快速傅里叶变换(FFT)中为什么要“补零”？所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(61)

相关文章

N个点FFT变换中的频率分辨率以及与实际频率的关系
N个点FFT变换中的频率分辨率以及与实际频率的关系
关于FFT的一些
关于FFT的一些
FFT补零不能增加物理分辨率，只能增加计算分辨率。若要增加物理分辨率，唯一的方法是增加信号的有效长度。
FFT补零不能增加物理分辨率，只能增加计算分辨率。若要增加物理分辨率，唯一的方法是增加信号的有效长度。
补零与离散傅里叶变换的分辨率
补零与离散傅里叶变换的分辨率
快速傅里叶变换(FFT)中为什么要“补零”？
快速傅里叶变换(FFT)中为什么要“补零”？
一篇关于FFT补零的分析文章
一篇关于FFT补零的分析文章
频谱细化-----CZT算法介绍及MATLAB实现
频谱细化-----CZT算法介绍及MATLAB实现
常见算法
常见算法

评论列表共有 0 条评论

立即
投稿
返回
顶部