fft 估计载波频率程序_FFT和示波器实用指南——深圳零式未来仪器科技

通用测试仪器

本文讨论了一些重要的FFT特性，解释了如何利用这些特性设置FFT以实现高效的分析。

快速傅里叶变换(FFT)是20世纪70年代微处理器进入商业设计时首次出现的。从昂贵的实验室型号到最便宜的业余型号，现在几乎每一台示波器都能提供FFT分析功能。FFT是一种功能强大的工具，高效使用FFT要求人们对FFT有一定的研究。本文将介绍如何设置FFT和高效使用FFT，FFT的技术原理这里不再赘述。

FFT是一种能够缩短离散傅里叶变换(DFT)计算时间的算法，也是一种用于在频域(幅度和相位与频率的关系)中查看所采集的时域(幅度与时间)数据的分析工具。FFT给数字示波器增加了频谱分析功能。

观察图1中的上半部分曲线，你看到的是一个经过幅度调制的载波，它使用梯形脉冲作为调制函数。在看图1中的这个时域图时，如果让你告诉我信号的带宽，你可能一时答不上来。但如果你对这个信号进行FFT处理，就能得到另外一个视角。这个信号有一个线性扫描的频率，带宽用光标标记出来了，是4.7MHz。这正是示波器中增加FFT功能的原理，它是从另外一个角度来看同样的数据。

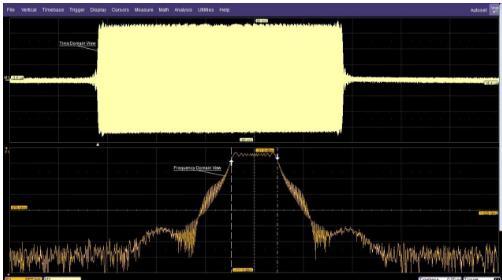
示波器中增加FFT功能的原理

FFT和示波器：实用指南

图1：上面的时域图显示了脉冲调制的射频载波，下方的频域图显示了在997MHz和1002MHz之间均匀分布的载频

FFT频带宽度和分辨率带宽

在最早的电路课程中，你应该学过周期信号的频率(频域)是周期(时域)的倒数。同样，这个关系贯穿在整个FFT设置过程中。

设置FFT最好从选择分辨率带宽(RBW)开始，因为它与单参调整有关。RBW (Δf)是显示FFT频率轴的增量步距。在时域中，采样周期决定了样本之间的时间间隔。而在频域中，RBW是频谱图中相邻“单元”之间的频率差值。RBW是时域记录长度(也称为采集时间)的倒数，如图2所示。你可以用示波器的水平刻度或时间/格参数设置来控制RBW。图1中的采集时长是20μs，频谱图中的RBW是它的倒数，即50kHz。

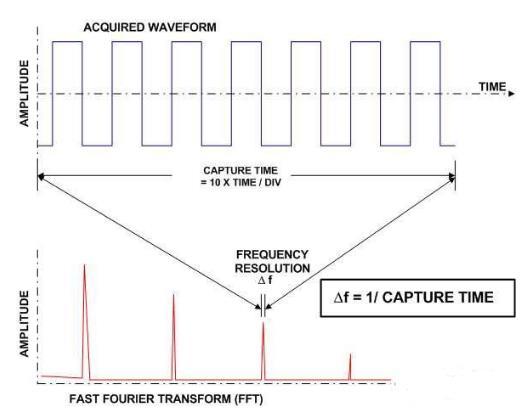
FFT频带宽度和分辨率带宽

FFT和示波器：实用指南

设置FFT的下一步是确定频域图的宽度——FFT中最高频率和最低频率之差。注意，FFT通常从0 Hz开始，一直到整个频带宽度。这与射频频谱分析仪有很大的区别，马上我会讲到。

FFT的频带宽度是示波器有效采样率的一半(图3)。时域中的最短时间增量——采样周期——决定了频域中的最大分量。同样，频域中的最小增量是时间记录中最长持续时间的函数。这符合时域和频域之间的倒数关系。

FFT和示波器：实用指南

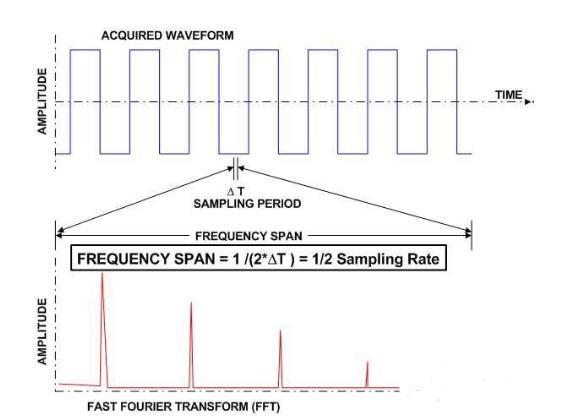
设置FFT的下一步是确定频域图的宽度——FFT中最高频率和最低频率之差

为了在频域中取得更高的分辨率，必须增加采集的数据量，方法是增加时间/格设置值。这与在示波器的时域图中增加时间分辨率的做法刚好是相反的。

从实用的角度看，时域记录长度是由示波器的时间/格参数值控制的。一旦你选择了时间/格参数值来达到想要的分辨率带宽，那么控制采样率达到所需频带宽度的唯一方法是修改示波器的采集内存长度。现在事情似乎复杂起来了，确实是这样。

最近，大多数高端示波器制造商都修改了FFT用户界面，使它更类似于标准的射频频谱分析仪，设置中心频率和频带宽度时将分辨率带宽作为一个参数。虽然这类界面使得FFT使用起来更容易，但确实隐藏了FFT的基本功能，导致必须接受示波器设置的时间/格、采样率和内存长度组合。根据这部分讨论的一些规则，你可以手工设置FFT，并在设置中获得更多的自由度。

垂直缩放

根据示波器的不同，FFT也许可以选择垂直刻度，也许只能是固定的单一垂直格式。最常见的垂直格式是功率谱，它以功率为单位显示垂直幅度，常用相对于1毫瓦的分贝表示(dBm)，并在对数垂直刻度上显示。这种选择也是射频频谱分析仪功能的保留。实验室级别的示波器可以提供更多的数据，包括功率谱密度(PSD)、线性幅度、平方幅度、相位或实数/虚数分量。

PSD是归一化为FFT分辨率带宽的功率谱值。它的测量单位是dBm/Hz，代表单位带宽上的功率。PSD在测量宽带现象(如噪声)时非常有用。幅度格式显示示波器测量的线性单位的频谱幅度，如伏特(V)或安培(A)。

幅度平方显示顾名思义是将频谱幅值显示为幅度的平方值，单位可以是V²、A²等等，并且在归一化为仪器输入阻抗(通常是50Ω)时为功率测量提供线性缩放。归一化是利用示波器的再缩放函数实现的，它允许乘以一个常数。对于50Ω来说，幅度平方谱乘以0.02(即1/50)，即对于50Ω输入阻抗而言将单位改为瓦(V²/50)。

从数学的角度来看FFT频谱是一个复杂函数，幅值的显示只是全貌的一半。FFT输出由实数和虚数部分组成，一些示波器可以同时显示这两部分。作为实数分量和虚数分量的替代，许多示波器显示FFT相位和幅值。这两个成对的输出格式(实数/虚数和幅值/相位)构成了完整的FFT。计算反向FFT时要求实数/虚数分量，在机械应用(如振动测量)中它们更常用，幅度/相位格式在电气测量中也常见到。图4显示了一个方波的功率谱幅值/相位和实数/虚数分量的例子。

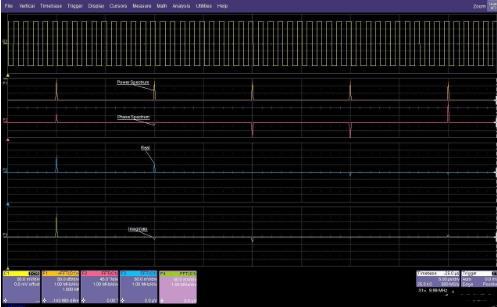
一个方波的FFT的功率谱幅值、相位、实数和虚数分量

FFT和示波器：实用指南

图4：一个方波的FFT的功率谱幅值、相位、实数和虚数分量

相位谱使用垂直单位度，实数和虚数格式使用与源通道相同的垂直单位，在本例中是mV。对于类似这种方波的周期性波形，相位、实数和虚数格式只在基频和谐波频率点有有效值。

加权函数

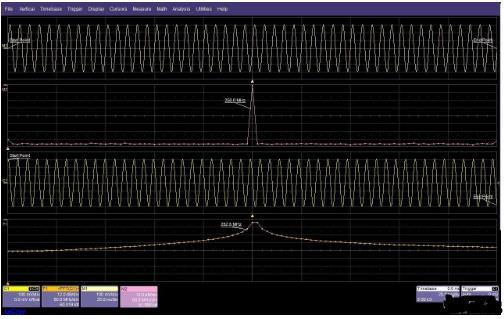
示波器中实现的FFT具有有限的记录长度，这将在频谱显示中引起问题，原因是获取的波形的起点和终点的连续性问题。图5显示了起点和终点是如何影响频谱形状的。

FFT和示波器：实用指南

图5的上面两个波形中，所采集的信号频率是采样率的因数，获取的波形中存在整数的周期性，起点和终点处于相同的幅度，结果生成的频谱非常窄。在下面两个波形中，所采集的信号的频率不是采样速率的因数，起点和终点位于不同的电平。

这将导致时间记录的不连续性。生成的频谱变得更宽，峰值电平更低，原因是频谱扩展(也称为泄漏)，即采集信号的能量被扩展到了相邻频率单元。更低的、与频率有关的峰值响应被称为“尖桩篱栅”效率或扇形损耗。加权(开窗)有助于最大限度地减小这些效应。

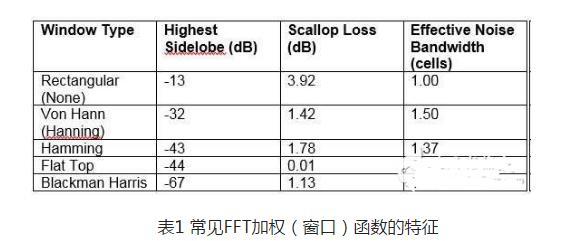
加权是将获取的波形乘以一个窗口函数，通过调制将端点变为零。窗口函数的形状决定了频谱响应，包括频谱线的形状和任何边带的幅度。常用加权函数的特征如表1所示。

FFT和示波器：实用指南

表1 常见FFT加权(窗口)函数的特征

这张表对每个窗口最大限度减小旁瓣和扇形损耗的能力进行了总结。图6显示了在相同输入信号条件下窗口函数对谱线的影响。

FFT和示波器：实用指南

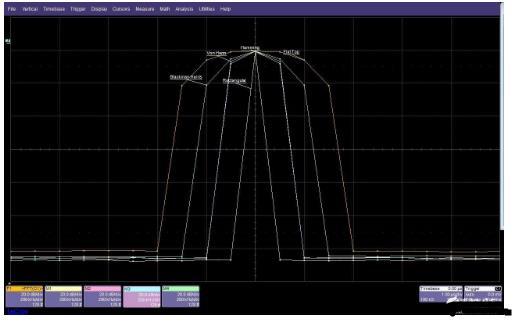
加权函数对频谱响应的影响

图6：这个屏幕图像比较了在相同输入信号条件下不同加权函数对频谱响应的影响

谱线变宽可以减小扇形损耗，这是有意义的，因为相邻单元中的信号会在更高幅度点重合，以获得更宽的响应，并最大限度地减小扇形损耗。

窗口函数的选择取决于具体需求。如果你要测量比采集窗口小的瞬变，那么不要使用窗口函数，因为频谱峰值的幅度将根据采集窗口中的瞬态位置发生改变。在这种情况下，矩形窗口(无加权)是最好的选择。越窄的窗口响应可以提供越好的频率分辨率和更宽的响应——Blackman Harris或平顶窗口——产生更为精确的幅度测量结果。如果你要两者兼顾，一个好的折衷方案是Von Hann或Hamming窗口。

频域平均

平均操作可以用来改善采集信号的信噪比，并且通常要求多次采集。平均可以在时域完成，也可以在频域完成。与触发事件不同步的信号，比如噪声，将与平均次数呈正比衰减。图7是频域平均的一个例子。

FFT和示波器：实用指南

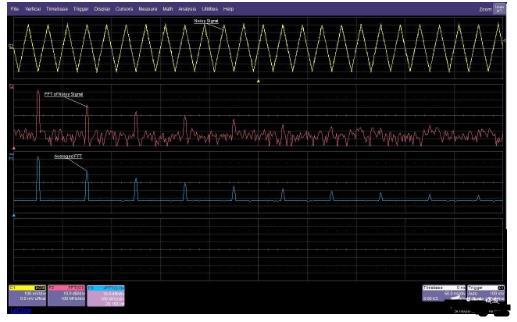
频域平均可以改善信噪比，并提供更大的动态测量范围。有噪信号FFT在经过许多次采集的平均后可以消除噪声

图7：频域平均可以改善信噪比，并提供更大的动态测量范围。有噪信号FFT在经过许多次采集的平均后可以消除噪声，从而看到更低电平的谐波

频域中的平均是将多次采集的每个频率单元的内容累加起来然后除以采集次数实现的。那些与采集不同步的信号将被平均为零，而同步信号则连续累加。在图7中，有噪信号的FFT包含频谱被扩展的噪声分量，这些噪声隐藏了低电平的谐波。平均有助于提高信噪比，减少噪声，使得谐波分量可见。以同样的方式，那些与采集不同步的信号幅度也将降低。

设置实例

考虑需要在一个4GHz带宽的示波器上设置FFT，其频带宽度是10MHz，中心频率是2.48GHz，分辨率带宽为10kHz，用于分析一个连续的周期性信号。根据上述讨论，只需简单地设置示波器的时间/格参数就能完成分辨率带宽的设置。10kHz的分辨率带宽要求采集或捕获时间为100μs，或者时间/格参数设为10μs /格。还应设置示波器的垂直灵敏度(电压/格)，以便信号占据至少90%的输入范围，尽量提高其动态范围。

FFT的频带宽度由采样率控制。由于这个宽度必须包含2.48GHz信号频率，因此必须大于这个频率的两倍。5GHz或更高的频率应该没问题。示波器的最大采样率是20 GS/s。利用示波器的时基设置来调整采集内存长度，可以获得想要的采样率。在本例使用的示波器中，将内存长度设为1MS，可以实现10GS/s的采样率和100μs的采集时间。详细的FFT设置见图8。

FFT和示波器：实用指南

图8：适合本例使用的主要FFT参数设置

数学函数F1的FFT栏包含一些主要的FFT设置，并被设置为显示功率谱。由于信号被显示为连续的，因此加权函数类型可以选择Von Hann窗口，它可以在频率分辨率和幅度平坦度之间提供很好的折衷。

FFT栏显示分辨率带宽(Δf)为10kHz，宽度为5GHz。缩放栏可以让你将中心频率设为2.48GHz，水平刻度设为1MHz/格，如图8中的F1轨迹所示。

小结

零式未来仪器代理本文讨论了一些重要的FFT特性，解释了如何利用这些特性设置FFT以实现高效的分析。等下次你要在示波器中使用FFT时希望能助你一臂之力。