连续信号频域分析：功率信号的频谱与能量信号频谱密度

频域分析：

周期信号and非周期信号幅度谱都是偶函数。

一、功率(周期)信号的频谱

        认为周期信号为功率信号、非周期信号为能量 信号

        1.1周期信号的虚指数/三角傅里叶级数：

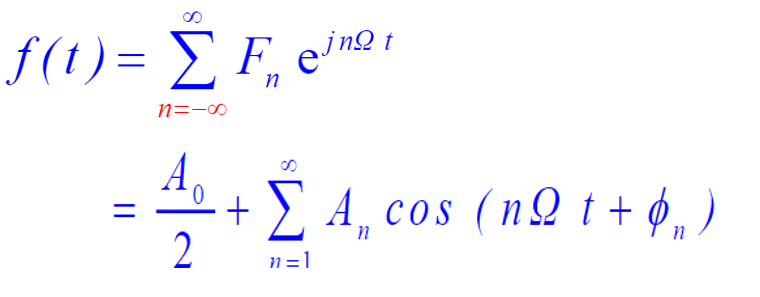
        其中， 

        1.2 意义：从频域上看，周期信号是由其所有频率分量叠加而成，并且这些频域分量都是周期信号频率的整数倍，傅里叶级数的作用就是算出这些不同的频率分量的幅度和相位。

        从时域上看，周期函数是有其不同频率分量对应的正弦函数叠加而成，因为单个频率分量对应的时域信号为正弦函数。

        1.3所以，周期信号的频域分析就是分析频谱：幅度谱和相位谱。两种完备集对应的频谱关系如下：

        (1)三角函数：频谱都是单边谱

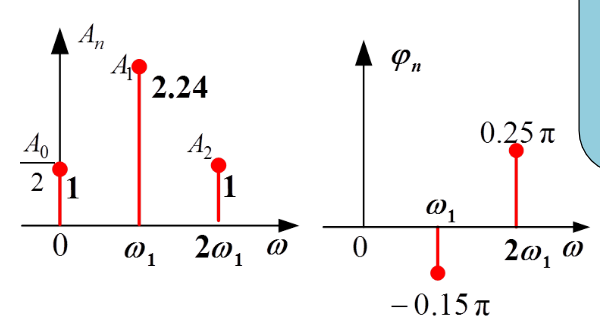
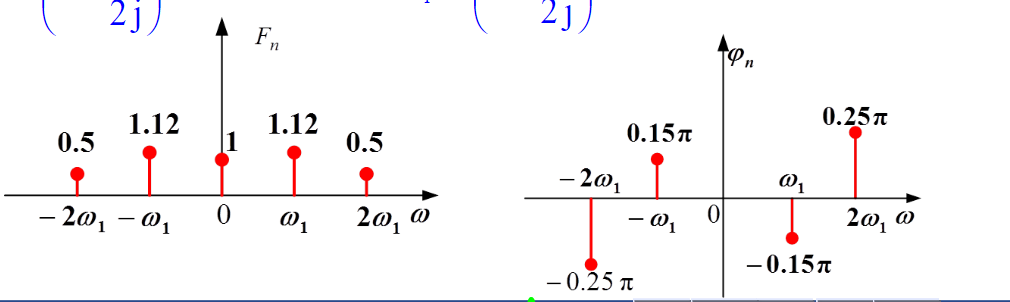
        (2)虚指数 ：频谱都是双边谱

        幅度谱：关于纵轴对称是偶函数，正频率和负频率的幅度大小只有单边谱An的一半，直流分量单边谱双边谱一致；

        相位谱：奇函数，相位大小与单边谱相位谱一样，只不过多了对称的负频率部分。

二、功率(周期)信号的功率谱密度

        周期信号由于能量无限，所以没有能量谱，只有功率谱

三.能量(非周期)信号频谱密度 

        非周期信号的频域用傅里叶变换分析：

        2.1为什么是频谱密度，不是频谱？

        因为非周期信号之所以利用FT是因为其傅里叶级数都趋于0(非周期信号=周期趋于无穷的周期信号，所以其复傅里叶系数Fn=0，所以傅里叶级数无法反映非周期信号不同频率分量间的大小关系)，所以采用傅里叶变换，放大不同频率分量间的大小关系，而且其频谱是连续函数，只可表示其密度。

        2.2

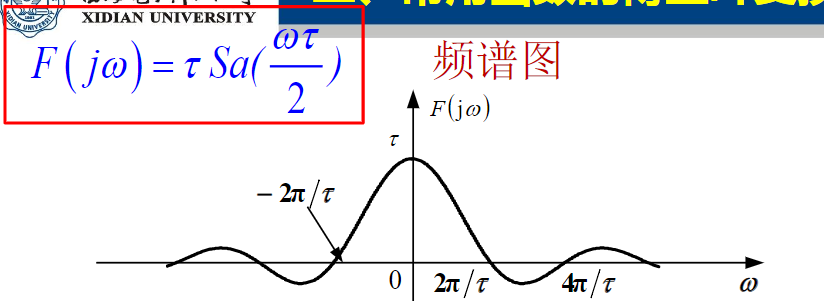
        2.3 特点：周期信号和非周期信号频谱都是正频率与负频率模偶对称，相位奇对称。

        2.4FT

        引入冲激函数后，周期信号的频谱可以用FT分析，各谐波频率分量处幅度为∞，用冲激函数表示

四.能量(非周期)能量谱密度

        即FT的平方

五.自相关函数

        功率信号的自相关函数与功率谱是一对傅里叶变换对，可以通过求自相关函数的FT求功率谱密度。

        能量信号的自相关函数与能量谱是一对傅里叶变换对，可以通过求自相关函数的FT求能量密度。

最后

以上就是精明秀发为你收集整理的连续信号频域分析：功率信号的频谱与能量信号频谱密度的全部内容，希望文章能够帮你解决连续信号频域分析：功率信号的频谱与能量信号频谱密度所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。