题意

问N有多少个排列满足，对于i∈[1,n]，有$|a_i-i|̸=K$
答案对924844033取模

题解

如果我们算出至少i个位置不满足这个条件的方案数（令之为f(i)），那我们就可以通过容斥来实现这道题
那么f(i)怎么求呢
我们把位置看成点，位置上的数也看成点，把那些不满足条件的关系看做边，那么就成了一个二分图

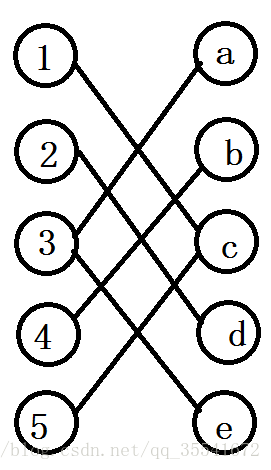
如图是5 2
如果我们把他拉直会怎样

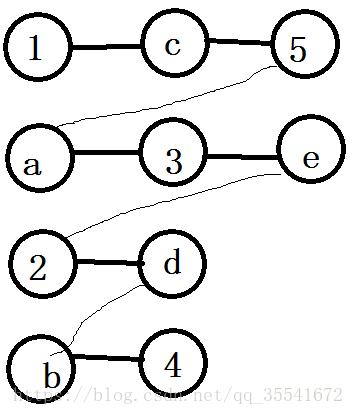
其实就成了几条链
其实也就是说，只有那些%k相同的彼此间会有影响
我们可以通过一个dp，分开计算每条链匹配i条边的方案数，然后再加起来
不过更巧妙的办法是把这些看做一条长链，只是那些原来的链的终止节点不能被匹配，然后答案直接读取末尾的值
也即是说，定义$d(i,j,0/1)$表示前i个，有j个不满足条件，当前节点是否选择
$$d(i+1,j,0)=d(i,j,0)+d(i,j,1)$$
$$d(i+1,j+1,1)=d(i,j,0)$$（注意此处转移时判断是否是两条链的交界处（即是否真的可以连边））
那么，我们要求的f(i)就是$(d(2\ast n,i,0)+d(2\ast n,i,1))\ast (n-i)!$
然后容斥

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int mod=924844033;
const int N=4005;
int n,k;
bool vis[N][2];
bool ed[N];
int tot;
int d[N][N][2];
int f[N];
int fact[N];
int main()
{
    //freopen("captain.in","r",stdin);
    //freopen("captain.out","w",stdout);
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)
        for(int j=0;j<=1;j++)
            if(!vis[i][j]){
                int len=0;
                for(int x=i,y=j;x<=n;x+=k,y^=1)
                    vis[x][y]=1,len++;
                tot+=len;
                ed[tot]=1;
            }
    ed[0]=1;
    d[0][0][0]=1;
    for(int i=0;i<2*n;i++)
        for(int j=0;j<=n;j++){
            d[i+1][j][0]=(d[i][j][0]+d[i][j][1])%mod;
            if(!ed[i])
                d[i+1][j+1][1]=d[i][j][0];
        }
    for(int i=0;i<=n;i++)
        f[i]=(d[2*n][i][0]+d[2*n][i][1])%mod;
    fact[0]=1;
    for(int i=1;i<=n;i++)
        fact[i]=1ll*fact[i-1]*i%mod;
    int ans=0;
    for(int i=0,j=1;i<=n;i++,j=-j)
        ans=((1ll*ans+1ll*j*fact[n-i]*f[i]%mod)%mod+mod)%mod;
    printf("%dn",ans);
}

这里还有$O(NlogN)$的做法

最后

以上就是懵懂日记本为你收集整理的AGC005 D ~K Perm Counting题意题解的全部内容，希望文章能够帮你解决AGC005 D ~K Perm Counting题意题解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。