AGC005 D ~K Perm Counting dp 容斥 二分图

题目链接
洛谷有翻译的题目链接

题意：
给你一个$n$和一个$k$问你有多少个全排列，使得不存在$a[i]-i=k$，模924844033，$n,k<=2000$。

题解：
我们考虑这个模型，我们可以转化成一个二分图，其中我们让二分图上一侧的表示全排列的$n$个数，另一侧表示每个数不能与它匹配的数字，这样对于左侧的一个$x$，我们会将它与右侧的$x+k$和$x-k$两个点连边（如果存在这两个点的话）。这样我们的思路是想用总方案数减去不合法的方案，我们发现我们需要一个容斥，我们设$n$个点有$i$个点不合法的方案数为$f[i]$，那么答案就是${\sum }_{i=0}^n(-1{)}^i\ast (n-i)!\ast f[i]$。那么我们只需要考虑如果求$f[i]$就可以了。

我们把那个二分图的两侧的点都当场一个点，我们会发现可能相互影响的一些点会形成若干条链，这样我们只需要对每条链dp，然后再合并起来就好了。有一种比较省事的合并的写法，就是我们把不是一条链的也看作接起来。用两张别人的图，可能会说明得比较清楚。

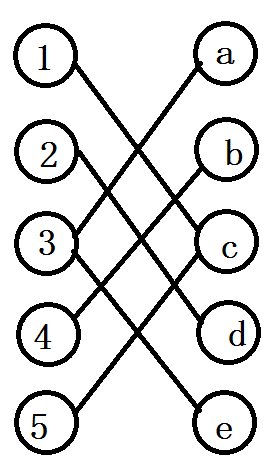
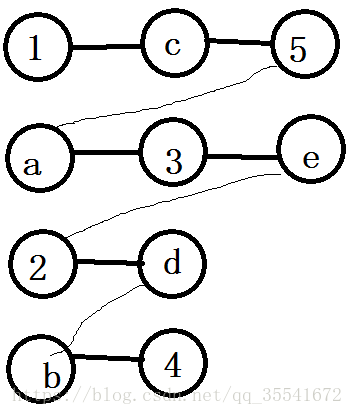
我们考虑dp，我们设$dp[i][j][0/1]$，表示前$i$个位置，有$j$个位置不合法，上一个点与上上个点相连（1）/没有相连（0）的方案数的方案数。我们预处理一下每个点能不能与上一个点相连，这里的不能相连是指把二分图拉成若干条链之后一条链的链首不能与上一条链的链尾相连。转移的话$dp[i][j][0]=dp[i-1][j][0]+dp[i-1][j][1]$，$dp[i][j][1]=dp[i-1][j-1][0]$。算出这个之后就很容易求出结果了。

代码：

#include <bits/stdc++.h>
using namespace std;

int n,k,a[4010],cnt;
long long ans,fac[2010],dp[4010][2010][2];
const long long mod=924844033;
int main()
{
	scanf("%d%d",&n,&k);
	fac[0]=1;
	for(int i=1;i<=n;++i)
	fac[i]=fac[i-1]*i%mod;
	for(int i=1;i<=k;++i)
	{
		for(int l=1;l<=2;++l)//有对称的两条链，举个例子，一个是1->3'->5，一个是1'->3->5' 
		{
			for(int j=i;j<=n;j+=k)
			{
				++cnt;
				if(j!=i)//链头不与前面一个连 
				a[cnt]=1;
			}
		}			
	}
	dp[0][0][0]=1;
	for(int i=0;i<2*n;++i)
	{
		for(int j=0;j<=n;++j)
		{
			dp[i+1][j][0]=(dp[i][j][0]+dp[i][j][1])%mod;
			if(a[i+1])
			dp[i+1][j+1][1]=dp[i][j][0];
		}
	}
	for(int i=0;i<=n;++i)
	{
		if(i&1)
		ans=(ans-(dp[2*n][i][0]+dp[2*n][i][1])*fac[n-i]%mod+mod)%mod;
		else
		ans=(ans+(dp[2*n][i][0]+dp[2*n][i][1])*fac[n-i])%mod;
	}
	printf("%lldn",ans);
	return 0;
}

最后

以上就是大胆月光为你收集整理的AGC005 D ~K Perm Counting dp 容斥 二分图的全部内容，希望文章能够帮你解决AGC005 D ~K Perm Counting dp 容斥 二分图所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。