【题解】[AGC005D] ~K Perm Counting

题意

如果一个排列 $P$ 满足对于所有的 $i$ 都有 $|P_i-i|\ne k$ ，则称排列 $P$ 是合法的。求有多少种合法的排列。

Solution:

本题的限制条件很像错排，但是区别在于并不是一一对应的。

考虑容斥。问题转化成了求满足其中 $K$ 个条件的排列数。

考虑这样一个序列：1 1+k 1+2k ... 1+mk 。在二分图中是这样的：

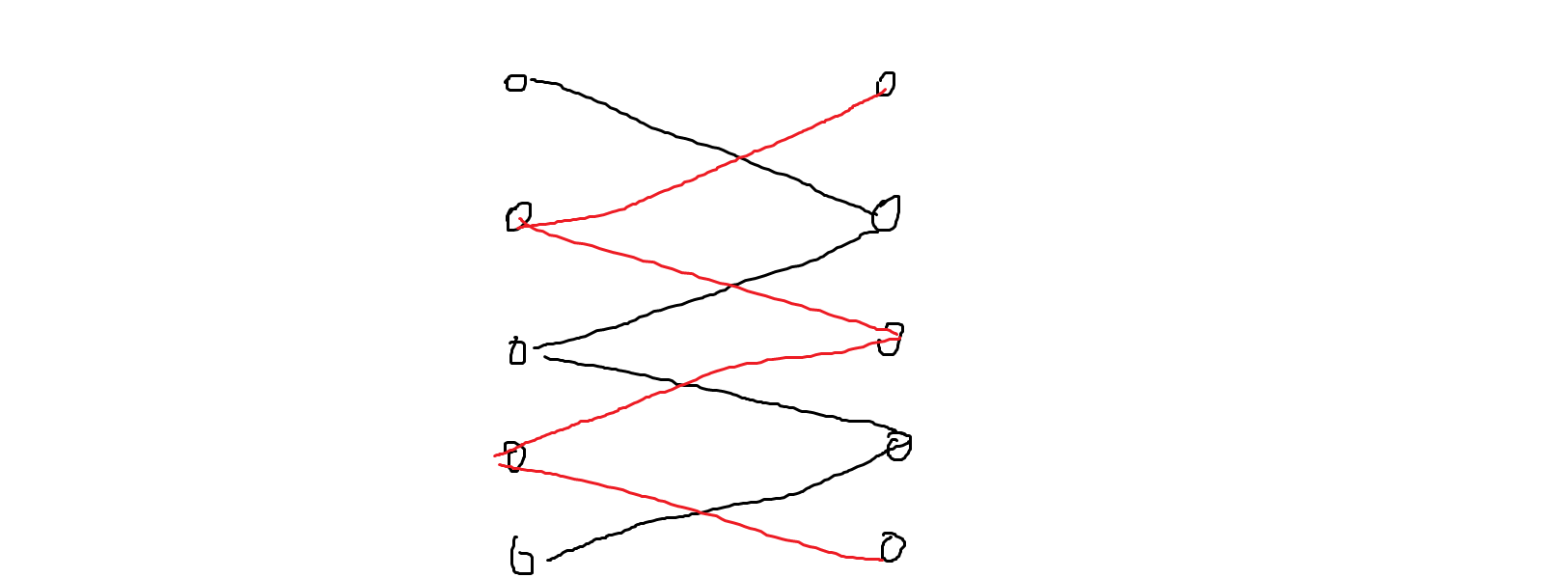
考虑其中一条链。为了使结构统一，我们把原始排列拆分成 $2n$ 个点，这样做的好处是将题意限制转化成了 不能选择两条相邻的边 。（这样点和边形成了映射关系）。

设 $dp[i][j][0/1]$ 表示处理到前 $i$ 个点，其中满足 $j$ 个条件，i->i-1 是否连边。状态转移方程为：

1. $dp[i][j][0]=dp[i-1][j][0]+dp[i-1][j][1]$
2. $dp[i][j][1]=dp[i-1][j-1][0](j>=1)$

当然可以用 背包 将 2k 条链合并。我们可以把 2k 条链合并在一起进行 $dp$ ，对于链首的情况要特殊讨论。

时间复杂度 $O(n^2)$ 。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mod=924844033;
const int mx=4005;
int n,m,k,dp[mx][mx][2],a[mx];
ll res,fac[mx];
int main() {
	scanf("%d%d",&n,&k);
	fac[0]=1; for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%mod;
	for(int i=1;i<=k;i++) {
		for(int j=i;j<=n;j+=k) {
			a[++m]=(j==i);
		}
		for(int j=i;j<=n;j+=k) {
			a[++m]=(j==i);
		}
	}
	dp[0][0][0]=1;
	for(int i=1;i<=m;i++) {
		for(int j=0;j<=i;j++) {
			dp[i][j][0]=(dp[i-1][j][0]+dp[i-1][j][1])%mod;
			dp[i][j][1]=(a[i]==1||j==0)?0:dp[i-1][j-1][0];
		}
	}
	for(int i=0;i<=n;i++) {
		if(i&1) {
			res=(res-1ll*(dp[m][i][0]+dp[m][i][1])*fac[n-i]%mod)%mod;
		}
		else {
			res=(res+1ll*(dp[m][i][0]+dp[m][i][1])*fac[n-i]%mod)%mod;
		}
	}
	if(res<0) res+=mod;
	printf("%lld",res);
} 

最后

以上就是懵懂早晨为你收集整理的【题解】[AGC005D] ~K Perm Counting的全部内容，希望文章能够帮你解决【题解】[AGC005D] ~K Perm Counting所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。