题解-Atcoder_agc005D ~K Perm Counting

Problem

AtCoder-agc005D

题意概要：给出(n,k)，求合法的排列个数，其中合法定义为任何数字所在位置与自身值差的绝对值不为(k)（即求排列({A_i})，使得(forall iin[1,n],|a_i-i|not =k)

Solution

刚看这道题时除了全集取反搞容斥外没有任何思路啊

(f_i)表示排列中至少有(i)对冲突的方案数，一对冲突定义为存在一个(i)使得(|a_i-i|=k)

考虑全集取反，加上一点点容斥思想可得

[Ans=sum_{i=0}^n(-1)^icdot P_n^icdot f_i]

至于怎么得到 (f_i)，就是这道题难点所在，关键思路是画图

构建一个二分图：

• 其中 (i) 为数值 (i)，(i') 为 (i) 在排列中的位置编号
• 构建边为冲突，即所有 (i') 要和 (ipm k) 连边

就像这样（模拟 (n=4,k=1) 的情况）：

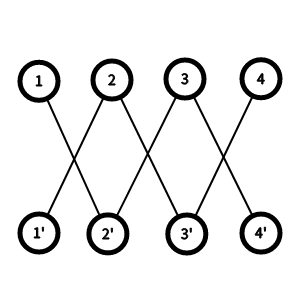
发现这个二分图中其实只有(2k)条链，于是可以对这(2k)条链进行Dp

在某条链上：设(g[i][j][0/1])表示考虑前(i)个点，且已经有(j)对冲突，(i)号与(i+1)号连与不连的方案数，得出转移方程：

[g[i][j][0]=g[i-1][j][0]+g[i-1][j][1]\g[i][j][1]=g[i-1][j-1][0]]

对于每条链的(f[i])即为(g[end][i][0]+g[end][i][1])（(end)为链的末尾），最后合并(2k)条链的时候可以玩背包

但实际上有个小技巧，就是将(2k)条链首尾顺次相接，在两条链的交界处不转移第二个方程即可

Code

#include <cstdio>

const int N=2040,p=924844033;
int f[N+N][N][2];
bool end[N+N];
int n,k,Ans,fac[N];

inline int qm(int x){return x<p?x:x-p;}

int main(){
    scanf("%d%d",&n,&k);fac[0]=1;
    for(int i=1;i<=n;++i)fac[i]=1ll*fac[i-1]*i%p;
    for(int i=1,tt=0,d;i<=k;++i){
        d=(n-i)/k+1;
        tt+=d,end[tt]=true;
        tt+=d,end[tt]=true;
    }
    f[1][0][0]=1;
    for(int i=1;i<=n+n;++i)
    for(int j=0;j<=n;++j){
        f[i+1][j][0]=qm(f[i][j][0]+f[i][j][1]);
        if(!end[i])f[i+1][j+1][1]=f[i][j][0];
    }
    for(int i=0,t;i<=n;++i){
        t=1ll*fac[n-i]*qm(f[n+n][i][0]+f[n+n][i][1])%p;
        if(i&1)Ans=qm(Ans-t+p);
        else Ans=qm(Ans+t);
    }
    printf("%dn",Ans);
    return 0;
}