目录
- 一、题目
- 二、理论基础
- 三、MATLAB代码
一、题目


二、理论基础

三、MATLAB代码
clc;clear;
%输入初值
%像点坐标,单位统一化,以米为单位
imgPt_X=[-86.15,-53.40,-14.78,10.46];
imgPt_Y=[-68.99,82.21,-76.63,64.43];
imgPt_X=imgPt_X/1000;
imgPt_Y=imgPt_Y/1000;
%物方坐标
objPt_X=[36589.41,37631.08,39100.97,40426.54];
objPt_Y=[25273.32,31324.51,24934.98,30319.81];
objPt_Z=[2195.17,728.69,2386.50,757.31];
%比例尺,焦距同一单位为米,旋转矩阵的初始化。
lamda=50000;
f=153.24*0.001;
R=zeros(3);
%初值X0,Y0,Z0,phi0,omega0,kappa0
X0=sum(objPt_X)/4;
Y0=sum(objPt_Y)/4;
Z0=sum(objPt_Z)/4+f*lamda;
%组成外方位元素的初值,External=[△X,△Y,△Z,△φ,△w,△k]
External=[X0,Y0,Z0,0,0,0];
%循环次数
num=0;
%点的个数
i=4;
%像点坐标的近似值
approximate_x=[0];
approximate_y=[0];
%计算L
l=cell(1,4);
value_temp=[];
while 1
%计算旋转矩阵R
R=[cos(External(4)),0,-sin(External(4));0,1,0;sin(External(4)),0,cos(External(4))]*[1,0,0;0,cos(External(5)),-sin(External(5));0,sin(External(5)),cos(External(5))]*[cos(External(6)),-sin(External(6)),0;sin(External(6)),cos(External(6)),0;0,0,1];
%循环计算每个点,当点没有计算完的时候:
while i>0
%共线方程中的Xbar,Ybar,Zbar
X_=R(1,1)*(objPt_X(i)-External(1))+R(2,1)*(objPt_Y(i)-External(2))+R(3,1)*(objPt_Z(i)-External(3));
Y_=R(1,2)*(objPt_X(i)-External(1))+R(2,2)*(objPt_Y(i)-External(2))+R(3,2)*(objPt_Z(i)-External(3));
Z_=R(1,3)*(objPt_X(i)-External(1))+R(2,3)*(objPt_Y(i)-External(2))+R(3,3)*(objPt_Z(i)-External(3));
%根据共线方程求得x,y的近似值(x),(y)
approximate_x(i)=-f*(X_)/(Z_);
approximate_y(i)=-f*(Y_)/(Z_);
%计算Lx=x-(x),Ly=y-(y)
value_temp(1,1)=imgPt_X(i)-approximate_x(i);
value_temp(2,1)=imgPt_Y(i)-approximate_y(i);
l(1,i)={value_temp};
%计算A矩阵:
a11=1/Z_*(R(1,1)*f+R(1,3)*approximate_x(i));
a12=1/Z_*(R(2,1)*f+R(2,3)*approximate_x(i));
a13=1/Z_*(R(3,1)*f+R(3,3)*approximate_x(i));
a21=1/Z_*(R(1,2)*f+R(1,3)*approximate_y(i));
a22=1/Z_*(R(2,2)*f+R(2,3)*approximate_y(i));
a23=1/Z_*(R(3,2)*f+R(3,3)*approximate_y(i));
a14=approximate_y(i)*sin(External(5))-(approximate_x(i)/f*(approximate_x(i)*cos(External(6))-approximate_y(i)*sin(External(6)))+f*cos(External(6)))*cos(External(5));
a15=-f*sin(External(6))-approximate_x(i)/f*(approximate_x(i)*sin(External(6))+approximate_y(i)*cos(External(6)));
a16=approximate_y(i);
a24=-approximate_x(i)*sin(External(5))-(approximate_y(i)/f*(approximate_x(i)*cos(External(6))-approximate_y(i)*sin(External(6)))-f*sin(External(6)))*cos(External(5));
a25=-f*cos(External(6))-approximate_y(i)/f*(approximate_x(i)*sin(External(6))+approximate_y(i)*cos(External(6)));
a26=-approximate_x(i);
%记录每个点的A矩阵,组成单元
A{i}=[a11,a12,a13,a14,a15,a16;a21,a22,a23,a24,a25,a26];
%点的个数减一
i=i-1;
end
%当所有点计算完毕,将A单元cell转换为A_矩阵:
A_=[A{1};A{2};A{3};A{4}];
L=[l{1};l{2};l{3};l{4}];
%计算改正值^x
x=inv(A_'*A_)*A_'*L;
num=num+1;
%改正外方位元素的值:[△X,△Y,△Z,△φ,△w,△k],旧的外方位元素+改正值
External(1:6)=External(1:6)+x(1:6)';
%迭代结束条件,角元素改正值都小于0.000001并且线元素均小于0.01
if abs(x(4))<0.000001&&abs(x(5))<0.000001&&abs(x(6))<0.000001&& abs(x(1))<0.001&&abs(x(2))<0.001&&abs(x(3))<0.001||num>=10
%像点坐标的改正值
V=A_*x-L;
%单位权中误差
sigma0=sqrt(V'*V/(2*4-6));
Q=inv(A_'*A_);
%外方位元素的精度
sigma=Q^0.5*sigma0;
for i=0:3
nimgPt_X(i+1)=(imgPt_X(i+1)+V(2*i+1))*1000;
nimgPt_Y(i+1)=(imgPt_Y(i+1)+V(2*i+2))*1000;
end
break;
end
%继续迭代,将点的个数重新记为4
i=4;
end
%输出结果
disp("外方位元素:");
disp(External);
disp("旋转矩阵R:");
disp(R);
disp("改正后的像X坐标:");
disp(nimgPt_X);
disp("改正后的像Y坐标:");
disp(nimgPt_Y);
disp("单位权中误差:");
disp(sigma0);
disp("外方位元素精度:");
disp(sigma);
参考结果:
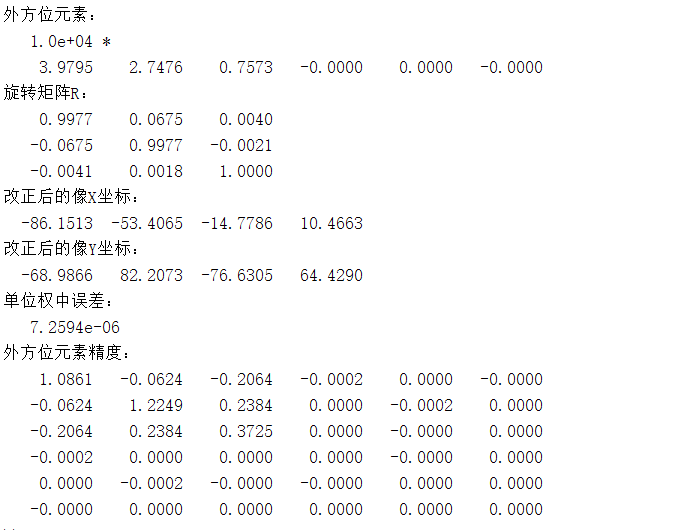

最后
以上就是雪白红酒最近收集整理的关于解析摄影测量之单像空间后方交会(MATLAB)一、题目二、理论基础三、MATLAB代码的全部内容,更多相关解析摄影测量之单像空间后方交会(MATLAB)一、题目二、理论基础三、MATLAB代码内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复