最近用到插值算法,使用三次样条插值时仿真速度太慢,于是采用算法简单的线性插值。本篇主要介绍一下双线性插值的实现方法。
1. 线性插值
已知坐标 (x0, y0) 与 (x1, y1),要得到 [x0, x1] 区间内某一位置 x 在直线上的值。
由于 x 值已知,所以可以从公式得到 y 的值
已知 y 求 x 的过程与以上过程相同,只是 x 与 y 要进行交换。
2. 双线性插值(Bilinear Interpolation)
在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。
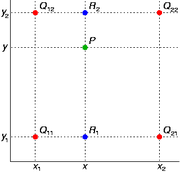
图中:红色的数据点与待插值得到的绿色点
假如我们想得到未知函数 f 在点 P = (x, y) 的值,假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。
首先在 x 方向进行线性插值,得到
然后在 y 方向进行线性插值,得到
这样就得到所要的结果 f(x, y),
双线性插值在三维空间的延伸是三线性插值。
最后
以上就是贤惠寒风最近收集整理的关于双线性插值(Bilinear Interpolation)的全部内容,更多相关双线性插值(Bilinear内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复